Расчет текущей стоимости с многоразовых поступлений от инвестиций

Представим себе следующую ситуацию: имеется некий инвестиционный проект, который требует в первый период времени (год) вложения 125 млн руб., во второй — 150 млн руб., в третий — 160 млн руб. При этом ставки доходности соответственно составляют 25,30 и 40 % годовых. Какую сумму можно инвестировать сейчас в указанный инвестиционный проект?

Задача решается по частям, исходя из требований инвестирования и с учетом ставок доходности:

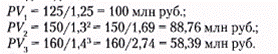
Сложив эти три значения, получим сумму, которую нужно вложить сейчас:

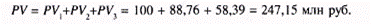
В обобщенном виде формула выглядит так:

где t—номер года, t = 1,..., n; C_t —- поступления t-гo года; E_t — доходность t-гогода. Для закрепления материала предлагаем на основе условий, представленных в табл.П. 1.1. определить сумму вложений в проекты в настоящее время.

Таблица П. 1.1

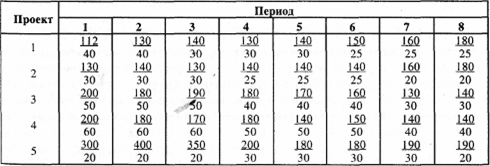
Представьте себе, что вы ограничены в средствах, а потому вынуждены при прочих равных условиях выбирать такой проект, который в настоящее время требует вложить меньше всего средств. Исходя из данных табл. П. 1.1., выявите лучший проект.

Для каждого инвестиционного проекта, предполагающего многоразовые поступления в течение нескольких лет, можно определить структуру ставок доходности.

При этом инвесторы всегда ориентируются на среднерыночные ставки доходности, под которыми понимают уровни доходности от вложений в предприятия определенных отраслей или же процентные ставки для средне- и долгосрочных банковских кредитов. Вот почему такую структуру доходности иногда называют повременной структурой процентных ставок (англ. term structure of interest rates).

Общая структура ставок доходности помогает сопоставить инвестиционные альтернативы. Предположим, есть 7000 млн руб., которые необходимо израсходовать на выполнение некоторого инвестиционного проекта предприятия. Ряд организаций предлагают свои услуги в проектировании и осуществлении инвестиционных проектов. Поскольку все проекты имеют одинаковую направленность и различаются лишь незначительными особенностями, нам нужно выбрать наиболее приемлемый для инвестирования проект, допустив, что степень риска и прочие условия одинаковы.

Исходные данные приведены в табл. П.1.2.

Таблица П. 1.2

Проект	Поступления в n-м году «Cn», млн руб.
n = 1	n = 2	n = 3	n = 4	n = 5
А	—
Б					—
В
Г			—
Ставка доходности, %

Для поиска наилучшего решения используем формулу (П.1.9):

Тогда:

Результаты вычислений свидетельствуют, что при использовании средних рыночных ставкок в проект А следует инвестировать не более 6684,4 млн руб., в проект Б — не более 8162,5 млн руб., в проект В — не более 6416 млн руб., в проект Г — не более 8622,3 млн руб. Если мы вложим в каждый из проектов по 7000 млн руб., то проект А принесет убыток 315,6 млн руб.; проект Б даст экономию 1162,5 млн руб., проект В нанесет ущерб в размере 584 млн руб., проект Г сэкономит 1622,3 млн руб. Следовательно, проекты Б и Г предлагают инвестиционные решения, которые выгоднее рыночных, а проекты А и В — хуже рыночных.

Основываясь на изложенных выше посылках, оцените выгодность вариантов вложения 8000 млн руб. в проекты, характеризуемые данными табл. П.1.3—П.1.5.

Таблица П. 1.3

Проект	Сn , млн руб.
	п = 1	п = 2	п = 3	п =4	п = 5
А Б В		-			-
Ставка доходности, %

Таблица П. 1.4

Проект	Cn , млн руб.
	п = 1	п = 2	n =3	п =4	п = 5	n = 6
А	—
Б						—
В						—
Ставка доходности, %

Таблица П. 1.5

Проект	Сn , млн руб.
	п = 1	n = 2	п = 3	n = 4	n = 5
А Б В Г	- -				-
Ставка доходности, %

На практике при анализе различных типов инвестиций приходится рассматривать многократные поступления, связанные с поэтапной оплатой работ (проектно-исследовательских и опытно-конструкторских работ, установки оборудования и др.).

В этом случае порой возникают затруднения с определением текущей цены инвестиционного проекта. Как правило, задачи подобного типа решаются путем приведения инвестиций, осуществляемых в будущих периодах, к настоящему моменту времени, исходя из ставки доходности за тот год, в котором они производятся.

Например, имеется некий инвестиционный проект, требующий первоначального взноса в размере 100 млн руб. и повторного (через год) в размере 200 млн руб. Лишь затем последуют поступления: через два года 300 млн руб., а на третий — 100 млн руб. Выгоден ли проект, если структура доходности такова: 1-й год — 10%, 2-й - 15 %, 3-й - 20 %?

Рассмотрим дисконтированную стоимость проекта. По сути, мы определяем стоимость инвестиций, которые необходимо осуществить сегодня, вместо того чтобы вкладывать средства в соответствующем году. Решение задачи сводится к нахождению

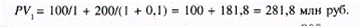
Это значит, что инвестируемые в соответствующие годы 300 млн руб. «стоят» сейчас только 281,8 млн руб. При этом первоначальный взнос тоже как бы дисконтируется, но с коэффициентом, равным 1.

Определим уже известным способом текущую стоимость будущих поступлений (доход) от реализации проекта:

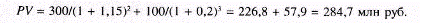
Следовательно, для реализации проекта необходимо сейчас вложить 281,8 млн руб. и получить 284,7 млн руб. Отсюда разница между текущей дисконтированной стоимостью и необходимыми для его реализации вложениями составляет

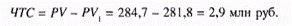
Итак, мы получим чистую текущую стоимость проекта, которая определяется путем вычета суммы первоначальных инвестиций в проект из текущей стоимости проекта. Исчисленное значение больше нуля, значит, данный проект более выгоден, чем инвестиции на среднерыночных условиях. Если бы значение ЧТС оказалось меньше нуля, то он был бы менее выгодным.

Для закрепления полученных знаний предлагаем решить ряд задач по оценке эффективности вложений, условия которых приведены в табл. П.1.6-П.1.9.

Таблица П. 1.6

Показатель	Шаг расчета t
Объем вложений, млн руб.				—	—	—
Сn, млн руб.	—	—	—
E, %	—

Таблица П. 1.7

Показатель	Шаг расчета t
Объем вложений, млн руб.					—	—	—
Cn, млн руб.	—	—	—
Е,%	—

Таблица П. 1.8

Показатель	Шаг расчета t
Объем вложений, млн руб.					—	—	—	—
Сn, млн руб.	—	—	—	—
E, %	—

Таблица П. 1.9