Алгоритм отсечения многоугольников

Вейлера-Азертона

В отличие от других алгоритмов алгоритм Вейлера-Азертона позволяет отсекать невыпуклые многоугольники с отверстиями по другим невыпуклым многоугольникам с отверстиями, причем одновременно возможно как внутреннее, так и внешнее отсе-чение.

Как обрабатываемый, так и отсекающий многоугольники описываются в алгоритме циклическими списками вершин. Внешняя граница каждого многоугольника обходится по часовой стрелке, а внутренняя (или отверстия) – против часовой стрелки (для того, чтобы отсекаемая область была всегда справа). Границы обрабатываемого и отсекающего многоугольников могут пересекаться или не пересекаться. Если они пересекаются, то они образуют пары – одно из пересечений – когда ребро обрабатываемого многоугольника входит внутрь отсекающего, а другое – когда выходит. При этом точки пересечения заносятся в циклические списки вершин.

Алгоритм начинается с точки пересечения входного типа, затем он прослеживает внешнюю границу до тех пор, пока не обнаружится еще одно пересечение. В точке пересечения производится поворот "направо" и т.д., пока не встретится начальная точка пересечения. Внутренние границы обрабатываемого многоугольника обходятся против часовой стрелки.

Формальная запись алгоритма:

– вычислить все точки пересечения обрабатываемого и отсекающего многоугольников;

– добавить эти точки пересечения к циклическим спискам вершин многоугольников;

– создать 4 списка: 2 списка вершин многоугольников и 2 списка для входящих и выходящих точек пересечения;

– взять точку из списка входящих пересечений;

– просматривать список вершин обрабатываемого многоугольника, пока не обнаружится следующая точка пересечения (при этом не забывать переносить координаты "проходимых" вершин и точек пересечения в результирующий список);

– используя двухстороннюю связь, перейти к списку вершин отсекающего многоугольника;

– повторять, пока не будет достигнута начальная точка пересечения;

– изобразить полученный результат;

– если в списке входящих пересечений пройдены не все точки, то взять следующую точку пересечения и повторить алгоритм сначала.

Для поиска внешнего отсечения начальная точка берется из списка выходящих пересечений, а вершины из списка вершин отсекателя просматриваются в обратном порядке.

Для наглядности приведем несколько примеров. Будем обозначать вершины отсекаемого многоугольника как S_i, отсекателя как C_i, а точки пересечения как I_i. Тогда для рис. 7.5 список пересечений входного типа: I₂, I₄, I₆, а список пересечений выходного типа: I₁, I₃, I₅.

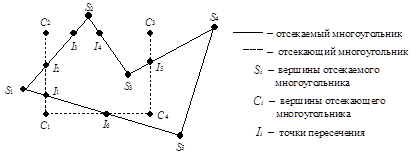
Рис. 7.5. Пример простого отсечения

Для внутреннего отсечения циклические списки вершин и порядок работы представлены на рис. 7.6.

Начинаем с точки пересечения входного типа I₂. Далее движемся вниз, находим следующую точку пересечения и переходим в другой список и т.д. При этом не забываем записывать "пройденные" вершины в результат:

I₂, I₃, I₄, S₃, I₅, C₄, I₆, I₁, I₂.

Кроме того, вычеркиваем из списка пересечений входного типа уже пройденные точки. Если точек в этом списке больше нет, то алгоритм закончен.

Для поиска внешнего отсечения берем вершину из списка выходящих вершин и далее действуем согласно алгоритму, но не забываем, что список вершин отсекателя проходится уже снизу вверх (рис. 7.7).

В результате получаем 3 многоугольника:

I₁, S₁, I₂, I₁;

I₃, S₂, I₄, I₃;

I₅, S₄, S₅, I₆, C₄, I₅.

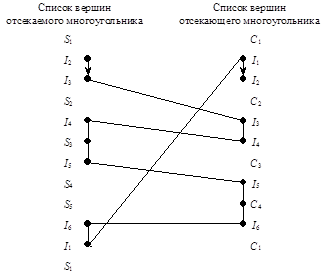
Рис. 7.6. Внутреннее отсечение многоугольника на рис. 7.5

Рис. 7.7. Внешнее отсечение многоугольника на рис. 7.5

Приведем более сложный пример, когда и отсекаемый и отсекающий многоугольники имеют отверстия (не забываем, что обход отверстий идет против часовой стрелки). Кроме того, у нас в циклическом списке вершин появляется несколько (в зависимости от количества отверстий) "контуров" (рис. 7.8).

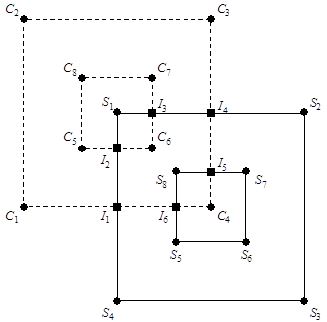
Рис. 7.8. Пример отсечения многоугольников с отверстиями

Список пересечений входного типа: I₁, I₃, I₅, а список пересечений выходного типа: I₂, I₄, I₆.

Для внутреннего отсечения получаем многоугольник (рис. 7.9):

I₁, I₂, C₆, I₃, I₄, I₅ S₈, I₆, I₁.

Для внешнего отсечения получаем многоугольники (рис .7.10):

I₂, S₁, I₃, C₆, I₂ и I₄, S₂, S₃, S₄, I₁, I₆, S₅, S₆, S₇, I₅, I₄.

Для корректной работы необходимо аккуратно классифицировать и вычислять точки пересечения. Касание со стороной отсекателя не считается пересечением (рис. 7.11).

Рис. 7.9. Внутреннее отсечение многоугольника на рис. 7.8

Рис. 7.10. Внешнее отсечение многоугольника на рис. 7.8

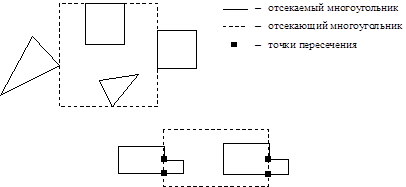
Рис. 7.11. Корректное определение точек пересечения

Задание на лабораторную работу № 7
"Алгоритмы отсечения многоугольников"

1. Построить отсекаемый многоугольник (цвет 1).

2. Построить отсекающий многоугольник (цвет 2).

3. Выделить цветом область отсечения (цвет 3).

4. Повторить для всех вариантов расположения многоуголь-ников:

– отсекаемый многоугольник вне отсекающего многоугольника;

– отсекаемый многоугольник внутри отсекающего многоугольника;

– отсекаемый многоугольник пересекает отсекающий многоугольник и т.д. (в том числе различные варианты пересечения отверстий).

Сравните два алгоритма. Отметьте преимущества и недостатки.

Заключение

В данном учебном пособии были рассмотрены основные алгоритмы компьютерной графики, без которых было бы невозможно написание таких программ, как WinWord, CorelDraw и Acrobat Reader.

Список используемой литературы очень обширен, а конкретная реализация алгоритма зависит только от квалификации программиста, но приведем основные источники, которыми пользовались авторы при написании данного пособия.

Литература

1. Роджерс Д. Алгоритмические основы машинной графики: Пер. с англ. – М.: Мир, 1989.

2. Вельтмандер П.В. Алгоритмы компьютерной графики: http: // ermak. cs.nstu.ru/kg_rivs

3. D. Hearn, P. Baker, Computer Graphics: Prentice Hall, Inc., Englewood Cliffs, New Jersey, 1994.

оглавление

Стр.

1. Генерация векторов...................................................... 3

1.1. Цифровой дифференциальный анализатор (ЦДА)......... 4

1.2. Алгоритм Брезенхема..................................................... 6

Задание на лабораторную работу № 1 "Генерация

векторов".......................................................................... 9

2. Фильтрация. Модифицированный алгоритм

Брезенхема....................................................................... 10

2.1. Модифицированный алгоритм Брезенхема.................. 10

2.2. Улучшение качества изображения фильтрацией......... 12

Задание на лабораторную работу № 2 "Фильтрация.

Модифицированный алгоритм Брезенхема "............... 14

3. Алгоритмы генерации окружности..................... 15

3.1. Целочисленный алгоритм Брезенхема......................... 16

3.2. Алгоритм Мичнера для построения окружности........ 20

Задание на лабораторную работу № 3 "Алгоритмы

генерации окружности"................................................. 20

4. Алгоритмы построчного заполнения

многоугольников........................................................ 21

Задание на лабораторную работу № 4 "Алгоритмы

построчного заполнения многоугольников"................. 23

5. Заливка области с затравкой................................ 25

5.1. Заливка области с затравкой......................................... 25

5.2. Простой алгоритм заливки............................................ 27

5.3 Построчный алгоритм заливки с затравкой.................. 28

Задание на лабораторную работу № 5 "Заливка области

с затравкой ".................................................................... 28

6. Алгоритмы отсечения отрезков............................ 29

6.1. Двумерный алгоритм Коэна-Сазерленда...................... 29

6.2. Двумерный FC-алгоритм............................................... 30

6.3. Алгоритм Кируса-Бека.................................................. 33

6.3.1. Определение факта выпуклости многоугольника 36

6.3.2. Вычисление уравнения внутренней нормали..... 38

Задание на лабораторную работу № 6 "Алгоритмы

отсечения отрезков"...................................................... 40

7. Алгоритмы отсечения многоугольников............................. 41

7.1. Алгоритм Сазерленда-Ходжмена................................. 41

7.2. Алгоритм отсечения многоугольников

Вейлера-Азертона.......................................................... 44

Задание на лабораторную работу № 7 "Алгоритмы

отсечения многоугольников"....................................... 51

Заключение......................................................................... 52

Литература........................................................................... 52