Изображение многоугольников и многогранников

1. Изображение фигуры. Выберем некоторую плоскость p и назовем ее плоскостью изображений. Затем возьмем прямую l, пересекающую плоскость p, и спроектируем данную фигуру 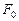(плоскую или пространственную) на плоскость p параллельно прямой l. Полученную плоскую фигуру F¢ (проекцию фигуры 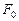) или любую подобную ей фигуру F на плоскости p будем называть изображением фигуры .

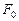Возникает вопрос, почему изображением фигуры принято считать не только ее проекцию, но любую фигуру, подобную этой проекции. Дело в том, что в реальной практике плоскостью изображений является плоскость листа бумаги или, например, плоскость классной доски. Бывает так, что проекция фигуры-оригинала не помещается на этом листе или доске. Наоборот, если фигура-оригинал достаточно мала, то малые размеры имеет и ее проекция, – с таким изображением также неудобно работать. Кроме того, проекция на плоскости изображения может оказаться неудобно расположенной. Во всех этих случаях и выручает преобразование подобия, которому подвергают проекцию.

Таким образом, при изображении фигур мы сталкиваемся с определенным произволом. Это выбор плоскости изображений, выбор направления проектирования и выбор подобия на плоскости изображений. Удачным считается такой выбор, при котором изображение является наглядным, удачно расположено и имеет удобные для работы размеры.

2. Изображение плоских многоугольников. Будем предполагать, что плоскость многоугольника не совпадает с плоскостью изображения и не является ей параллельной.

Теорема 1. Изображением данного треугольника (в частности, равностороннего или равнобедренного) является произвольный треугольник.

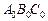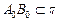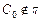Доказательство. Пусть – произвольный треугольник, расположенный в пространстве. Выберем плоскость изображения p так, чтобы и (рис. 13). Возьмем в плоскости p произвольный треугольник АВС и покажем, что его можно принять за изображение треугольника 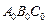. Для этого на отрезке 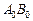, как на стороне, построим в плоскости p треугольник 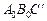, подобный треугольнику АВС. Треугольник 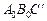является проекцией треугольника 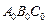на плоскость p параллельно прямой 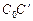. Поэтому треугольник , а значит и подобный ему треугольник , будут являться изображениями треугольника . ■

Следствие. Изображением данного параллелограмма (в

частности, прямоугольника, квадрата и ромба) является произвольный параллелограмм.

Действительно, пусть 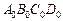– данный параллелограмм и 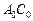– его диагональ, а АВСD – произвольный параллелограмм на плоскости изображений p (рис. 14). Треугольник АВС, согласно доказанного выше, можно принять за изображение треугольника 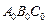. Так как при параллельном проектировании и подобии параллельные прямые переходят в параллельные, параллелограмм АВСD будет изображением параллелограмма .

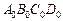Теорема 2. Если дано изображение треугольника 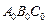, то можно построить изображение любой точки, принадлежащей плоскости этого треугольника.

Доказательство. Пусть АВС – изображение треугольника 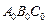и 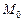– произвольная точка в плоскости треугольника 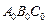(рис. 15). Если через точку 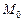и вершины треугольника 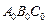провести прямые, то хотя бы одна из них пересекает прямую, содержащую соответствующую противоположную сторону треугольника. Пусть, например, прямая 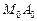пересекает прямую 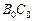в точке 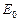. Поскольку при параллельном проектировании и подобии сохраняется отношение трех точек прямой, то изображение Е точки 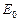можно построить. Точка Е делит отрезок ВС в том же отношении, в каком делит отрезок 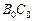точка 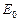: 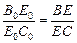. При этом точка Е лежит между точками В и С, если точка 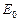лежит между точками В₀ и С₀, а если точка 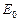лежит вне отрезка В₀С₀, то точка Е также лежит вне отрезка ВС.

Точка М должна лежать на прямой АЕ, а ее положение на этой прямой определяется соотношением: 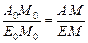. Найденными двумя пропорциями точка 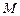однозначно определяется. ■

Опираясь на теорему 2, можно построить изображение любого многоугольника.

Слева на рис. 16 дан выпуклый пятиугольник А₀В₀С₀D₀E₀. Справа выполнено его изображение. Сделайте соответствующие пояснения.

Рис. 16

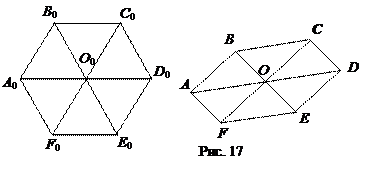Изображения некоторых многоугольников удается выполнить более просто, не прибегая к теореме 2. Рассмотрим, например, построение изображения правильного шестиугольника (рис. 17).

Центр О₀ правильного шестиугольника является серединой его диагоналей A₀D₀, B₀E₀ и C₀F₀, а четырехугольник A₀B₀C₀О₀является параллелограммом. За изображение этого параллелограмма можно принять любой параллелограмм ABCO. Вершина О параллелограмма ABCO будет серединой диагоналей AD, BE и CF, шестиугольника-изображения.

Примечание. При выполнении изображений на практике оригинал можно не строить. Здесь он дан лишь для объяснения способа построения изображения.

3. Изображение тетраэдра. При изображении плоских многоугольников основополагающую роль играет изображение треугольника. Естественно ожидать, что аналогичную роль при изображении многогранников будет выполнять изображение тетраэдра. Оказывается, это действительно так. Справедлива теорема Польке-Шварца, которую мы приводим без доказательства. Эту теорему в 1864 г. доказал немецкий геометр Карл Шварц, а ранее в 1853 г. ее частный случай рассмотрел Польке.

Теорема (Польке-Шварца). Изображением данного тетраэдра является всякий четырехугольник вместе с его диагоналями (рис. 18).

Эта теорема, конечно, дается в предположении, что ни одна из граней тетраэдра не параллельна направлению проектирования.

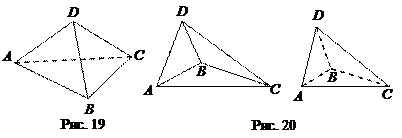
Заметим также, что четырехугольник, о котором идет речь в теореме, не обязательно является выпуклым. Так, на рис. 19 четырехугольник ABCD – выпуклый, а на рис. 20 – невыпуклый. Для большей наглядности на этих рисунках невидимые с точки зрения наблюдателя ребра изображены пунктирными линиями.

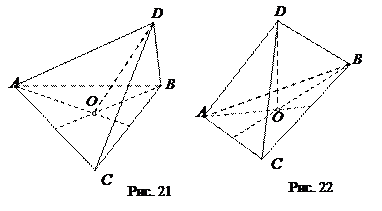Заботясь о наглядности, при выполнении изображений тетраэдра часто приходится учитывать его вид. Рассмотрим, например, изображение правильной треугольной пирамиды. Основание высоты, опущенной из вершины такой пирамиды, совпадает с центром правильного треугольника, лежащего в основании. Поэтому изображение правильной пирамиды и ее высоты может быть таким, каким дано на рис. 21. Однако в этом случае изображение не будет наглядным. Дело в том, что наш опыт зрительного восприятия окружающих предметов основан на том, что, как правило, эти предметы установлены на горизонтальной плоскости, а плоскость изображения параллельна линии тела, т.е. является вертикальной. Ясно, что при этом вертикальные отрезки проектируются на плоскость изображений в вертикальные. В школьной практике мы также считаем, что геометрические тела расположены на горизонтальной плоскости, а плоскость чертежа принимаем за вертикальную. Поэтому на чертеже высоту правильной пирамиды изображают вертикальным отрезком (рис. 22). Такое изображение правильной треугольной пирамиды, естественно, является более наглядным.

Аналогичная ситуация возникает при изображении тетраэдра, у которого одно из ребер перпендикулярно основанию. Любой из четырехугольников на рисунках 19, 20 является изображением этого тетраэдра, но более наглядными будут изо

бражения на рисунках 23.

4. Изображение произвольной пирамиды. Изображением n-угольной пирамиды является фигура, состоящая из
n-угольника, изображающего основание пирамиды, и n треугольников с общей вершиной, изображающих ее боковые грани.

При построении изображений конкретной пирамиды приходится использовать не только теорему Польке-Шварца, но и правила изображения плоских многоугольников. Рассмотрим в качестве примера изображение правильной шестиугольной пирамиды и ее высоты. Прежде всего, заметим, что для того, чтобы изображение было наглядным, как и в случае тетраэдра, направление проектирования не должно быть параллельным ни одной из граней пирамиды.

В основании правильной шестиугольной пирамиды лежит правильный шестиугольник. Его изображение было рассмотрено в пункте 2. Так как высота правильной пирамиды перпендикулярна ее основанию, а основание высоты совпадает с центром правильного многоугольника, лежащего в основании, то высота пирамиды изобразится вертикальным отрезком OS (рис. 24). Отрезки, соединяющие точку S с вершинами шестиугольника, будут изображать боковые ребра пирамиды. По теореме Польке-Шварца четырехугольник OABS вместе с его диагоналями является изображением тетраэдра, вершинами которого будут: вершина пирамиды, две смежные вершины основания и его центр. Поскольку остальные вершины основания строятся с учетом правил изображения плоских многоугольников, то построенная фигура будет действительно изображением правильной шестиугольной пирамиды и ее высоты.

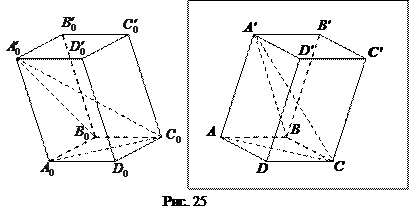
5. Изображение параллелепипеда. Изображением параллелепипеда, в частности, прямоугольного параллелепипеда и куба, является фигура, состоящая из трех пар попарно равных параллелограммов. При этом в каждой паре один параллелограмм получается из другого параллельным переносом.

В параллелепипеде-оригинале 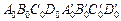вершины, 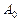, , 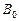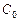и 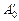являются вершинами тетраэдра (рис. 25). По теореме Польке-Шварца изображением вершин тетраэдра служат вершины произвольного четырехугольника 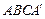. Изображения остальных вершин параллелепипеда строятся с учетом того, что изображениями его противоположных граней будут попарно равные параллелограммы.

Задача. На рис. 26 даны параллельные проекции параллелепипеда на плоскость. Как должна быть расположена прямая, задающая направление проектирования, по отношению к граням параллелепипеда, чтобы получились эти проекции?

Заметим, что изображения, полученные на основе проекций, данных на рис. 26, не являются наглядными.

Согласно сказанному выше, фигура на рис. 25 может служить как изображением произвольного параллелепипеда, так и изображением прямоугольного параллелепипеда (в частности, куба). Догадаться по такому изображению о том, что на нем изображен прямоугольный параллелепипед невозможно, и, кроме того, такое изображение не соответствует нашему зрительному опыту. Так как боковые ребра прямоугольного параллелепипеда перпендикулярны его основаниям, то нам более привычно видеть их изображения в виде вертикальных отрезков. Более того, если плоскость изображения выбрать параллельной некоторой паре противоположных граней параллелепипеда, то проекции выбранных граней будут равны самим граням.

Такие проекции прямоугольного параллелепипеда и куба даны на рис. 27. Фигуры на этих рисунках, а также фигуры, подобные им, мы и договоримся выполнять, когда необходимо построить изображения прямоугольного параллелепипеда и куба.

6. Изображение призмы. Изображением n-угольной призмы является фигура, состоящая из двух равных
n-угольников, один из которых получается параллельным переносом из другого, и n параллелограммов. При этом стороны этих параллелограммов, соединяющие соответствующие вершины n-угольников, параллельны (рис. 28, ).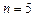

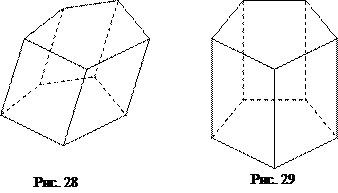При изображении прямой призмы естественно вновь отрезки, изображающие боковые ребра, выбрать вертикальными (рис. 29, ).