Нарезание зубьев со смещением
(корригирование).
 Корригирование зубчатых зацеплений представляет собой улучшение свойств зацеплений путем очерчивания рабочего профиля зубьев различными участками эвольвенты той же окружности (рис. 5.3). Это достигается смещением инструмента при нарезании зубьев. Начальная и делительная плоскости могут совпадать (1) и не совпадать (2). Если эти плоскости совпадают, то расстояние от оси зубчатого колеса до делительной плоскости рейки
Корригирование зубчатых зацеплений представляет собой улучшение свойств зацеплений путем очерчивания рабочего профиля зубьев различными участками эвольвенты той же окружности (рис. 5.3). Это достигается смещением инструмента при нарезании зубьев. Начальная и делительная плоскости могут совпадать (1) и не совпадать (2). Если эти плоскости совпадают, то расстояние от оси зубчатого колеса до делительной плоскости рейки
E1 = 0,5d = 0,5mz.
Расстояние между начальной и делительной плоскостями инструментальной рейки называется смещением исходного контура
X = E2 -E1 = E2 - 0,5d.
Отношение 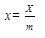 называется коэффициентом смещения исходного контура.
называется коэффициентом смещения исходного контура.
 Корригированием можно поднять несущую способность передач вследствие утолщения зуба у основания, возможности уменьшения числа зубьев и соответственно увеличения модуля, увеличения радиусов кривизны эвольвентного профиля. Корригирование устраняет подрезание зубьев при их изготовлении и позволяет вписывать передачу в заданное межосевое расстояние. Коррекция зацепления может быть высотной и угловой. При высотной коррекции колесо нарезают с отрицательным смещением производящей рейки равным по абсолютной величине положительному смещению производящей рейки шестерни.
Корригированием можно поднять несущую способность передач вследствие утолщения зуба у основания, возможности уменьшения числа зубьев и соответственно увеличения модуля, увеличения радиусов кривизны эвольвентного профиля. Корригирование устраняет подрезание зубьев при их изготовлении и позволяет вписывать передачу в заданное межосевое расстояние. Коррекция зацепления может быть высотной и угловой. При высотной коррекции колесо нарезают с отрицательным смещением производящей рейки равным по абсолютной величине положительному смещению производящей рейки шестерни.
Таким образом, x2 = -x1 и
xå = x1+x2 = 0.
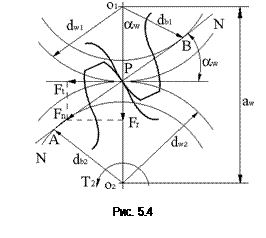
При этом толщина зуба шестерни по делительной окружности увеличивается, а толщина зуба колеса уменьшается, но суммарная их толщина остается постоянной. При угловой коррекции xå=x1+x2>0 и сумма толщин зубьев по делительной окружности обычно больше, чем у некорригированных колес, поэтому оси колес приходится раздвигать, начальные окружности не совпадают с делительными и угол зацепления увеличен (рис. 5.4). Межосевое расстояние
aw=0,5 (dw2±dw1).
Делительное межосевое расстояние
a=0,5(d2±d1).
При отсутствии коррекции, если a=aw, то a=aw,где a- угол профиля производящей рейки.
В соответствии с ГОСТ 13755-81 a=20°. Увеличение a приводит к увеличению толщины зуба у основания, а следовательно, и к увеличению его прочности. Поэтому в авиации применяют a=22°; 25°;28°; 30°.
db=dw×cosaw и db=d×cosa, отсюда cosaw= 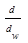 cosa=
cosa=  cosa.
cosa.
 Изменение межосевого расстояния при эвольвентных профилях не равно сумме смещений колес и оценивается коэффициентом воспринимаемого смещения
Изменение межосевого расстояния при эвольвентных профилях не равно сумме смещений колес и оценивается коэффициентом воспринимаемого смещения 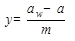 . В этом случае разность суммарного коэффициента смещения xå и коэффициента воспринимаемого смещения определяют значение коэффициента уравнительного смещения Dy=xå - y. Изменением на величину Dу диаметров вершин колес удается сохранить неизменным стандартный радиальный зазор в зацеплении, который равен с=0,25m. В этом случае
. В этом случае разность суммарного коэффициента смещения xå и коэффициента воспринимаемого смещения определяют значение коэффициента уравнительного смещения Dy=xå - y. Изменением на величину Dу диаметров вершин колес удается сохранить неизменным стандартный радиальный зазор в зацеплении, который равен с=0,25m. В этом случае
da=d+2 (1+x-Dy)m; df=d-2(1,25-x)m;
aw=0,5 (dw2±dw1)= 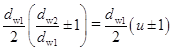 .
.
Усилия в зацеплении
Необходимо определить усилия, действующие в зацеплении. Т2 –момент сопротивления на колесе, который должен быть преодолен моментом Т1 на шестерне.  - нормальная сила, направленная по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. Силу Fn раскладывают на окружную Ft и радиальную Fr.
- нормальная сила, направленная по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. Силу Fn раскладывают на окружную Ft и радиальную Fr.

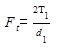 и через Ft выражаем другие составляющие
и через Ft выражаем другие составляющие
Fr=Ft tgaw ;  .
.
Расчетная нагрузка
Полная нагрузка, в дальнейшем именуемая расчетной, слагается из номинальной и динамической нагрузок. Номинальная нагрузка действует на зубья в связи с передачей крутящего момента от шестерни к колесу и определяется наибольшим длительно действующим крутящим моментом Т1 на шестерне.
Динамическая нагрузка возникает из-за того, что нарушается правильное зацепление зубьев. Расчетная нагрузка определяется как произведение номинальной нагрузки на коэффициент нагрузки Fp=Fnk. Коэффициент нагрузки удобно представить как произведение двух коэффициентов:
k=kb kv,
где kb - коэффициент концентрации нагрузки; kv - коэффициент динамичности нагрузки.
Для предварительных расчетов можно взять k=1,3¸1,5.
 Коэффициент концентрации нагрузки kb .Неравномерность распределения нагрузки по ширине колеса связана с деформацией валов, корпусов, опор и самих зубчатых колес. Под действием радиальной нагрузки Fr валы прогнутся (рис. 5.6). Угол перекоса g определяется как сумма углов перекоса шестерни и колеса. Такого перекоса не происходит, если колеса расположены симметрично относительно опор.
Коэффициент концентрации нагрузки kb .Неравномерность распределения нагрузки по ширине колеса связана с деформацией валов, корпусов, опор и самих зубчатых колес. Под действием радиальной нагрузки Fr валы прогнутся (рис. 5.6). Угол перекоса g определяется как сумма углов перекоса шестерни и колеса. Такого перекоса не происходит, если колеса расположены симметрично относительно опор.
 Из-за перекоса колес нагрузка по длине зуба распределяется неравномерно, что характеризуется коэффициентом kb°=
Из-за перекоса колес нагрузка по длине зуба распределяется неравномерно, что характеризуется коэффициентом kb°= 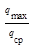 (рис. 5.7), который определяется без учета приработки зубьев.
(рис. 5.7), который определяется без учета приработки зубьев.
Этот коэффициент зависит от:
1) расположения колес между опорами;
2) длины зуба;
3) жесткости валов;
4) конструкции валов.
В ответственных передачах kb° рассчитывают. В приближенных расчетах определяют по графикам и таблицам. При HB>350 kb= kb°. Если HB<350, зубья могут прирабатываться, что снижает неравномерность нагрузки. В этом случае kb=0,5 (1+ kb°).
Для снижения неравномерности распределения нагрузки необходимо:
1. Увеличивать жесткость валов;
2. Опоры располагать симметрично;
3. Применять бомбинированный зуб в сечении а-а (рис.5.8).

 Коэффициент динамичности нагрузки. Неизбежные ошибки в изготовлении и сборке зубчатых колес, а также упругие перемещения зубьев под нагрузкой приводят к тому, что при равномерном вращении шестерни колесо вращается неравномерно. Это приводит к динамическим нагрузкам на зубья и к работе передачи с вибрациями и шумом. Существует 12 степеней точности (чем меньше число, тем точнее передача). Они учитывают кинематическую точность, плавность работы, вид контакта зубьев и боковой зазор. В машиностроении используются степени точности от 9 до 5. Основные динамические нагрузки в прямозубых колесах возникают при входе зубьев в зацепление и при выходе из зацепления предшествующей пары зубьев. Для безударной работы в первую очередь необходимо, чтобы зубья входили в зацепление и выходили из него по линии зацепления, т.е. чтобы были равны основные шаги под нагрузкой.
Коэффициент динамичности нагрузки. Неизбежные ошибки в изготовлении и сборке зубчатых колес, а также упругие перемещения зубьев под нагрузкой приводят к тому, что при равномерном вращении шестерни колесо вращается неравномерно. Это приводит к динамическим нагрузкам на зубья и к работе передачи с вибрациями и шумом. Существует 12 степеней точности (чем меньше число, тем точнее передача). Они учитывают кинематическую точность, плавность работы, вид контакта зубьев и боковой зазор. В машиностроении используются степени точности от 9 до 5. Основные динамические нагрузки в прямозубых колесах возникают при входе зубьев в зацепление и при выходе из зацепления предшествующей пары зубьев. Для безударной работы в первую очередь необходимо, чтобы зубья входили в зацепление и выходили из него по линии зацепления, т.е. чтобы были равны основные шаги под нагрузкой.
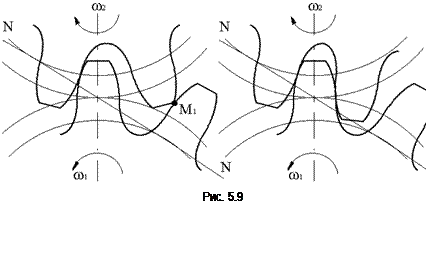
Наблюдаются удары двух основных видов - кромочный и срединный.
Если основной шаг ведомого колеса 2 больше, чем шаг ведущего 1 (Рb2>Pb1) (рис. 5.9, а), то происходит преждевременный вход в зацепление кромки ведомого колеса (в т. М, а не на линии зацепления) и так называемый кромочный удар. Если основной шаг ведомого колеса меньше, чем шаг ведущего (Рb2<Pb1), то происходит запаздывание выхода из зацепления предшествующей пары зубьев и так называемый срединный удар последующей пары зубьев (рис. 5.9, б). Последняя входит с ударом в контакт не в начале, а в середине рабочего участка линии зацепления при выходе с запаздыванием из соприкосновения предыдущей пары зубьев. В этом случае:
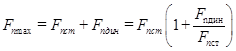 .
.
Разделив уравнение на bw (ширина зуба) и учитывая, что  , получим
, получим
 .
.
Обозначим  - коэффициент динамичности нагрузки, тогда
- коэффициент динамичности нагрузки, тогда
qрасч=qn kb kv.
В приближенных расчетах kv определяют из таблиц и графиков
kv=f (Vокр; ст.точн.).
Мероприятия по снижению динамических нагрузок:
1) повышение точности изготовления с ростом Vокр;
2) фланкирование зуба (рис. 5.10).
Последнее приводит к опусканию точки приложения силы к основанию зуба, где он прочнее. Для этого применяют специальную инструментальную рейку.

Лекция №6
Расчет зубчатого зацепления на контактную прочность
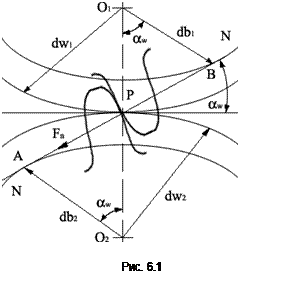
Расчет сводится к удовлетворению условия, по которому контактные напряжения зубьев не должны превышать допускаемые. Расчет ведут для зацепления в полюсе (рис. 6.1), т.к. выкрашивание начинается у полюсной линии.
В качестве исходной принимают формулу Герца-Беляева для наибольших контактных напряжений при скольжении цилиндров, соприкасающихся вдоль образующей
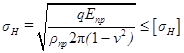 . (6.1)
. (6.1)
Входящие в формулу (6.1) величины известны из предыдущих лекций.
Обозначим 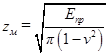 - коэффициент, учитывающий механические свойства материала колес. Для стальных колес zм=275 МПа.
- коэффициент, учитывающий механические свойства материала колес. Для стальных колес zм=275 МПа.
Получим 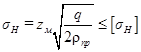 . (6.2)
. (6.2)
Здесь 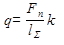 - погонная нагрузка, где
- погонная нагрузка, где 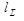 - длина контактных линий
- длина контактных линий
(в прямозубых передачах  );
); 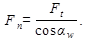
Так как  получаем
получаем 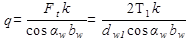 . (6.3)
. (6.3)
Приведенный радиус кривизны  . По свойству эвольвенты
. По свойству эвольвенты
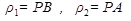 , поэтому
, поэтому 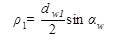 и
и 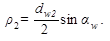
Так как  , следовательно
, следовательно
 и
и 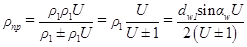 . (6.4)
. (6.4)
Подставив выражения (6.3) и (6.4) в уравнение (6.2), получим
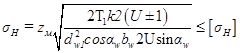 .
.
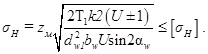 |
Так как
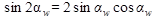 , то
, то Обозначим  - коэффициент, учитывающий форму сопряженных поверхностей ( при
- коэффициент, учитывающий форму сопряженных поверхностей ( при 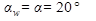 коэффициент
коэффициент 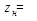
 ), тогда
), тогда
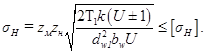 |
В передачах высокой точности (выше седьмой) вводится коэффициент

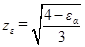 , учитывающий влияние коэффициента торцевого перекрытия
, учитывающий влияние коэффициента торцевого перекрытия 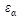 . Этот коэффициент получен экспериментальным путем. При отсутствии необходимости повышенной точности расчета можно принимать
. Этот коэффициент получен экспериментальным путем. При отсутствии необходимости повышенной точности расчета можно принимать 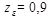 , что соответствует
, что соответствует  .
. Окончательно получим
 |
Таким образом, контактная прочность зубчатых колес определяется межосевым расстоянием, передаточным числом и шириной зубчатого венца, но не зависит от модуля.
