Последовательность расчета соединения с натягом

1. Определяют среднее контактное давление q_m по одной из формул (2.1, 2.2, 2.3) в зависимости от внешнего воздействия на соединение.

2. Определяют расчетный натяг по формуле (2.4).

3. Определяют поправку на обмятие микронеровностей по формуле (2.6).

4. Определяют (если это необходимо) поправку на температурную деформацию по формуле (2.7).

5. Определяют минимальный требуемый натяг соединения [N]_min по формуле (2.8).

6. Определяют максимальный расчетный натяг по условию возникновения пластических деформаций по формуле (2.13).

7. Определяют максимальный требуемый натяг по формуле (2.14).

8. Для полученных значений [N]_min и [N]_max подбирают посадку. По формулам (2.15...2.19) для выбранной посадки находят наименьший N_min и наибольший N_max вероятные натяги. Проверяют условия

N_min > [N]_min,

N_max£[N]_max.

9. Определяют усилие запрессовки при сборке соединения прессованием или температуру нагрева детали отверстия или температуру охлаждения детали вала при температурной сборке по формулам (2.20...2.22).

Пример расчета соединения с натягом

Подобрать посадку зубчатого колеса из стали 45 на вал из стали 40x, чтобы соединение было способно передавать крутящий момент Т=600 Нм. Размеры соединения: d= 60 мм; l =100 мм; d₂ = 120 мм. Шероховатость посадочных поверхностей вала и отверстия соответствует 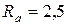мкм. Соединения собирают на прессе. В качестве смазочного материала используют трансформаторное масло. Коэффициент трения 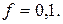Вал сплошной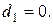

1. Определим контактное давление в соединении по формуле 2.2, приняв коэффициент запаса от сдвига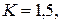

.

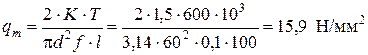2. Определим по табл. 1.2 модуль упругости и коэффициент Пуассона для сталей: 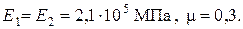Предел текучести для материала колеса (сталь 45)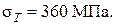

3. Расчетный минимальный натяг вычислим по формуле 2.4

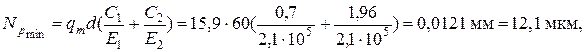
где

,

.

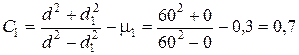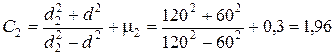4. Минимальный требуемый натяг определяем по формуле 2.8.

.

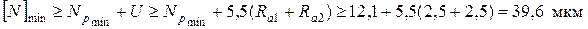5. Наибольший расчетный натяг (по формуле 2.13)

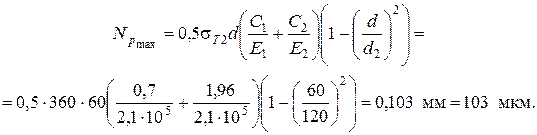
6. Максимальный требуемый натяг с учетом сглаживания микро неровностей вычислим по формуле 2.14:

.

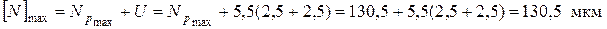7. По табл.2.2. и 2.3. подбираем посадку так, чтобы

.

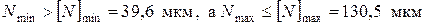В соответствии с этими условиями подходит посадка 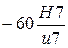; предельные отклонения отверстия для квалитета 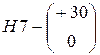; предельные отклонения вала для квалитета .

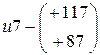Минимальный и максимальный натяги посадки:

.

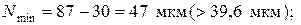
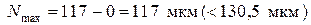Таким образом, для выполнения соединения следует назначить посадку .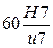

8. Определим для выбранной посадки 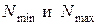с учетом рассеивания размеров отверстия и вала

а) допуски размеров:

отверстия Т_D=ES-EI=(30-0)=30 мкм,

вала Т_d=es-ei=(117-87)=30 мкм;

б) средние отклонения размеров:

отверстия E_m=0,5(ES+EI)=0,5(30-0)=15 мкм,

вала e_m=0,5(es+ei)=0,5(117+87)=102 мкм;

в) средний натяг посадки:

;

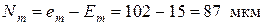г) рассеивание натяга:

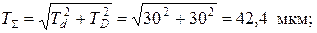
д) наибольший и наименьший вероятные натяги выбранной посадки:

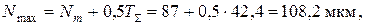
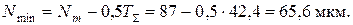
9. Наибольший расчетный вероятный натяг

.

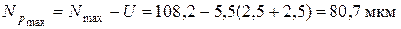10. Усилие запрессовки

.

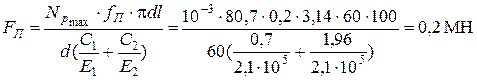3. Резьбовые соединения

Общие сведения

Резьбовыми соединениями называют разъемные соединения с помощью резьбовых крепежных деталей - винтов, болтов, шпилек, гаек или резьбы, нанесенной непосредственно на соединяемые детали. Основным элементом резьбового соединения является резьба, получаемая прорезанием на поверхности деталей канавок по винтовой линии.

Винтовую линию amn образует гипотенуза прямоугольного треугольника abc при его навивании на цилиндр (рис. 3.1).

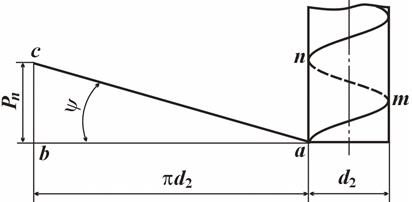
Рис. 3.1. Образование винтовой линии

Если плоскую фигуру, например, треугольник, трапецию и т. п., перемещать по винтовой линии так, чтобы ее плоскость при движении всегда проходила через ось винта, то эта фигура образует резьбу соответствующего профиля.

Резьбы классифицируют по следующим признакам:

- по форме поверхности, на которую наносится резьба, на цилиндрическую и коническую резьбу (наиболее распространена цилиндрическая резьба, коническую резьбу обычно применяют для плотных соединений труб, масленок, пробок и т. п.);

- по форме профиля - на треугольные, трапецеидальные, круглые и др.;

- по направлению винтовой линии - на правую и левую резьбу; болты с правой резьбой вывинчивают против часовой стрелки, а ввинчивают - по часовой (наиболее распространена правая резьба, левую резьбу применяют только в особых случаях, например в стяжках);

- по числу заходов ­– на одно-, двух- и многозаходные (если по параллельным винтовым линиям перемещают два или несколько рядом расположенных профилей, они образуют многозаходную резьбу);

- по назначению – на крепежные, крепежно-уплотнительные и ходовые.

Крепежная резьба обладает высокой прочностью и большим трением, предохраняющим соединяемые детали от самоотвинчивания; крепежно-уплотнительные, кроме указанных качеств обеспечивают повышенную плотность соединения; ходовые резьбы отличаются малым трением, чтобы иметь высокий КПД и уменьшить износ, а прочность во многих случаях не является здесь основным фактором. К крепежным резьбам относят метрические (рис. 3.2, а), и дюймовые с треугольным профилем; к крепежно-уплотнительным - трубную (рис. 3.2, б), имеющую треугольный профиль с закругленными вершинами и впадинами; к ходовым - трапецеидальную (рис. 3.2, в) и упорную (рис. 3.2, г).

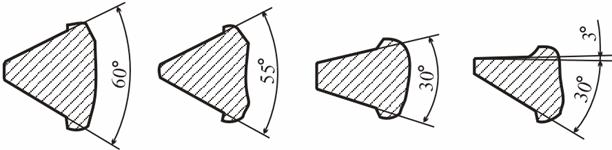
а б в г

Рис. 3.2. Крепежные резьбы

Резьба характеризуется следующими основными геометрическими параметрами, которые рассмотрим на примере метрической резьбы (рис. 3.3): d - наружный диаметр резьбы; d₁ - внутренний диаметр резьбы; d₂ - средний диаметр резьбы; р - шаг резьбы; Р_h - ход винта (для однозаходной резьбы Р_h = р; для многозаходной резьбы Р_h =n р, где n - число заходов), Н - высота теоретического профиля, h - рабочая высота профиля; a - угол профиля; y - угол подъема резьбы; kp - ширина основания профиля; k - коэффициент полноты резьбы (рис. 3.4),

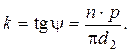
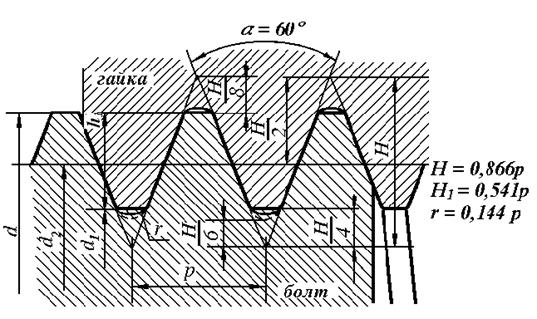
Рис. 3.3. Метрическая резьба

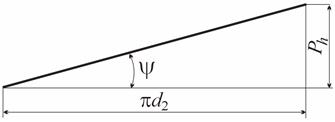
Рис. 3.4.

Геометрические параметры резьб и допуски на их размеры стандартизованы. Стандарт предусматривает метрические резьбы с крупным и мелким шагом.

При уменьшении шага соответственно уменьшаются глубина резьбы, что ведет к увеличению диаметра d₁ и повышению прочности, и угол подъема, что увеличивает самоторможение. По этим причинам мелкие резьбы находят применение для динамически нагруженных деталей, полых тонкостенных и мелких деталей (в авиации, точной механике и т. п.). В машиностроении основное применение имеют резьбы с крупным шагом, поскольку они менее чувствительны к ошибкам изготовления и износу.

Резьбу получают методом нарезания или накатывания. Для нарезания наружной резьбы используют различные резцы, плашки, резьбовые гребенки и фрезы, а для внутренней резьбы - метчики. Накатывают резьбу гребенками или роликами на резьбонакатных автоматах путем пластической деформации заготовки. Этим высокопроизводительным и дешевым методом изготовляют большинство резьб стандартных крепежных деталей. В литых и прессованных деталях резьба может быть получена при изготовлении деталей без механической обработки.

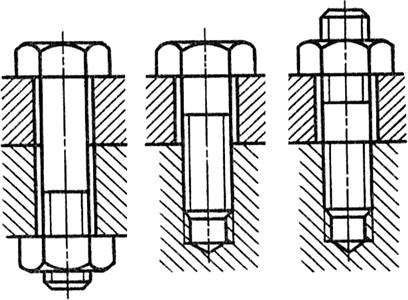
Для соединения деталей можно применять болты (рис. 3.5, а), винты (рис. 3.5, б) или шпильки (рис. 3.5, в). Болты имеют преимущественное применение, поскольку не требуют нарезания резьбы в соединяемых деталях. Это особо важно в тех случаях, когда материал детали не может обеспечить достаточную прочность и долговечность резьбы. Винты и шпильки применяют тогда, когда по конструкции соединения постановка болта не рациональна.

а б в

Рис. 3.5. Резьбовое соединение: а - болтом, б - винтом, в - шпилькой

Простую шайбу ставят под гайку или головку винта для уменьшения смятия детали гайкой, если деталь изготовлена из менее прочного материала (пластмассы, алюминия, дерева и т.п.); для предохранения чистых поверхностей деталей от царапин при завинчивании гайки (винта); для перекрытия зазора отверстия при большой его величине.

При затяжке резьбы зависимость между приложенным вращающим моментом Т и усилием затяжки F_а (рис. 3.6) имеет вид

,

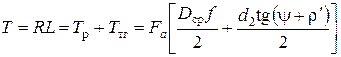где D_ср = (D₁ + d₀)/2»1,4 d - средний диаметр поверхности трения по торцу гайки; f - коэффициент трения по этой поверхности; L - длина ключа (плечо силы, прикладываемой к ключу); Т_р - момент трения в резьбе; Т_тг - момент трения по торцу гайки; r ^/ = arctg f ^/ - приведенный угол трения в резьбе; 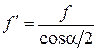- приведенный коэффициент трения в резьбе.

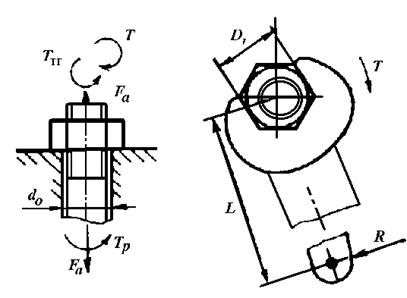
Рис. 3.6. Схема к анализу силовых факторов при затяжке резьбы (Т_{тг -} момент по торцу гайки, Т_р - момент в резьбе)

Окружная сила F_t в винтовой паре связана с усилием затяжки следующей зависимостью

F_t = F_a tg(y + r¢).

Условие y < r¢представляет собой условие самоторможения.

Для крепежных резьб угол подъема y = 1,5 – 4°, а угол трения r¢ изменяется в зависимости от величины коэффициента трения от 6 до 16°. Таким образом, все крепежные резьбы - самотормозящие. Ходовые резьбы выполняют как самотормозящими, так и несамотормозящими.

Хотя все крепежные резьбы удовлетворяют условию самоторможения, однако, как показывает практика, при переменной и ударной нагрузке наблюдается самоотвинчивание гаек и болтов. Существует много способов стопорения или предохранения от самоотвинчивания, которые основаны на следующих принципах:

1) стопорение дополнительным трением в резьбе путем постановки контргайки, самоконтрящейся гайки, пружинной шайбы и т.д. (рис. 3.7, а, б);

2) стопорение специальными элементами, которые жестко соединяют гайку со стержнем винта с помощью шплинта, проволоки и т.д. (рис. 3.7, в, г, д);

3) стопорение специальными элементами, которые жестко соединяют гайку с деталью с помощью стопорных шайб, планок или сваркой, (рис. 3.7 е, ж, з).

Основным критерием работоспособности резьбовых соединений является прочность. Под действием осевой силы в стержне винта возникают напряжения растяжения, в теле гайки - сжатия, в витках резьбы - смятия, среза, изгиба.

Около 90% разрушений резьбовых деталей носит усталостный характер. Чаще всего разрушение происходит по первому или второму витку, считая от опорного торца гайки; реже - в области сбега резьбы и в подголовочном сечении болта (винта).

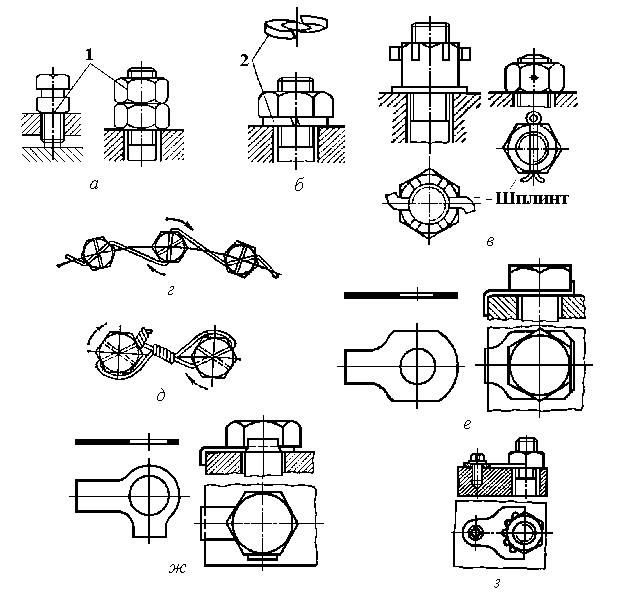
Рис. 3.7. Принципы и способы стопорения резьбовых соединений

Все стандартные болты, винты и шпильки изготовляют равнопрочными на разрыв стержня по резьбе, на срез резьбы и отрыв головки, поэтому расчет на прочность резьбового соединения обычно производят только по одному основному критерию работоспособности - прочности стержня. Расчетом определяют диаметр болта. Длину болта, винта или шпильки выбирают в зависимости от толщины соединяемых деталей. Остальные размеры деталей резьбового соединения (гайки, шайбы и др.) принимают исходя из диаметра резьбы по ГОСТу.

Расчет одиночных винтов

Расчет винтов (болтов, шпилек) зависит от условий их нагружения и технологических особенностей сборки соединения.

По условиям нагружения все винты подразделяются на воспринимающие осевую, поперечную или комбинированную нагрузку, неизменную или циклически изменяющуюся во времени. Существенные поправки в расчет могут внести дополнительные температурные нагрузки и внецентренное нагружение винтов.

В зависимости от технологических условий сборки винты могут быть ненапряженными (не затянутыми в процессе сборки) или напряженными (затянутыми), получающими значительную осевую нагрузку уже в процессе сборки, до приложения внешней рабочей нагрузки. Кроме того, винты можно устанавливать в отверстие свободно, с зазором или плотно, без зазора.

Основным видом нагружения винтов, для которого они и предназначены является осевое растяжение.

Возможны следующие расчетные случаи:

а) болт установлен с зазором без предварительной затяжки, нагружен осевой силой;

б) болт установлен с зазором и не нагружен осевой силой, но имеет предварительную затяжку;

в) болт установлен с зазором, затянут и дополнительно нагружен внешней осевой силой;

г) болт установлен с зазором и нагружен поперечной силой;

д) болт установлен без зазора и нагружен поперечной силой.

3.2.1. Расчет незатянутого болта, нагруженного внешней растягивающей силой

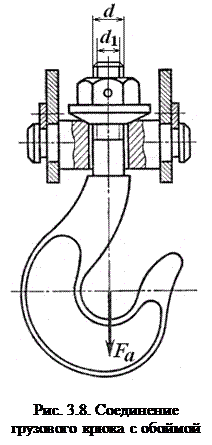
Примером такого соединения является соединение грузового крюка с обоймой (рис. 3.8). Стержень крюка работает только на растяжение. Резьбовое соединение, рассматриваемое в данном случае, называют ненапряженным.

Расчет сводится к определению внутреннего диаметра резьбы d₁из условия прочности на растяжение

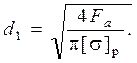
Далее по ГОСТ подбирается ближайший больший внутренний диаметр резьбы, соответствующий ему наружный диаметр d и все другие параметры резьбы.

3.2.2. Расчет затянутого болта, ненагруженного внешней осевой силой

Болт испытывает растяжение и кручение только от затяжки. В машиностроении такие болтовые соединения встречаются в клеммовых соединениях, в креплениях люков, крышек, в винтовых стяжках (рис. 3.9).

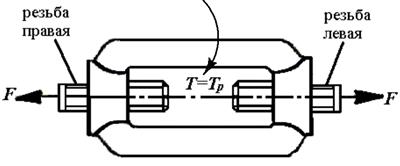
Рис. 3.9. Винтовая стяжка

В таких резьбовых соединениях стержень болта растягивается силой затяжки F_а и закручивается моментом Т_р в резьбе.

Эквивалентное напряжение в болте определяют по гипотезе энергии формоизменения (IV теория прочности):

s_экв =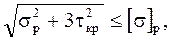

где s_p - напряжение растяжения в поперечном сечении болта;

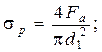
t_кр - наибольшее напряжение кручения, возникающее в точках контура поперечного сечения болта;

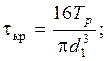
T_p - крутящий момент в резьбе;

T_p = 0,5d₂F_a tg(y + r ^/).

Принимая для стандартных стальных болтов с метрической резьбой

y = 2^о30^/, d₂/d₁= 1,12 и f = 0,15, чему соответствует r= 8^о40^/, получим

s_экв @ 1,3s_р £ [s]_p

или

s_экв =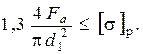

Откуда

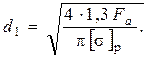
Следовательно, болт, работающий одновременно на растяжение и кручение, можно рассчитывать только на растяжение по расчетной силе, увеличенной по сравнению с силой, растягивающей болт в 1,3 раза. Рассмотренное выше соединение будем называть напряженным, а формулу для определения диаметра болта d₁ будем называть формулой напряженного болтового соединения.

3.2.3. Расчет затянутого и дополнительно нагруженного внешней осевой силой болта

Этот случай является весьма распространенным (фланцевые соединения труб и осесимметричных конструкций типа оболочек; крепление крышек резервуаров, находящихся под давлением; фундаментные болтовые соединения.

Для большинства резьбовых изделий требуется предварительная затяжка болтов, обеспечивающая плотность соединения и отсутствие взаимных смещений деталей стыка.

Рассмотрим резьбовое соединение для крепления крышки резервуара, находящегося под давлением (рис. 3.10).

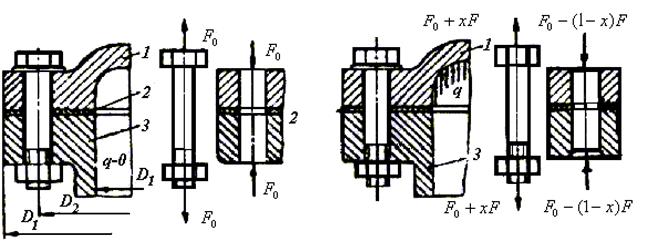
Рис. 3.10. Резьбовое соединение с затянутым болтом: 1 - крышка, 2 - прокладка, 3 - цилиндрический корпус

После затяжки болтов соединяемые детали (детали стыка) находятся под действием сжимающей силы F₀ (на участке действия одного болта), а болт растянут такой же силой F₀. При подаче жидкости или газа в резервуар внутреннее давление увеличивается и на соединяемые детали действует дополнительная нагрузка Q, которая пытается разъединить детали (раскрыть стык):

Q = pD₁² q/4,

где D₁ - внутренний диаметр соединяемых деталей; q - давление жидкости или газа внутри резервуара.

Таким образом, на участке действия одного болта помимо силы F₀, возникает сила F, по направлению совпадающая с F₀,

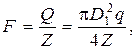
где Z - число болтов в соединении.

При нормальной работе соединения должно выполняться условие нераскрытия стыка (сила, сжимающая детали в стыке, должна быть всегда больше нуля). В этом случае часть нагрузки от внутреннего давления равная cF, дополнительно нагружает болт, а остальная часть, равная (1-c)F, идет на разгрузку стыка; здесь c- коэффициент внешней нагрузки, который соответствует приходящейся на болт доле внешней нагрузки F. В соответствии с условием нераскрытия стыка (сохранения плотности стыка) можно выразить усилие затяжки через внешнюю нагрузку

F₀ = k (1-c) F,

где k - коэффициент затяжки или коэффициент запаса по затяжке (k = 1,25...2,00 - при статической внешней нагрузке, k = 2...4 - при динамической - переменной - внешней нагрузке); c = 0,2...0,3 при жестких фланцах, c = 0,5...0,7 (иногда до 0,9) при податливых фланцах.

Осевая растягивающая сила, действующая на затянутый болт после приложения внешней нагрузки,

F_a = F₀ + cF = [k(1-c) + c]F.

Расчетную растягивающую нагрузку F_ар можно определить с учетом крутящего момента при затяжке

F_ap = 1,3F₀ + cF = [1,3k(1 - c) + c] F.

По F_ар можно определить необходимый внутренний диаметр болта по формуле ненапряженного болтового соединения.

3.2.4. Болтовое соединение нагружено силами, сдвигающими детали в стыке (поперечными по отношению к оси болта силами)

Условием надежности является отсутствие сдвига деталей. Соединение можно конструктивно выполнить двумя способами. Один способ - установка болта без зазора (рис. 3.11).

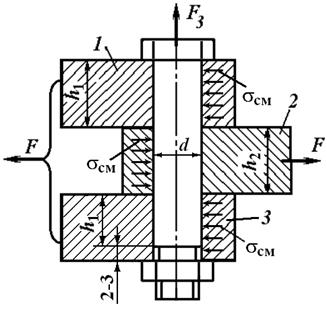
Рис. 3.11. Схема установки болта в отверстие без зазора

При этом обеспечивают напряженную посадку болта в отверстие. Силы трения в стыке не учитывают, поэтому затяжка болта необязательна. Длина части болта без резьбы должна быть меньше суммы толщин соединяемых деталей на 2-3 мм. Стержень болта рассчитывают по напряжениям среза и смятия. Условие прочности по напряжениям среза имеет вид

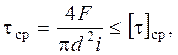
где i - число плоскостей среза (стыка);

i=Z-1,

где Z - число соединяемых деталей.

Следует обратить внимание, что в это уравнение входит диаметр d стержня болта, который может быть равен наружному диаметру резьбы или быть больше его.

Допускаемые напряжения на срез определяют из соотношений:

[t]_cp = 0,4 s_T - при действии статических нагрузок;

[t]_cp = (0,2...0,3)s_T - при действии переменных нагрузок.

Расчет на смятие выполняют по условным напряжениям. Условно принимают напряжения смятия равномерно распределенными по диаметральному сечению рассматриваемого участка стержня. Тогда условие прочности по напряжениям смятия можно записать в виде (соответственно для средней и крайних деталей):

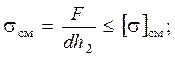
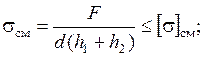
где h₁, h₂ - толщины соединяемых деталей.

Допускаемые напряжения на смятие [s]_см=0,8s_T - для стали и [s]_см=(0,4...0,5)s_T - для чугуна.

Другой способ - установка болта с зазором. В этом случае внешняя нагрузка уравновешивается силами трения, возникающими в плоскости стыка деталей 1, 2, 3 (рис. 3.12) вследствие прижатия деталей одна к другой под действием усилия затяжки болта.

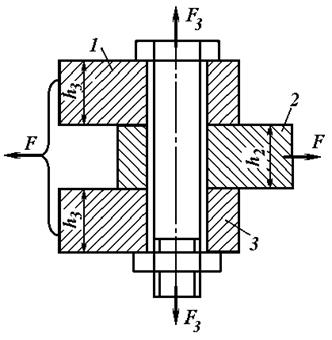
Рис. 3.12. Вариант установки болта с зазором

Условие отсутствия сдвига деталей в стыке

F £ i F_тр£ i F_a f .

Откуда

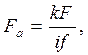
где F_тр- сила трения; f - коэффициент трения (f = 0,15...0,20 для сухих чугунных и стальных поверхностей); k - коэффициент запаса от сдвига (k = 1,3...1,5 при статической нагрузке, k = 1,8...2,0 при переменной нагрузке).

Прочность болта оценивают по формуле

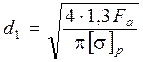
3.2.5. Болт находится под действием эксцентрично приложенной нагрузки

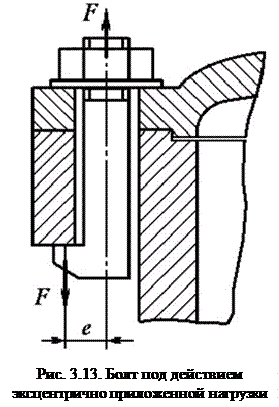Эксцентричная (смещенная относительно оси) нагрузка возникает в болтах с эксцентричной (костыльной) головкой или в нормальных болтах при непараллельности (перекосе) опорных поверхностей под гайкой и головкой болта. В таких болтах (рис. 3.11) под действием силы F после затяжки болта возникают напряжения растяжения

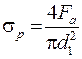
и изгиба

s_u =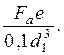

здесь F_a - осевая нагрузка; d₁ - внутренний диаметр резьбы; е - эксцентриситет приложения нагрузки (на практике d₁³ e ³0,6 d₁).

Болты с эксцентричной нагрузкой рассчитывают по эквивалентному напряжению

s_экв =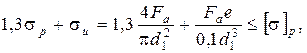

где 1,3 - коэффициент, учитывающий напряжения кручения при затяжке болта.

Обычно для упрощения расчета условно принимают e = d₁, тогда

s_экв = 11,6 F_a/d₁² £ [s]_p ,

отсюда можно определить внутренний диаметр болта.