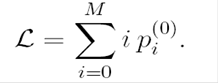Лекция 4. Стохастические модели
Одной из важнейших характеристик перекрестка является длина очереди автомобилей, ожидающих проезда. Построим простую модель образования очереди на перекрестке со светофорным регулированием. Рассмотрим пересечение двух дорог с односторонним движением. Пусть т+ - длительность горения зеленого света, а т - длительность всего цикла светофора. Предположим, что когда для одной полосы загорелся красный свет, зеленый свет для второй полосы загорается спустя некоторое время, чтобы „проскочившие“ автомобили успели проехать.
Пусть поток автомобилей, проходящих через точку А (некоторую точку на участке дороги перед перекрестком), есть простейший поток с параметром Л, Л > 0. При накоплении автомобилей в системе точка А сдвигается влево (рис.3).
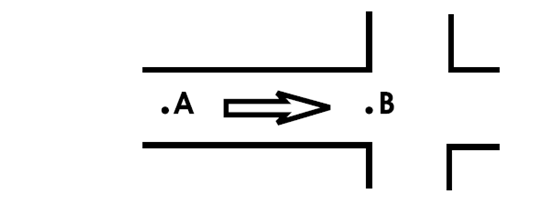
Рис. 3: Модель очереди на перекрестке.
Автомобили, поступающие в систему, либо пересекают перекресток (получают обслуживание как запросы), если проезд свободен и горит зеленый свет, либо становятся в очередь у перекрестка. Предположим, что водители не едут на красный свет, даже если на пересекающей полосе пусто.
Обслуживание одного автомобиля в рамках данной модели представляет собой проезд через точку В начало перекрестка. Примем время проезда через точку В одинаковым для всех автомобилей и равным T, Т > 0. За это время следующий автомобиль подъезжает к перекрестку (точке В) и ждет своего облуживания. Таким образом, поведение перекрестка будет описывается с помощью однолинейной системы массового обслуживания (СМО) с ожиданием и буфером размера M (максимальное число автомобилей, способных поместиться на дороге), MgN.
Будем искать среднюю длину очереди. Допустим, что перед перекрестком может стоять не более M автомобилей, M > 1. Каждый автомобиль занимает одну ячейку (одинаковой длины для всех автомобилей). Когда первый автомобиль проезжает через перекресток, остальные, стоящие в очереди, подвигаются на одну ячейку вперед.
Подсчитаем, сколько автомобилей могут проехать перекресток за период горения зеленого света. За единицу времени через перекресток могут проехать T-1 автомобилей. Значит, на зеленый свет через перекресток могут проехать τ+T-1автомобилей. Таким образом, величина 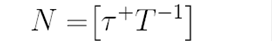 представляет собой пропускную способность перекрестка за время горения зеленого света, где [•] есть целая часть числа. Рассмотрим накопление автомобилей в системе за время одного цикла светофора. Будем исследовать поведение системы в моменты времени nT, n = 0, N, то есть моменты начала периода зеленого света и моменты окончания обслуживания запросов (автомобилей). Обозначим через p вероятности того, что в момент времени nT + 0 (непосредственно сразу после ухода автомобиля из очереди) длина очереди составляет i автомобилей, n = 0, N, i = 0, M. Обозначим также через Pt(t) вероятность того, что за время t в систему приедут i автомобилей, i > 0. Выражение для Pt(t) имеет вид
представляет собой пропускную способность перекрестка за время горения зеленого света, где [•] есть целая часть числа. Рассмотрим накопление автомобилей в системе за время одного цикла светофора. Будем исследовать поведение системы в моменты времени nT, n = 0, N, то есть моменты начала периода зеленого света и моменты окончания обслуживания запросов (автомобилей). Обозначим через p вероятности того, что в момент времени nT + 0 (непосредственно сразу после ухода автомобиля из очереди) длина очереди составляет i автомобилей, n = 0, N, i = 0, M. Обозначим также через Pt(t) вероятность того, что за время t в систему приедут i автомобилей, i > 0. Выражение для Pt(t) имеет вид
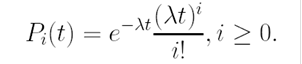
Уравнения для вероятностей p(in),n = 0, N, i > 0 имеют вид
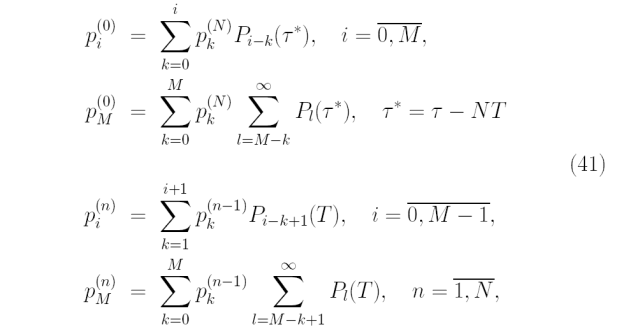
причем каждая группа вероятностей pi(n), i = 0,M удовлетворяет условиям нормировки
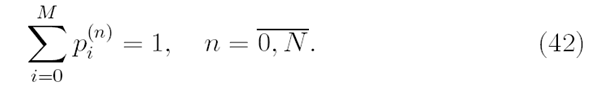 Обозначим через
Обозначим через 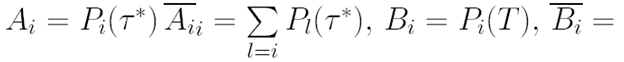
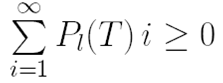 и распишем систему (41) более подробно:
и распишем систему (41) более подробно:
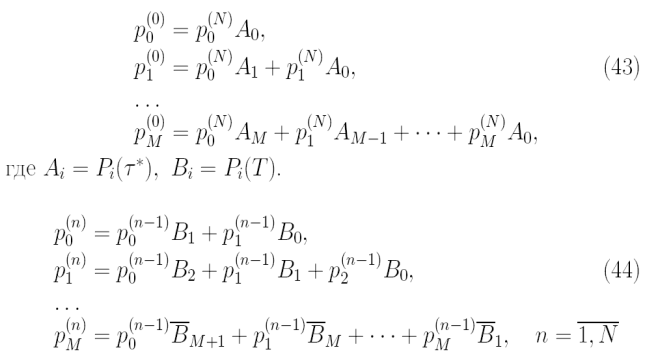
Запишем системы (43) и (44) в матричном виде
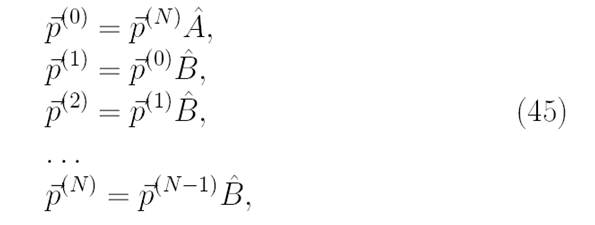
Где
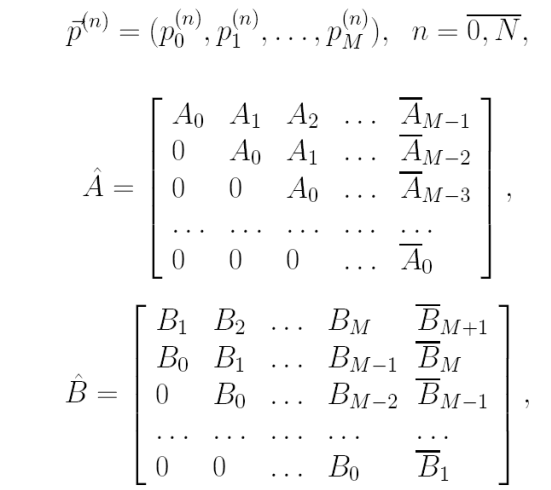
Из системы (45) и условия нормировки (42) при n = 0 находим значение для вектора
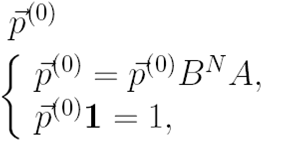
где 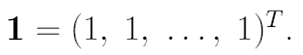
Остальные векторы вероятностей находим с помощью равенств
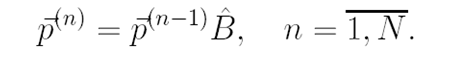
Тогда средняя длина очереди на перекрестке к моменту начала периода зеленого света равна