Расчет статически неопределимых ферм

Практически все фермы из-за наличия жесткости в узловых соединениях являются статически неопределимыми конструкциями. Возможность пренебрежения жесткостью узлов при расчете ферм практически допустима. Нами рассматриваемые фермы являются шарнирно-стержневыми системами. Применяемые в ТТ фермы могут быть как внутренне, так и внешне статически неопределимыми, а также одновременно статически неопределимыми- и внешне, и внутренне. На рис.53,а показана опора верхнего строения крана, которая из-за затяжки между нижними опорами является один раз внутренне статически неопределимой. За основную систему следует принять конструкцию без затяжки с единичной силой X₁ в направлении затяжки. 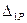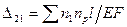Тогда каноническое уравнение будет иметь вид (δ₃₁l₃+δ₁₁) X₁+ =0, где δ₁₁ и определяются по зависимости , а удлинение затяжки от силы х₁ = 1 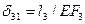, где l₃ и F₃ – длина и площадь поперечного сечения затяжки. Отсюда неизвестное усилие

(97)

где N_i1 и N_ip – усилия в стержнях фермы (основной системы) от силы х₁ и от нагрузки (на рис.53 не показана), которые могут быть определены, например, с помощью построений диаграмма Максвелла – Кремоны. Для определения значения х₁ по формуле (97) длины стержней в известны и необходимо задаться сечениями всех стержней фермы. Для первоначального определение сечений стержней можно статически неопределимую систему заменить статической определимой (пренебречь влиянием затяжки).

При этом найденные усилия в стержнях будут несколько преувеличены и после нахождения значения х₁ по формуле (97) может потребоваться пересчет. Если затяжка можного сечения, что иногда место, то её продольной деформацией можно пренебречь и тогда фермы надлежит рассматривать как внешне статически один раз неопределимую систему, а

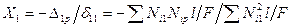(98)

Существуют также искусственные приемы создания статически определимых систем для предварительного определения сечений стержней. Так, во внешне статически неопределимой системе (рис.53, б), если отбросить 1, то ферма делается статической определимой (трехшарнирная арка с верхним шарниром 0). Практика расчетов таких крановых опор показывает, что обычно при таком приеме пересчет сечений не требуется. Окончательно усилие в любом стержне определяется по формуле

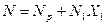(99)

Вычисления удобно располагать в следующей табличной форме:

Номер стержня	L/F	N1	NP		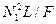	N
:	:	:	:	:	:	:

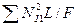При расчете фермы на заданное температурное воздействие каноническое уравнение будет иметь вид

, (100)

где 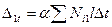. Здесь 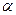– коэффициент линейного расширения; 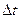- изменение температуры стержня по сравнению с начальной; N_i1 – усилие, вызванное единичной силой X₁.

Тогда

Так как . Усилие в любом стержне выразится формулой N=N₁X₁.

Расчет балочных конструкций на действие подвижной нагрузки основывается на построении линий влияния для опорных реакций R₁ изгибающих моментов М, перерезывающих сил Q . Для построения линий влияния в статически неопределимой конструкции надо, выбрав для нее основную систему решить статически неопределимую задачу от действия единичной силы Р, находящейся на произвольном расстоянии Х от опоры на данном пролете. Покажем построение линий влияния на некоторых примерах.

Пусть дана один раз статически неопределимая балка (рис.54, а). Основная система приведена на рис.54, б. Из канонического уравнения 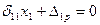находим .

Пользуясь правилом Верещагина, определяем (рис.54, в, г) и δ₁₁ (рис.54, г). Тогда 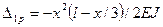, , 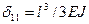. (101)

Таким образом, Х₁ представляет собой кубическую параболу. Линия влияния реакции опоры В приведена на рис. 54, д. Линия влияния перерезывающих сил Q и изгибающих моментов М строим, пользуясь принципом независимости действия сил, путем суммирования линий влияния от единичного груза Р и от неизвестной Х₁ в основной системе. При этом линия влияния (рис.54, з), где Q_p=1 (рис.54, е) и Q_x1=1 (рис.54, ж). Аналогично линия влияния (рис.54, л), где (рис.54, и) и (рис.54, к).

Пусть дана дважды статически неопределимая трехпролетная балка (рис.55, а). Основная система приведена на (рис.55, б). Для составления системы канонических уравнений пользуемся теоремой о трех моментах, применяя формулу (96). Пусть единичная сила Р находится на первом пролете (рис.55, в). Тогда, учитывая параметры эпюры изгибающих моментов, уравнения будут равны:

(102)

Рисунок 55 – Линии влияния опорных моментов у трехпролетной балки.

Решая систему уравнений (102), находим:

(103)

По формулам (103) строим линии влияния на первом пролете на рис.55,д,е. Однако если вести расчет с другого конца балки, то будет получаться такой же результат, только обозначения М₁ и М₂ поменяются местами. С учетом этого по формулам (103) можно построит линии влияния и для третьего пролета. Для построения линии влияния во втором пролете надо приложить туда единичную силу Р и построить от нее эпюру изгибающих моментов (рис.55, г).

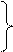Теперь вместо уравнений (102) будем иметь:

(104)

Решая эту систему, находим:

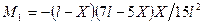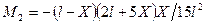и (105)