Как интерпретировать значение относительного риска?
Показатель относительного риска сравнивается с 1 для того, чтобы определить характер связи фактора и исхода:
- Если ОР равен 1, можно сделать вывод, что исследуемый фактор не влияет на вероятность исхода (отсутствие связи между фактором и исходом).
- При значениях более 1 делается вывод о том, что фактор повышает частоту исходов (прямая связь) – фактор агрессии
- При значениях менее 1 - о снижении вероятности исхода при воздействии фактора (обратная связь) – фактор защиты
Также обязательно оцениваются значения границ 95% доверительного интервала. Если оба значения - и нижней, и верхней границы - находятся по одну сторону от 1, или, другими словами, доверительный интервал не включает 1, то делается вывод о статистической значимости выявленной связи между фактором и исходом с вероятностью ошибки p<0,05.
Если нижняя граница 95% ДИ меньше 1, а верхняя - больше, то делается вывод об отсутствии статистической значимости влияния фактора на частоту исхода, независимо от величины показателя ОР (p>0,05).
ЗАДАЧА-ЭТАЛОН
В 1999 году в Оклахоме проводились исследования заболеваемости мужчин язвой желудка. В качестве влияющего фактора было выбрано регулярное потребление фастфуда. В первой группе находились 500 мужчин, постоянно питающихся быстрой пищей, среди которых язву желудка диагностировали у 96 человек. Во вторую группу были отобраны 500 сторонников здорового питания, среди которых язва желудка была диагностирована в 31 случае. Исходя из полученных данных была построена следующая таблица сопряженности:
| Больные язвой желудка (1) | Язва желудка отсутствует (0) | Всего | |
| Фастфуд (1) | |||
| Здоровое питание (0) | |||
| Всего |
1. Рассчитываем значение относительного риска:
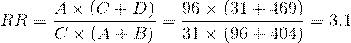
2. Находим значения верхней и нижней границ 95% доверительного интервала по указанным выше формулам. Значение верхней границы составляет 4.55, нижней - 2.11.
3. Сравниваем полученные значения ОР и 95% ДИ с 1. Показатель относительного риска свидетельствует о наличии прямой связи между употреблением фастфуда и вероятностью развития язвы желудка. У мужчин, употребляющих картошку фри и хотдоги, язва желудка наблюдается в 3,1 раза чаще, чем среди придерживающихся здорового питания. Уровень значимости данной взаимосвязи соответствует p<0.05, так как 95% ДИ не включает в себя единицу.
Тема 11. Критерий χ2 Пирсона.
Критерий χ2Пирсона – это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).
1. История разработки критерия χ2
Критерий хи-квадрат для анализа таблиц сопряженности был разработан и предложен в 1900 году английским математиком, статистиком, биологом и философом, основателем математической статистики и одним из основоположников биометрики Карлом Пирсоном(1857-1936).
2. Для чего используется критерий χ2 Пирсона?
Критерий хи-квадрат может применяться при анализе таблиц сопряженности, содержащих сведения о частоте исходов в зависимости от наличия фактора риска. Например, четырехпольная таблица сопряженностивыглядит следующим образом:
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | A | B | A + B |
| Фактор риска отсутствует (0) | C | D | C + D |
| Всего | A + C | B + D | A + B + C + D |
Таблица 4. Четырехпольная таблица (таблица2х2)
Как заполнить такую таблицу сопряженности? Рассмотрим небольшой пример.
Проводится исследование влияния курения на риск развития артериальной гипертонии. Для этого были отобраны две группы исследуемых - в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую - 80 некурящих такого же возраста. В первой группе у 40 человек отмечалось повышенное артериальное давление. Во второй - артериальная гипертония наблюдалась у 32 человек. Соответственно, нормальное артериальное давление в группе курильщиков было у 30 человек (70 - 40 = 30) а в группе некурящих - у 48 (80 - 32 = 48).
Заполняем исходными данными четырехпольную таблицу сопряженности:
| Артериальная гипертония есть (1) | Артериальной гипертонии нет (0) | Всего | |
| Курящие (1) | |||
| Некурящие (0) | |||
| Всего |
В полученной таблице сопряженности каждая строчка соответствует определенной группе исследуемых. Столбцы - показывают число лиц с артериальной гипертонией или с нормальным артериальным давлением.
Задача, которая ставится перед исследователем: имеются ли статистически значимые различия между частотой лиц с артериальным давлением среди курящих и некурящих? Ответить на этот вопрос можно, рассчитав критерий хи-квадрат Пирсона и сравнив получившееся значение с критическим.
