Измерение (определение) расстояний и площадей по карте
Численный масштаб– масштаб карты, выраженный дробью, числитель которой – единица, а знаменатель – число, показывающее степень уменьшения на карте линий местности; чем меньше знаменатель масштаба, тем крупнее масштаб карты. Подпись численного масштаба на картах обычно сопровождается указанием величины масштаба – расстояния на местности (в метрах или километрах), соответствующего одному сантиметру карты. Величина масштаба в метрах соответствует знаменателю численного масштаба без двух последних нулей. При определении расстояния с помощью численного масштаба линия на карте измеряется линейкой, полученный результат в сантиметрах умножается на величину масштаба.
Линейный масштаб– графическое выражение численного масштаба. Он представляет собой прямую линию, разделенную на определенные части, которые сопровождаются подписями, означающими расстояния на местности. Линейный масштаб служит для измерения и откладывания расстояний на карте. На рис. 6.10 расстояние между точками А и В равно 1850 м.
Рис. 6.10.Измерение расстояний по линейному масштабу Поперечный масштаб– график (обычно на металлической пластинке) для измерения и откладывания расстояний на карте с предельной графической точностью (0,1 мм).
Стандартный (нормальный) поперечный масштаб имеет большие деления, равные 2 см, и малые деления (слева на графике), равные 2 мм. Кроме того, на графике имеются отрезки между вертикальной и наклонной линиями, равные по первой горизонтальной линии 0,2 мм, по второй – 0,4 мм, по третьей – 0,6 мм и т. д. С помощью стандартного поперечного масштаба можно измерять и откладывать расстояния на карте любого (метрического) масштаба. Отсчет расстояния по поперечному масштабу состоит из суммы отсчета на основании графика и отсчета отрезка между вертикальной и наклонной линиями. На рис. 6.11 расстояние между точками А и В (при масштабе карты 1:100 000) равно 5500 м (4 км + 1400 м + 100 м).
Рис. 6.11.Измерение расстояний по поперечному масштабу Измерение расстояний циркулем–измерителем.При измерении расстояния по прямой линии иглы циркуля устанавливают на конечные точки, затем, не изменяя раствора циркуля, по линейному или поперечному масштабу отсчитывают расстояние. В том случае, когда раствор циркуля превышает длину линейного или поперечного масштаба, целое число километров определяется по квадратам координатной сетки, а остаток – обычным порядком по масштабу. Ломаные линии удобно измерять путем последовательного наращивания раствора циркуля прямолинейными отрезками (рис. 6.12).
Измерение длин кривых линий производится последовательным отложением шага циркуля (рис. 6.13). Величина шага циркуля зависит от степени извилистости линии, но, как правило, не должна превышать 1 см. Для исключения систематической ошибки длину шага циркуля, определенную по масштабу или линейке, следует проверять измерением линии километровой сетки длиной 6–8 см.
Рис. 6.12.Измерение расстояний способом наращивания раствора циркуля Длина извилистой линии, измеренной по карте, всегда несколько меньше ее действительной длины, так как измеряются не кривая линия, а хорды отдельных участков этой кривой; поэтому в результаты измерений по карте приходится вводить поправку – коэффициенты увеличения расстояний. Рис.
Рис. 6.13.Измерение расстояний шагом циркуля
Измерение расстояний курвиметром.Вращением колесика стрелку курвиметра устанавливают на нулевое деление, а затем прокатывают колесико по измеряемой линии с равномерным нажимом слева направо (или снизу вверх); полученный отсчет в сантиметрах умножают на величину масштаба данной карты. Определение расстояний по прямоугольным координатамв пределах одной зоны можно произвести по формуле
где D – длина линии; x1, y1 – координаты начальной точки прямой; x2, y2 – координаты конечной точки прямой. Определение площадей по квадратам километровой сетки.Площадь участка определяется подсчетом целых квадратов и их долей, оцениваемых на глаз. Каждому квадрату километровой сетки соответствует: на картах масштаба 1:25 000 и 1:50 000 – 1 км2, на картах масштаба 1:100 000 – 4 км2, на картах масштаба 1:200 000 – 16 км2. Прямоугольные координаты на картах Прямоугольные координаты(плоские) – линейные величины: абсцисса х и ордината у, определяющие положение точек на плоскости (на карте) относительно двух взаимно перпендикулярных осей X и Y (рис. 6.14). Абсцисса X и ордината Y точки А – расстояния от начала координат до оснований перпендикуляров, опущенных из точки А на соответствующие оси, с указанием знака. В топографии и геодезии, а также на топографических картах ориентирование производится по северу со счетом углов по ходу часовой стрелки, поэтому для сохранения знаков тригонометрических функций положение осей координат, принятое в математике, повернуто на 90°. Прямоугольные координаты на топографических картах РФ применяются по координатным зонам. Координатные зоны – части земной поверхности, ограниченные меридианами с долготой, кратной 6°. Первая зона ограничена меридианами 0° и 6°, вторая – 6° и 12°, третья—12° и 18° и т.д. Счет зон идет от Гринвичского меридиана с запада на восток. Протяженность каждой зоны с севера на юг – порядка 20 000 км. Ширина зоны на экваторе – около 670 км, на широте 40° – 510 км, на широте 50 °– 430 км, на широте 60° – 340 км.
Рис. 6.14.Прямоугольные координаты
Все топографические карты в пределах данной зоны имеют общую систему прямоугольных координат. Началом координат в каждой зоне служит точка пересечения среднего (осевого) меридиана зоны с экватором (рис. 6.15), средний меридиан зоны соответствует оси абсцисс, а экватор – оси ординат. При таком расположении координатных осей абсциссы точек, расположенных южнее экватора, и ординаты точек, расположенных западнее среднего меридиана, будут иметь отрицательные значения. Для удобства пользования координатами на топографических картах принят условный счет ординат, исключающий отрицательные значения ординат. Это достигнуто тем, что отсчет ординат идет не от нуля, а от величины 500 км, т. е. начало координат в каждой зоне как бы перенесено на 500 км влево вдоль оси Y. Кроме того, для однозначного определения положение точки по прямоугольным координатам на земном шаре к значению координаты Y слева приписывается номер зоны (однозначное или двузначное число). Зависимость между условными координатами и их действительными значениями выражается формулами X' = X; Y' = Y – 500 000, где X и Y – действительные значения координат; X, Y – условные значения координат. Например, если точка имеет координаты X =5 650 450; Y =3 120 840, то это значит, что точка расположена в третьей зоне на удалении 120 км 840 м от среднего меридиана зоны (620 840–500 000) и к северу от экватора на удалении 5650 км 450 м. 
Рис. 6.15.Система прямоугольных координат на топографических картах: а – одной зоны; б – части зоны Полные координаты– прямоугольные координаты, записанные (названные) полностью, без каких–либо сокращений. В примере, приведенном выше, даны полные координаты объекта: X = 5 650 450; Y = 3 620 840. Сокращенные координатыприменяются для ускорения целеуказания по топографической карте, в этом случае указываются только десятки и единицы километров и метры. Например, сокращенные координаты данного объекта будут: X = 50 450; Y = 20 840. Сокращенные координаты нельзя применять при целеуказании на стыке координатных зон и если район действий охватывает пространство протяженностью более 100 км по широте или долготе. Координатная (километровая) сетка– сетка квадратов на топографических картах, образованная горизонтальными и вертикальными линиями, проведенными параллельно осям прямоугольных координат через определенные интервалы (табл. 6.4). Эти линии называются километровыми. Координатная сетка предназначается для определения координат объектов и нанесения на карту объектов по их координатам, для целеуказания, ориентирования карты, измерения дирекционных углов и для приближенного определения расстояний и площадей. Таблица 6.4Координатные сетки на картах
На карте масштаба 1:500 000 координатная сетка полностью не показывается – наносятся только выходы километровых линий по сторонам рамки (через 2 см). При необходимости по этим выходам координатная сетка может быть прочерчена на карте. Километровые линии на картах подписываются у их зарамочных выходов и у нескольких пересечений внутри листа (рис. 6.16). Крайние на листе карты километровые линии подписываются полностью, остальные – сокращенно, двумя цифрами (т. е. указываются только десятки и единицы километров). Подписи у горизонтальных линий соответствуют расстояниям от оси ординат (экватора) в километрах. Например, подпись 6082 в правом верхнем углу показывает, что данная линия отстоит от экватора на 6082 км. Подписи вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно перенесенного к западу от среднего меридиана на 500 км. Например, подпись 4308 в левом нижнем углу означает: 4 – номер зоны, 308 – расстояние от условного начала координат в километрах.
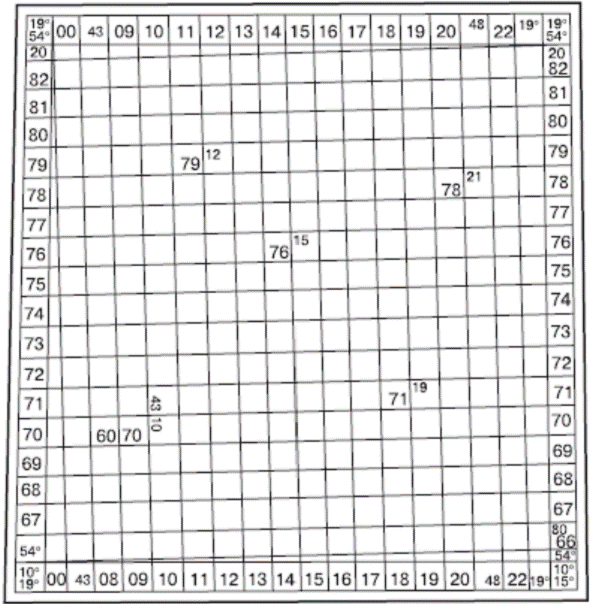
Рис. 6.16.Координатная (километровая) сетка на листе карты Дополнительная координатная (километровая) сетка может быть нанесена на топографических картах масштаба 1:25 000, 1:50 000, 1:100 000 и 1:200 000 по выходам километровых линий в смежной западной или восточной зоне. Выходы километровых линий в виде черточек с соответствующими подписями даются на картах, расположенных на протяжении 2° к востоку и западу от граничных меридианов зоны.
Дополнительная координатная сетка предназначается для преобразования координат одной зоны в систему координат другой, соседней, зоны. При необходимости дополнительная координатная сетка прочерчивается на листе карты путем соединения одноименных черточек на противоположных сторонах рамки. Вновь построенная сетка является продолжением километровой сетки листа карты смежной зоны и должна полностью совпадать (смыкаться) с ней при склейке карты. Определение прямоугольных координат по карте и нанесение объектов на карту по координатам Определение прямоугольных координат объекта по карте циркулемЦиркулем по перпендикуляру измеряют расстояние от данного объекта до нижней километровой линии и по масштабу определяют его действительную величину. Затем эту величину в метрах приписывают справа к подписи километровой линии, а при длине отрезка более километра вначале суммируют километры, а затем также приписывают число метров справа. Это будет координата объекта X (абсцисса). Таким же приемом определяют и координату Y (ординату), только расстояние от объекта измеряют до левой стороны квадрата. При отсутствии циркуля расстояния измеряют линейкой или полоской бумаги. Пример определения координат объекта А показан на рис. 6.17: X = 5 877 100; Y = 3 302 700. Здесь же дан пример определения координат объекта В, расположенного у рамки листа карты в неполном квадрате: X = 5 874 850; Y = 3 298 800. Определение прямоугольных координат координатомером
Координатомер – приспособление для отсчета координат. Наиболее распространен координатомер в виде прямого угла прозрачной линейки, по сторонам которого нанесены миллиметровые деления. Такого типа координатомер имеется на командирской линейке. При определении координат координатомер накладывают на квадрат, в котором располагается объект, совмещая вертикальную шкалу с его левой стороной, а горизонтальную – с объектом.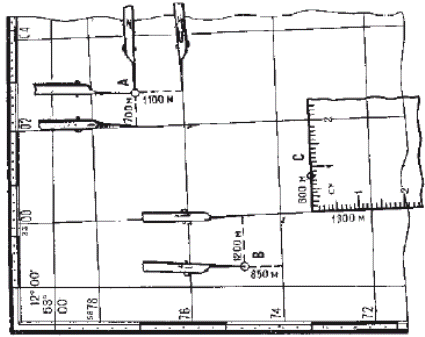 
Рис. 6.17.Определение прямоугольных координат объектов по карте Отсчеты в миллиметрах (десятые миллиметра отсчитывают на глаз) в соответствии с масштабом карты преобразуют в действительные величины – километры и метры, а затем величину, полученную по вертикальной шкале, суммируют (если она больше километра) с оцифровкой нижней стороны квадрата или приписывают к ней справа (если величина меньше километра). Это будет координата X объекта. Таким же порядком получают и координату Y – величину, соответствующую отсчету по горизонтальной шкале, только суммирование производят с оцифровкой левой стороны квадрата. Нанесение объекта на карту по прямоугольным координатам циркулем или линейкойПрежде всего по координатам объекта в километрах и оцифровкам километровых линий находят на карте квадрат, в котором должен быть расположен объект. Квадрат местонахождения объекта на карте масштаба 1:50 000, где километровые линии проведены через 1 км, находят непосредственно по координатам объекта в километрах.
Рис. 6.18.Нанесение объектов на карту по прямоугольным координатам
На карте масштаба 1:100 000 километровые линии проведены через 2 км и подписаны четными числами, поэтому, если одна или две координаты объекта в километрах – нечетные числа, нужно находить квадрат, стороны которого подписаны числами на единицу меньше соответствующей координаты в километрах. На карте масштаба 1:200 000 километровые линии проведены через 4 км, поэтому стороны нужного квадрата будут подписаны числами, кратными четырем, меньшими соответствующей координаты объекта в километрах на один, два или три километра. Например, если даны координаты объекта (в километрах) X = 6755 и Y = 4613, то стороны квадрата будут иметь оцифровки 6752 и 4612. После нахождения квадрата, в котором расположен объект, рассчитывают удаление объекта от нижней стороны квадрата и откладывают его в масштабе карты от нижних углов квадрата вверх. К полученным точкам прокладывают линейку и от левой стороны квадрата, также в масштабе карты, откладывают расстояние, равное удалению объекта от этой стороны. На рис. 6.18 показан пример нанесения на карту объекта А по координатам X = 3 768 850, Y = 29 457 500. Нанесение объекта на карту координатомером, выгравированным на командирской линейке
По координатам объекта в километрах и оцифровке километровых линий определяют квадрат, в котором находится объект. На этот квадрат накладывают координатомер так же, как и при определении координат (см. рис. 6.17), совмещают его вертикальную шкалу с западной стороной квадрата так, чтобы против нижней стороны квадрата был отсчет, соответствующий координате X в масштабе карты минус оцифровка этой стороны квадрата. Затем, не изменяя положения координатомера, находят на горизонтальной шкале отсчет, соответствующий (также в масштабе карты) разности координаты Y объекта и оцифровки западной стороны квадрата. Точка против штриха у этого отсчета будет соответствовать положению объекта на карте. На рис. 6.18 показан пример нанесения на карту объекта В, расположенного в неполном квадрате, по координатам X = 3 765 500; Y = = 2 945 750. В данном случае координатомер наложен так, чтобы горизонтальная шкала его была совмещена с северной стороной квадрата, а отсчет против западной его стороны соответствовал разности координаты Y объекта и оцифровки этой стороны (29 457 км 650 м – 29 456 км = = 1 км 650 м). Отсчет, соответствующий разности оцифровки северной стороны квадрата и координате Y объекта (3766 км – 3765 км 500 м), отложен по вертикальной шкале вниз. Точка против штриха у отсчета 500 м будет указывать положение объекта на карте.
Движение по азимутам - способ выдерживания направления пути (маршрута) с помощью компаса; он применяется при плохой видимости (ночью, в туман и т.п.) и на местности, бедной ориентирами (в лесу, в пустыне и т.п.), а также при отсутствии карт на незнакомой местности.
Движение по азимутам совершается от ориентира до ориентира. Предварительно (до начала движения) подготавливаются необходимые данные:
- на карте намечаются маршруты движения с ориентирами у поворотов;
- определяются магнитные азимуты и длина каждого участка (колена) маршрута.
Для определения магнитного азимута по карте измеряется дирекционный угол
направления и к нему прибавляется поправка на магнитное склонение,
указанная на нижнем обрезе карты;
- данные для движения вписываются в таблицу (табл.2), либо записываются
непосредственно на карте или специально составленной схеме
| Дирек- | Поправ- | Магнит- | Расстояние | ||
| Номер и наименование ориентира | цион-ные углы, градусы | ка на маг-нитное отклоне-ние, градусы | ные азимуты, градусы | в метрах | в парах шагов |
| 1 - отдельный двор 2 - место, где дорога входит в лес 3 - перекресток дороги и просеки 4 - яма у просеки 5 - дом лесника |
Магнитный азимут - горизонтальный угол, измеряемый по ходу часовой стрелки от северного направления магнитного меридиана до направления на предмет. Его значения могут быть от 00 до 3600.
Дирекционный угол - угол между проходящим через данную точку направлением и линией, параллельной оси абсцисс. Его значения могут быть от 00 до 3600.
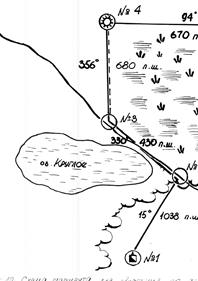
Рис.10 Схема маршрута для движения по азимуту.
1. Установи на шкале компаса против мушки отсчет, равный значению заданного магнитного азимута.
2. Отпустив тормоз магнитной стрелки, поверни компас в горизонтальной плоскости так, чтобы северный конец стрелки установился против нулевого деления шкалы.
3. не меняя положения компаса, заметь на местности по линии визирования через целик и мушку какой-нибудь удаленный ориентир. Направление на ориентир и будет направлением, соответствующим заданному азимуту.
4. Учись двигаться прямолинейно, особенно на закрытой местности. Так как шаг одной ноги человека меньше шага другой ноги, человек незаметно для себя отклоняется в сторону, если не следить за направлением движения.
5. В движении веди отсчет пройденного расстояния парами шагов или по времени.