Анализ качественных признаков на основе логлинейной модели
Весьма распространенной проблемой в медицинских исследованиях является анализ качественных номинальных признаков, которые, как правило, представляются в виде кодов (например, цвет кожных покровов: розоватый 1, желтый 2, пунцовый 3 и т.д.). Интерес представляет частота встречаемости признаков в различных группах, а также сила и направление влияния одних признаков на другие. Нами уже были рассмотрены таблицы сопряженности 2×2, которые используются для анализа совместного распределения двух признаков, имеющих по две градации. Задачу можно сформулировать другими словами – оценка взаимного влияния двух двухуровневых факторов. Однако, встречаются более сложные случаи – многомерные таблицы сопряженности, например, нужно выяснить зависит ли срок госпитализации от возраста пациента и тяжести его состояния при поступлении в стационар (в каждую ячейку вводится число случаев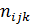 
).
Таблица 75. Влияние двухуровневых факторов
| сроки госпитализации | ||||
| тяжесть состояния при поступлении | возраст | до 5 дней | от 5 до 10 дней | > 10 дней |
| легкая степень | до 40 лет | n111 | n211 | … |
| 4060 лет | n112 | n212 | … | |
| > 60 лет | n113 | n213 | … | |
| средняя степень | до 40 лет | n121 | n221 | … |
| 4060 лет | n122 | n222 | … | |
| > 60 лет | n123 | n223 | … |
В данном примере фактор А «срок госпитализации» имеет три уровня (i=1,2,3), фактор В«возраст» два уровня (j=1,2), и фактор С –«тяжесть состояния» три уровня (k=1,2,3).
Один из способов решения подобных задач – построение логлинейной модели вида:
+ 
+ 
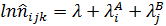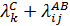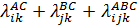, (78)
где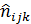 
теоретические частоты наблюдений
λ логарифмы эффектов различных сочетаний факторов А, В, и С на различных уровнях (интерпретируется как вклад факторов и их сочетаний в частоту).
Переходя от логарифмов к натуральным значениям, получают теоретические (ожидаемые) частоты .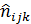
Рассмотрим пример реализации логлинейного анализа в ППП STATISTICA с последующей интерпретацией результатов. Задача состоит в оценке факторов риска развития артериальной гипертензии. Анализировалась частота встречаемости следующих признаков (факторов)
Таблица 76. Факторы риска
| Имя переменной | Расшифровка |
| АГ | 1 – есть АГ, 2 – нет АГ |
| Курение | не курит 1, курит 2 |
| Потребление алкоголя | не потребл. – 1, потребл. 2 |
| Потребление соленой пищи | не потребл. – 1, потребл. 2 |
| Наследственный фактор АГ | нет 1, есть 2 |
Исходные данные представляются в виде матрицы n×m, где n количество обследованных, mчисло признаков. Фрагмент этой матрицы показан в таблице 77. Общий объем выборки составил 607 человек.
Таблица 77. Данные к примеру
| № | Курение | Потр.Алког. | Потр. сол.пищи | Наследств (АГ) | АГ |
| … | … | … | … | … | … |
Если какието ячейки таблицы сопряженности окажутся пустыми – не встречается данное сочетание факторов, то программа автоматически вставляет в эту ячейку величину 0,5, что никак не влияет на конечные результаты.
Анализ проводится в модуле Nonlinear Estimation, для запуска которого надо в меню Statistics выбрать команду Advanced Linear/Nonlinear Models (линейные/нелинейные модели). В открывшемся меню выбрать команду Nonlinear Estimation (нелинейная оценка), а затем опцию LogLinear analysis of Frequency Tables (логлинейный анализ) – «ОК».
В открывшемся окне необходимо указать форму задания исходных данных input file Raw Data, и выбрать переменные из списка, щелкнув кнопкой Variables: в нашем примере отмечаем все признаки (факторы). Нажмите ОК. В открывшемся окошке LogLinear model specification вы увидите, что фактор курения имеет код 1, потребление алкоголя 2, потребление соли 3, наследственный фактор 4, наличие гипертонии (АГ) – 5.
Нажмите на кнопку Tests of Marginal and Partial Association (проверка общих и частных взаимосвязей), появятся две таблицы. Первая из них «Results of Fitting all KFactor Interactions», показывает результаты проверки нулевой гипотезы о независимости числа случаев от факторов и их сочетания. Проверка осуществляется по критерию максимального правдоподобия и по критерию хиквадрат Пирсона (таблица 78).
Таблица 78. Результаты статобработки
| Results of Fitting all KFactor Interactions These are simultaneous tests that all KFactor Interactions are simultaneously Zero. | |||||
| Degrs.of Freedom (число ст.св.) | Max.Lik.Chisqu.(критерий макс. правдоподобия) | Probab.p (руровень) | Pearson Chisqu (хиквадрат Пирсона) | Probab.p (руровень) | |
| KFactor | |||||
| 1 | 5 | 704,4 | 0,000 | 1548 | 0,000 |
| 2 | 10 | 206,2 | 0,000 | 237 | 0,000 |
| 3 | 10 | 6,7 | 0,754 | 6 | 0,798 |
| 4 | 5 | 4,3 | 0,511 | 4 | 0,527 |
| 5 | 1 | 0,9 | 0,342 | 1 | 0,344 |
При К=1 и 2 р<0,05, т.е. влияние самих факторов и их попарных сочетаний статистически значимо, а сочетания по 3, 4 и 5 факторов – незначимо.
Во второй таблице «Tests of Marginal and Partial Association» представлены данные о связи факторов и их сочетаний с ожидаемыми частотами наблюдений (рассчитанными по логлинейной модели) (таблица 79). Из нее видно, что статистически значимыми являются 9 эффектов (р<0,05 по критерию максимального правдоподобия и по критерию хиквадрат Пирсона).
Таблица 79. Результаты статобработки
| tests of Marginal and Partial Association | |||||
| Effect | Degrs.of Freedom (число ст.св.) | Prt.Ass. Chisqr. (частные взаимосв., хиквадрат) | Prt.Ass. P (частные взаимосв., руровень) | Mrg.Ass. Chisqr. (общие взаимосв., хиквадрат) | Mrg.Ass. P (общие взаимосв., руровень) |
| 1 | 1 | 209,8 | 0,000 | 209,8 | 0,000 |
| 2 | 1 | 141,4 | 0,000 | 141,4 | 0,000 |
| 3 | 1 | 178,2 | 0,000 | 178,2 | 0,000 |
| 4 | 1 | 74,3 | 0,000 | 74,3 | 0,000 |
| 5 | 1 | 100,7 | 0,000 | 100,7 | 0,000 |
| 12 | 1 | 69,5 | 0,000 | 69,5 | 0,000 |
| 13 | 1 | 1,3 | 0,257 | 0,3 | 0,576 |
| 14 | 1 | 0,0 | 0,874 | 0,8 | 0,383 |
| 15 | 1 | 0,2 | 0,631 | 0,0 | 0,825 |
| 23 | 1 | 2,8 | 0,092 | 1,5 | 0,221 |
| 24 | 1 | 10,6 | 0,001 | 10,9 | 0,001 |
| 25 | 1 | 0,3 | 0,585 | 0,3 | 0,567 |
| 34 | 1 | 0,3 | 0,593 | 3,2 | 0,076 |
| 35 | 1 | 8,5 | 0,004 | 11,7 | 0,001 |
| 45 | 1 | 106,5 | 0,000 | 109,6 | 0,000 |
| 123 | 1 | 0,9 | 0,346 | 1,3 | 0,263 |
| 124 | 1 | 0,1 | 0,758 | 0,3 | 0,577 |
| 125 | 1 | 1,6 | 0,201 | 2,3 | 0,128 |
| 134 | 1 | 0,0 | 0,880 | 0,0 | 0,899 |
| 135 | 1 | 0,6 | 0,440 | 0,8 | 0,384 |
| 145 | 1 | 0,7 | 0,396 | 0,2 | 0,653 |
| 234 | 1 | 1,0 | 0,322 | 1,1 | 0,289 |
| 235 | 1 | 0,0 | 0,873 | 0,3 | 0,615 |
| 245 | 1 | 0,1 | 0,702 | 0,0 | 0,840 |
| 345 | 1 | 0,9 | 0,341 | 0,7 | 0,392 |
| 1234 | 1 | 0,6 | 0,449 | 0,6 | 0,457 |
| 1235 | 1 | 0,1 | 0,750 | 0,9 | 0,345 |
| 1245 | 1 | 0,2 | 0,665 | 0,4 | 0,550 |
| 1345 | 1 | 2,7 | 0,098 | 2,7 | 0,099 |
| 2345 | 1 | 0,0 | 0,978 | 0,1 | 0,722 |
Так как нас интересует фактор наличия артериальной гипертонии (код 5) и связь его с другими изучаемыми факторами из данной таблицы выберем статистически значимые взаимодействия – это 35 и 45.
О степени влияния того или иного фактора судят по отношению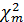 
данного фактора к сумме 
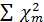всех факторов (в%) (таблица 80).
Таблица 80. Результаты статобработки
| Effect | Degrs.of Freedom | Prt.Ass. Chisqr. | Prt.Ass. p | % |
| 5 | 1 | 100,7 | 0,000 | 47 |
| 35 | 1 | 8,5 | 0,004 | 4 |
| 45 | 1 | 106,5 | 0,000 | 49 |
| Σ=215,7 |
Т.е. на 49% развитие артериальной гипертензии зависит от наследственных факторов, на 4% от излишнего потребления соли и на 47% от других факторов, которые не рассматриваются в данном исследовании.
Вернитесь в окошко LogLinear model specification и нажмите ОК.Появятся результаты автоматического поиска оптимальной модели для ожидаемых частот наблюдения (таблица 81).
Таблица 81. Результаты статобработки
| Table to be analyzed: (1) (2) (3) (4) (5) Курение Потр.Алк Потр. со Наследст АГ 2 x 2 x 2 x 2 x 2 Minimum cell frequency: 1, Maximum: 188, Sum: 607, Model to be tested: 21,53,42,54 Delta: ,5000 ; Maximum iterations: 50 ; Conv. criterion: ,0100 Convergence reached after 2 iterations df p Maximum Likelihood Chisquare: 16,269 22 ,80231 Pearson Chisquare: 15,922 22 ,81976 |
Оптимальной оказалась модель, включающая взаимодействия 21, 53, 42, 54. Значимость модели проверяется по критериям максимального правдоподобия и по критерию хиквадрат Пирсона. Нулевая гипотеза заключается в равенстве наблюдаемых и рассчитанных по модели ожидаемых частот. Т.к. р=0,8 (т.е.>0.05) нулевая гипотеза принимается и модель считается адекватной.
Более содержательный разбор наблюдавшихся частот можно провести, рассматривая таблицы 2×2 для попарного сочетания уровней факторов. Для этого нажмите кнопку Observed table (наблюдаемые частоты) и в появившемся окошке выберем, например, АГ и наследственный фактор. Появится 8 таблиц, первая из них (таблица 82)
Таблица 82. Результаты статобработки
| Obs. Freq. (+delta): АГ by Наследств (АГ) w/in vars: Курение:1 (нет) Потр.Алког.:1 (нет) Потр. сол.пищи:1 (нет) | |||
| Наследств фактор 1 (нет) | Наследств фактор 2 (есть) | Total | |
| АГ | |||
| 1 (есть) | 32,5 | 45,5 | 78 |
| 2 (нет) | 188,5 | 35,5 | 224 |
| Total | 221,0 | 81,0 | 302 |
Среди тех кто не курит, не пьет, не потребляет излишне соль гипертоники встречаются в 224/78=2,9 раза реже, чем здоровые. Причем среди гипертоников лиц с наследственным фактором в 45,5/35,5=1,3 больше, чем лиц без него.
Такой же анализ можно провести относительно других факторов и их сочетания.
Для задач прогнозирования используется опция Fitted table (ожидаемые частоты). Аналогично получаем таблицу 83
Таблица 83. Результаты статобработки
| Fitted Freq.: Потр. сол.пищи by АГ w/in vars: (ЛогитАГ) Курение:1 Потр.Алког.:1 Наследств (АГ):1 | |||
| Потр. сол.пищи 1 (нет) | Потр. сол.пищи 2 (да) | Total | |
| АГ | |||
| 1 (есть) | 22,1 | 45,0 | 67,1 |
| 2 (нет) | 38,8 | 9,7 | 48,5 |
| Total | 60,9 | 54,7 | 115,6 |
Если человек не курит, не потребляет алкоголь, не имеет наследственную отягощенность и не потребляет много соли, то вероятность АГ составляет 22,1/60,9*100%=36%, а его отсутствия 64%.