Поверхностный потенциал

ФИЗИКА ПОВЕРХНОСТИ

ПОЛУПРОВОДНИКОВ

Энергетический спектр электронов у поверхности кристаллов отличается от спектра объема из-за обрыва периодичности решетки (уровни Тамма), из-за адсорбции примесей поверхностью с образованием энергетических уровней примесей или химических соединений. Все эти состояния обычно расположены вблизи середины запрещенной зоны и выступают как центры рекомбинации или прилипания неравновесных носителей зарядов.

В зависимости от конкретных условий искривление зон у поверхности может привести к появлению области обогащения, обеднения или инверсии, т.е. к тем же эффектам, что и в случае эффекта поля. Степень искривления зон характеризуется поверхностным потенциалом j_s (рис. 9.1).

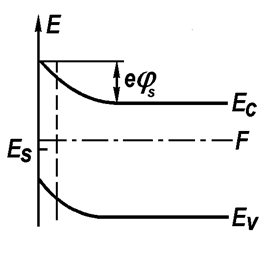
Рис. 9.1. Образование поверхностных состояний и искривление энергетических зон у поверхности полупроводника. Инверсия типа проводимости. Поверхностный потенциал j_s

Таблица 9.1

Знак заряда на поверхности полупроводника

Полупро- водник	Донор	Донор	Акцептор
O2	CO2	CO	H2O
Cu2O	–		+	+
CuO	–	–	+
NiO	–	–	+
Ge	–	+	+	+

Взаимодействие газов с поверхностными состояниями может сопровождаться физической или химической адсорбцией.

Физическая адсорбция – это силы Ван-дер-Ваальса порядка 0,01 – 0,1 эВ.

Химическая адсорбция – это обменное взаимодействие порядка 1 эВ, приводящее к образованию химических соединений.

Поверхностный потенциал

Рассмотрим полупроводник n-типа с обеднением поверхности. Пусть донорная примесь в объеме полностью ионизована и суммарный заряд равен нулю.

Уравнение электронейтральности:

n_o = N_d + p_o , (9.1)

объемный заряд r_o = 0.

Вблизи поверхности уравнение (9.1) не работает и объемный заряд:

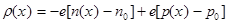, (9.2)

где 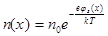; 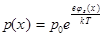(9.3)

– распределение Больцмана.

I. Для определения j(х) надо решить уравнение Пуассона:

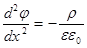, (9.4)

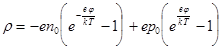(9.5)

Введем безразмерные обозначения:

; ;

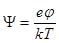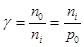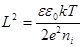
Если l > 0 в n-типе (характеризует степень легирования), то n_o > n_i, тогда уравнение Пуассона (9.4) примет вид:

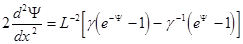(9.6)

Умножим обе части (9.6) на 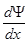и учтем:

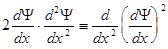
Тогда (9.4):

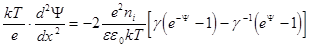(9.7)

После умножения на dx и интегрирования по dY:

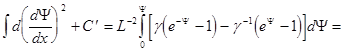
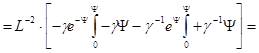
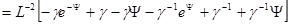(9.8)

Извлекая квадратный корень, получаем:

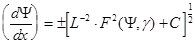, (9.9)

где 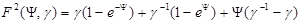(9.10)

Определим С из граничных условий: при 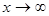, , 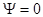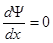; при этом 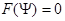и .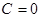

Окончательно:

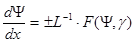(9.11)

В данном случае зоны изогнуты вверх ( 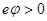), т.е. 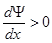(так как на поверхности энергия электронов больше, чем в объеме полупроводника):

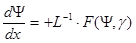(9.12)

Величину изгиба зон j_s можно найти:

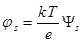(9.13)

II. Найдем связь Y_s с параметрами полупроводника из условия электронейтральности, ибо положительный заряд в приповерхностном слое Q_o равен отрицательному заряду на поверхностных уровнях Q_s:

Q_o = Q_s = en_s (9.14)

Полный отрицательный заряд на поверхностных уровнях:

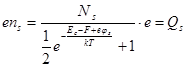(9.15)

С другой стороны, полный положительный заряд в приповерхностном слое из (9.4):

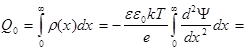
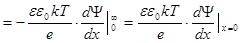(9.16)

Так как 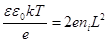, то заряд Q_o можно записать из (9.11):

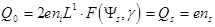(9.17)

В выражение n_s входит j_s, который можно найти из (9.12) и (9.13).

III. Распределение потенциала в области объемного заряда можно найти из (9.12):

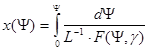(9.18)

Этот интеграл в общем виде не берется, обычно его рассматривают в трех областях: обогащения, обеднения и инверсии. Для каждого конкретного полупроводника функции L и F могут быть табулированы.