Плотность потока электромагнитного излучения

Билет

1) Линиями обозначены направления распространения электромагнитных волн. Линии, перпендикулярные поверхности, во всех точках которых колебания происходят в одинаковых фазах, называются лучами. А эти поверхности называются волновыми поверхностями.

Плотность потока электромагнитного излучения – это отношение электромагнитной энергии ∆W, проходящей через перпендикулярную лучам поверхность площадью S, за время ∆t, к произведению S на ∆t.
I = ∆W/(S*∆t)
Единицей измерения плотности магнитного потока в систему СИ являются ватты на квадратный метр (Вт/м^2). Выразим плотность потока через скорость его распространения и плотность электромагнитной энергии.
Возьмем поверхность S, перпендикулярную лучам. Построим на ней цилиндр с основанием c*∆t.
Здесь c – скорость распространения электромагнитной волны. Объем цилиндра вычисляется по формуле:
∆V = S*c*∆t.
Энергия электромагнитного поля сосредоточенного внутри цилиндра будет вычисляться по следующей формуле:
∆W = ∆V*ω.
Здесь ω - плотность электромагнитной энергии. Эта энергия за время ∆t пройдет через правое основание цилиндра. Получаем следующую формулу:
I = (ω*c*S*∆t)/(S*∆t) = ω*c.
Энергия по мере удаления от источника будет уменьшаться. Будет верна следующая закономерность, зависимости плотности тока от расстояния до источника. Плотность потока излучения направленного от точечного источника будет убывать обратно пропорционально квадрату расстояния до источника.
I = ∆W/(S*∆t) = ( ∆W/(4*pi∆t))*(1/R^2).
Электромагнитные волны излучаются при ускоренном движении заряженных частиц. При этом напряженность электрического поля и вектор магнитной индукции электромагнитной волны будут прямо пропорциональны. ускорению частиц.
Если рассматривать гармонические колебания, то ускорение будет прямо пропорционально квадрату циклической частоты. Полная плотность энергии электромагнитного поля будет равняться сумме плотности энергии электрического поля и энергии магнитного поля.
Согласно формуле I = ω*c, плотность потока пропорциональна полной плотности энергии электромагнитного поля.

Зависимость плотности потока излучения от расстояния до точечного источника.Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника.
Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4 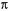R². Если считать, что источник по всем направлениям за время t излучает суммарную энергию W, то

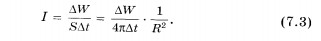
Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника.

Зависимость плотности потока излучения от частоты. Излучение электромагнитных волн происходит при ускоренном движении заряженных частиц (см. § 48). Напряженность электрического поля 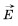и магнитная индукция 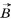электромагнитной волны пропорциональны ускорению 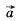излучающих частиц. Ускорение при гармонических колебаниях пропорционально квадрату частоты. Поэтому напряженность электрического поля и магнитная индукция также пропорциональны квадрату частоты:

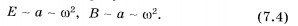
2) Дифракционная решётка - оптический прибор, предназначенный для анализа спектрального состава оптического излучения. Дифракционная решётка состоит из тысяч узких и близко расположенных щелей. Из-за интерференции интенсивность света прошедшего через дифракционную решётку различна в различных направлениях. Имеются выделенные направления в которых световые волны от различных щелей решётки складываются в фазе, многократно усиливая друг друга. При освещении решётки монохроматическим светом на её выходе наблюдаются узкие лучи с большой интенсивностью. Так как направления на интерференционные максимумы зависят от длины волны, белый свет , прошедший через дифракционную решётку, будет расщепляться на множество лучей разного цвета. Таким образом мы можем исследовать спектральный состав света. Выражение для интерференционных максимумов одинаково для пары щелей и дифракционной решётки, но в последнем случае максимум оказывается намного более острым и интенсивным, обеспечивая высокое разрешение в спектроскопических исследованиях.

ПРИМЕР: Один из простейших и распространённых в быту примеров отражательных дифракционных решёток — компакт-диск. На поверхности компакт-диска — дорожка в виде спирали с шагом 1,6 мкм между витками. Примерно треть ширины (0,5 мкм) этой дорожки занята углублением (это записанные данные), рассеивающим падающий на него свет, примерно две трети (1,1 мкм) — нетронутая подложка, отражающая свет.

3) Термоядерные реакции− реакции слияния (синтеза) лёгких ядер, протекающие при высоких температурах. Эти реакции обычно идут с выделением энергии, поскольку в образовавшемся в результате слияния более тяжёлом ядре нуклоны связаны сильнее, т.е. имеют, в среднем, бoльшую энергию связи, чем в исходных сливающихся ядрах. Избыточная суммарная энергия связи нуклонов при этом освобождается в виде кинетической энергии продуктов реакции. Название “термоядерные реакции” отражает тот факт, что эти реакции идут при высоких температурах (>10⁷–10⁸ К), поскольку для слияния лёгкие ядра должны сблизиться до расстояний, равных радиусу действия ядерных сил притяжения, т.е. до расстояний ≈10^-13 см. А вне зоны действия этих сил положительно заряженные ядра испытывают кулоновское отталкивание. Преодолеть это отталкивание могут лишь ядра, летящие навстречу друг другу с большими скоростями, т.е. входящие в состав сильно нагретых сред, либо специально ускоренные.

Реакция слияния ядер начинается тогда, когда сталкивающиеся ядра находятся в области их взаимного ядерного притяжения. Чтобы так сблизиться, сталкивающиеся ядра должны преодолеть их взаимное дальнодействующее электростатическое отталкивание, т.е. кулоновский барьер.

Кулоновский барьер- Атомные ядра имеют положительный электрический заряд. На больших расстояниях их заряды могут быть экранированы электронами. Однако для того, чтобы произошло слияние ядер, они должны сблизиться на расстояние, на котором действует сильное взаимодействие. Это расстояние — порядка размера самих ядер и во много раз меньше размера атома. На таких расстояниях электронные оболочки атомов (даже если бы они сохранились) уже не могут экранировать заряды ядер, поэтому они испытывают сильное электростатическое отталкивание. Сила этого отталкивания, в соответствии с законом Кулона, обратно пропорциональна квадрату расстояния между зарядами. На расстояниях порядка размера ядер величина сильного взаимодействия, которое стремится их связать, начинает быстро возрастать и становится больше величины кулоновского отталкивания.