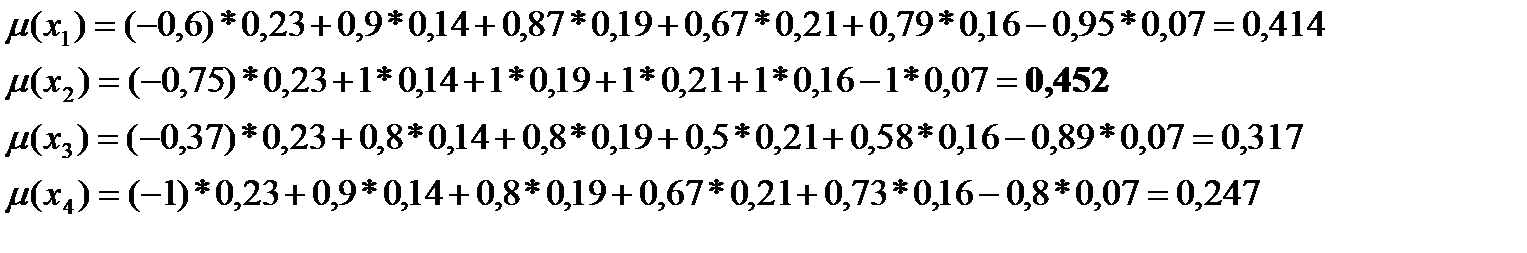Построение матрицы соответствий
Как уже отмечалось при принятии решений о выборе альтернативы среди конкурирующих альтернатив возникают трудности, в связи с тем, что исследуемые при экспертизе альтернативы характеризуются обычно многофакторной природой. Причем по одним параметрам альтернатива может отличаться от других в «лучшую» сторону, а по другим – в «худшую».
При большом количестве параметров задача ранжирования становится мало обозримой, поэтому нельзя использовать метод парных сравнений.
Обозначим через Х 
множество конкурирующих альтернатив, а через 
множество признаков, которыми характеризуется каждая альтернатива. Значение характеристик 
будем считать некоторыми числами, для обозначения которых будем использовать обозначение 
.
Построим для каждой альтернативы xi нечеткое множество Аi, определенное на универсальном множестве Y1, членами которого являются критерии yj конкурирующих альтернатив, а функция принадлежности 
нечеткого множества Аi количественно характеризует степень соответствия j-ого критерия и i-ой альтернативы.
Построим следующие матрицы:
| y1 | y2 | … | yp | |
| x1 | u11 | u12 | … | u1p |
| x2 | u21 | u22 | … | u2p |
| … | … | … | … | … |
| xn | un1 | un2 | … | unp |
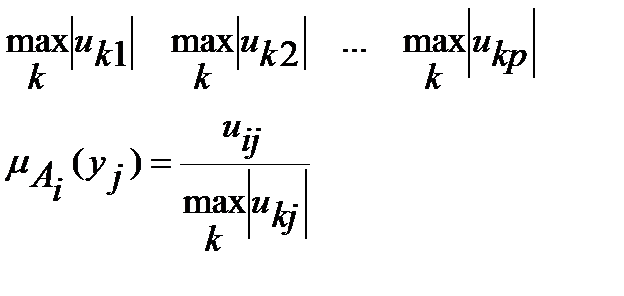
| y1 | y2 | … | yp | |
| x1 |  |  | … |  |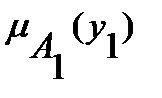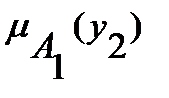
| x2 |  |  | … |  |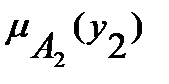
| … | … | … | … | … |
| xp |  |  | … |  |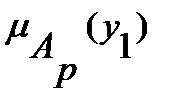
В этой матрице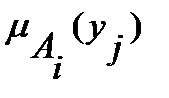 
указывает на степень соответствия i-ой альтернативы j-ому критерию. Последнюю матрицу мы будем называть матрицей соответствия альтернатив критериям.
показывает насколько y1 присутствует в 1-ой альтернативе х1.
Ранжирование конкурирующих альтернатив
На основе оценок, высказанных экспертами или используя оценки лица, принимающего решения, в виде балльных оценок, построим нечеткое множество В, имеющее конструкцию «свойство – степень важности свойства».
Сумма по i от 1 до p 
равна 1 – 
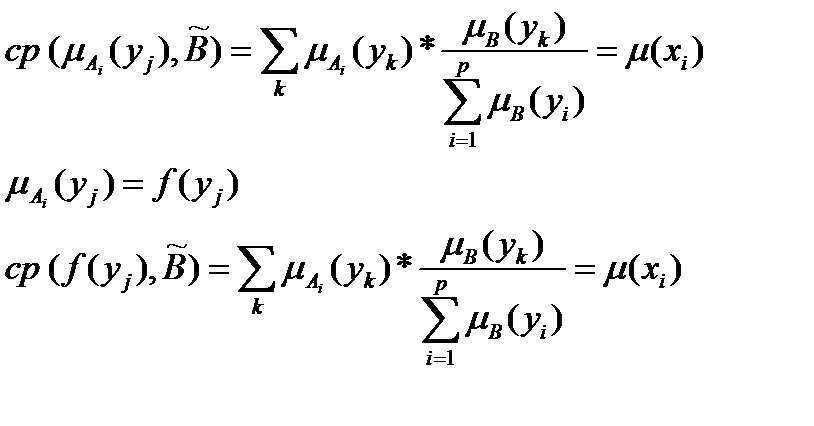
Функция принадлежности 
- это среднее значение степени принадлежности i-ой альтернативы по своим критериям требованиям лица, принимающего решения. Таким образом, для каждой альтернативы строится нечеткое множество, характеризующее присутствие каждого критерия в этой альтернативе.
Находим среднее значение присутствия критериев в каждой альтернативе с учетом важности критериев.
| y1 | y2 | … | yp | |
| x1 |  | | … | |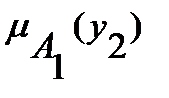
| x2 | | | … | |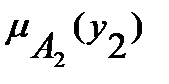
| … | … | … | … | … |
| xp | | | … | |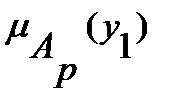
Критерий – это среднее значение функции принадлежности соответствующих характеристик в альтернативе по нечеткому множеству 
, функция принадлежности которого характеризует степень важности каждой характеристики.
Пример.
| № | Модель | Цена | Двухсимкартный | Дисплей | Процессор | ОЗУ | Емкость аккумулятора | Вес |
| Samsung Galaxy SM-J 120F | -8990 | + | 4,5 | -131 | ||||
| Samsung Galaxy SM-J 320F | -11290 | + | 1,5 | -138 | ||||
| Samsung Galaxy SM-J 105F | -5490 | + | 0,768 | -123 | ||||
| Samsung A3 SM-A300F | -14990 | + | 4,5 | -110 | ||||
| Максимальное значение | -14990 | + | 1,5 | -138 |
Критерий двухсимкартный можно опустить, так как у всех моделей смартфонов он присутствует.
Построим матрицу соответствия альтернатив критериям, для этого каждый элемент делим на максимальное значение по столбцам и проранжируем по степени важности каждый критерий в баллах от 1 до 10.
| № | Цена (y1) | Дисплей (y2) | Процессор (y3) | ОЗУ (y4) | Емкость аккумулятора (y5) | Вес (y6) |
| -0,6 | 0,9 | 0,87 | 0,67 | 0,79 | -0,95 | |
| -0,75 | -1 | |||||
| -5490 | 0,8 | 0,8 | 0,5 | 0,58 | -0,89 | |
| -0,37 | 0,9 | 0,8 | 0,67 | 0,73 | -0,8 | |
| Баллы |
Находим вес каждого критерия по нечеткому множеству В:
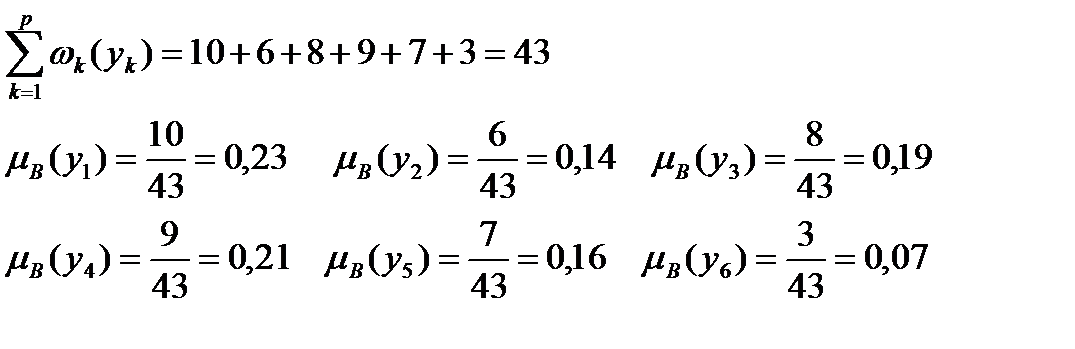
Находим функции принадлежности:
