Тема: «Метод парных сравнений»

В последние годы широкое развитие и применение получил метод парных сравнений, предложенный Т. Саатти.

Суть метода парных сравнений состоит в том, сто альтернативы сравниваются попарно и составляется матрица.

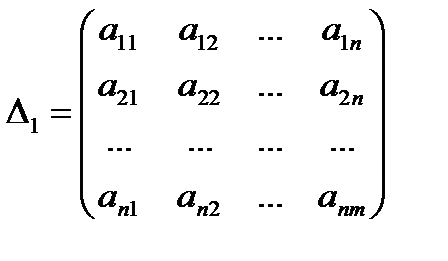(1)

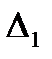– приближенное значение

где 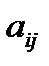указывает на то, во сколько раз i альтернатива «лучше» j.

Будем считать, что 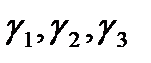- это истинные оценки альтернатив, которые мы не знаем, но хотим найти хотя бы приближенно.

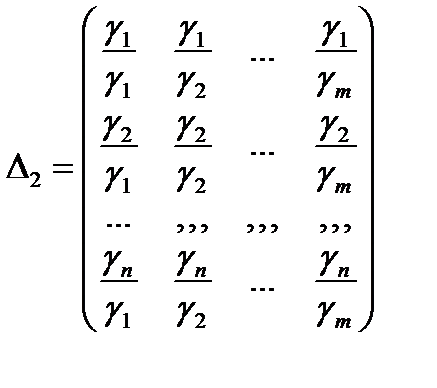– обратно симметричная матрица (2)

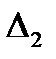- истинное значение

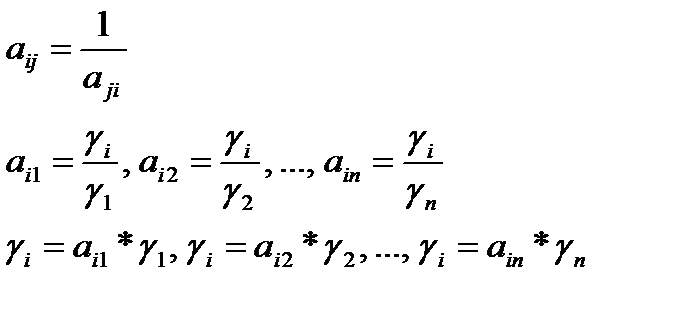
То, что 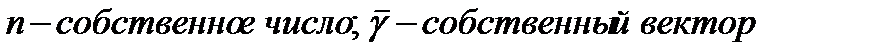, справедливо тогда, когда матрица 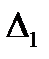будет совпадать с матрицей 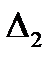и в этом случае матрица 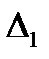называется согласованной.

Равенство 3 выполняется тогда, когда матрица 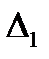и 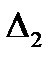совпадают и матрица 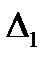в этом случае называется согласованной.

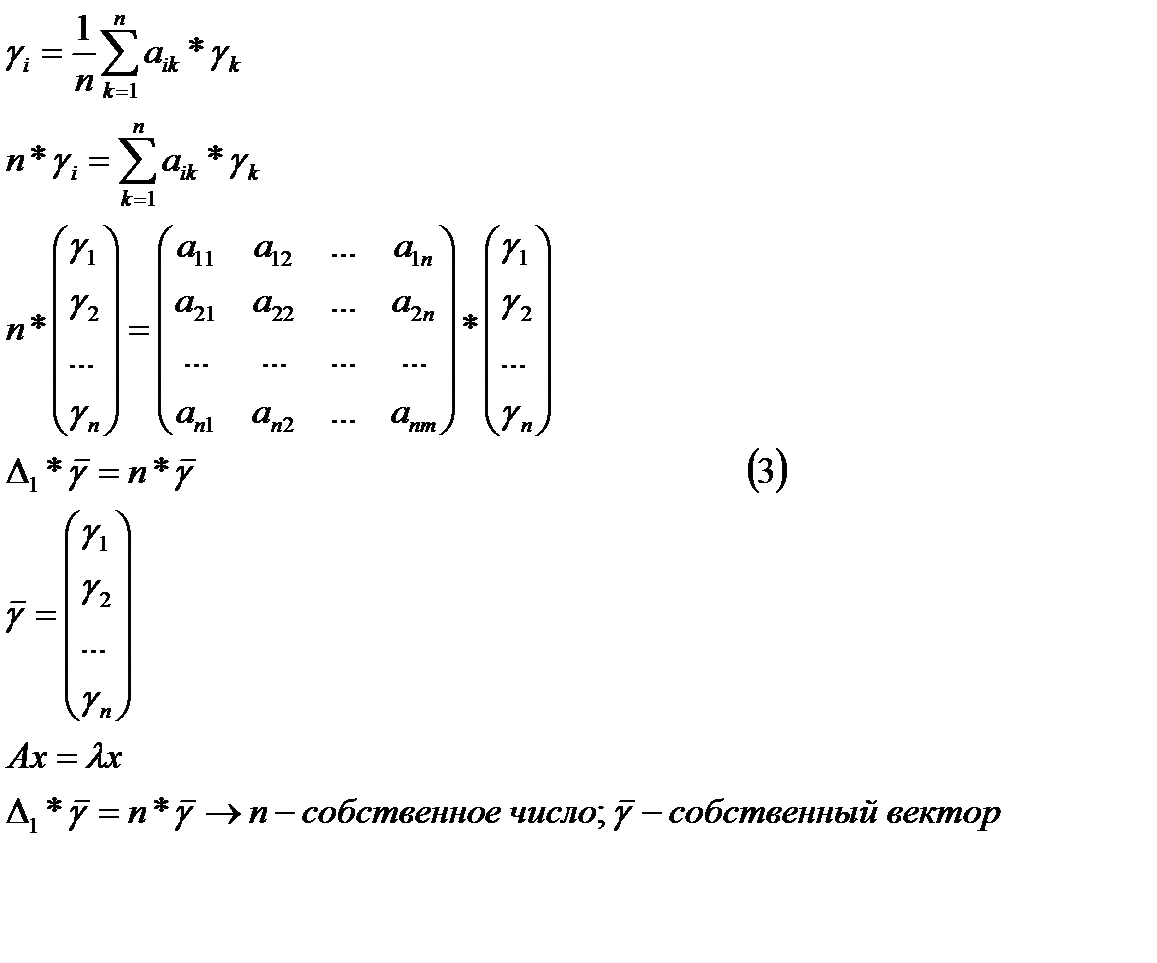
При согласованной матрице 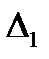n является собственным числом матрицы 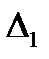, а вектор 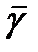собственным вектором матрицы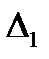

Отсюда вытекает следующий алгоритм поиска приближенного значения вектора 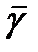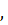ранжирующего альтернативу.

Так как матрица 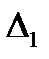как правило, не является согласованной, то она приближенно равна матрице 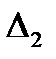, а поэтому собственные числа и собственные векторы матрицы 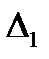близки к соответствующим собственным числам и собственным векторам матрицы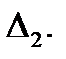

Тема: «Анализ методов парных сравнений (индекс согласованности; неустойчивость корней; достоинства проведения опросов в виде парных сравнений)»

Известно, что у матрицы 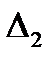собственные числа равны 0,0,…,0,n, поэтому у матрицы 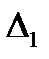будет n-1 собственное число мало отличающееся от нуля, а последнее число будет близким к n. Поэтому для ранжирования альтернатив находят собственные числа матрицы 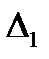выбирают среди них самое большое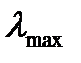 находят собственный вектор соответствующий максимальному собственному числу и по этому вектору ранжируют альтернативу.

Для оценки близости матрицы 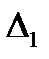парных сравнений используются отношения индекса согласованности:

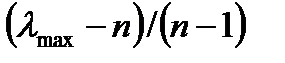
где 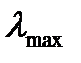- максимальное собственное число матрицы парных сравнений

n - ее порядок к случайному индексу матрицы соответствующего размера.

Если оценка согласованности не превосходит 0,1, то матрицу считают близкой к согласованной и в этом случае можно применять описанные процедуры.

Таблица – Значения случайных индексов для матриц различных порядков

Порядок матрицы	Случайный индекс	Порядок матрицы	Случайный индекс
	0,58		1,49
	0,90		1,51
	1,12		1,48
	1,24		1,56
	1,32		1,57
	1,41		1,59
	1,45

Описанный метод имеет существенные ограничения в применении, связанные с трудностями сравнения альтернатив, имеющих большое число параметров и, как следствие, трудностями получения согласованных матриц. Справедливости ради, необходимо отметить, что после появления метода парных сравнений появились и методы корректировки матрицы сравнений , позволяющие улучшить ее согласованность. Тем не менее, получить удовлетворительные результаты при решении производственных задач удается далеко не всегда.

Пример.

Задана матрица парных сравнений 3 альтернатив. Проверить согласованность этой матрицы, провести ранжирование этих альтернатив методом парных сравнений (методом Саатти).

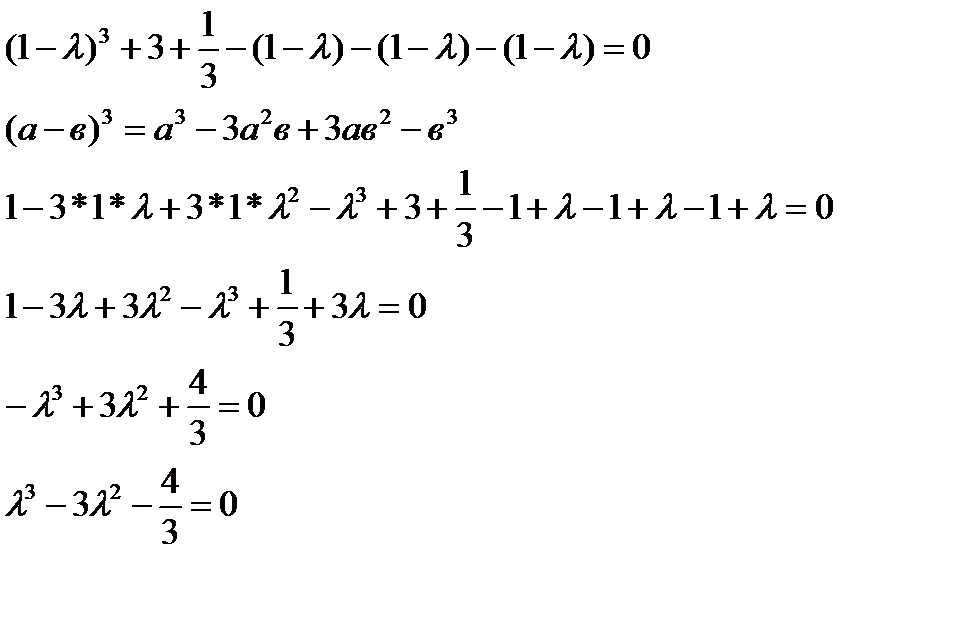
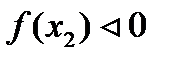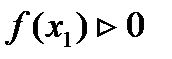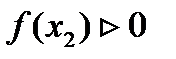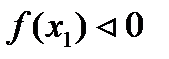3,136

3,1

3,15

+

-

2,8

3,2

+

+

+

-

3,1

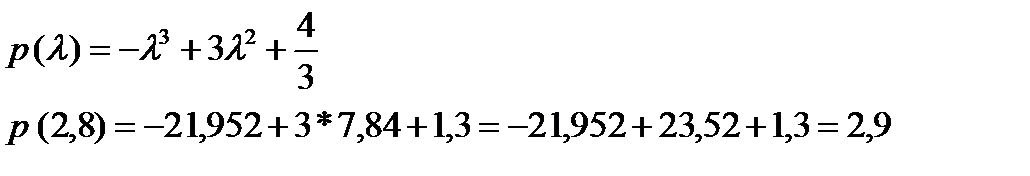
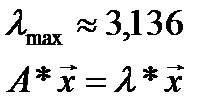
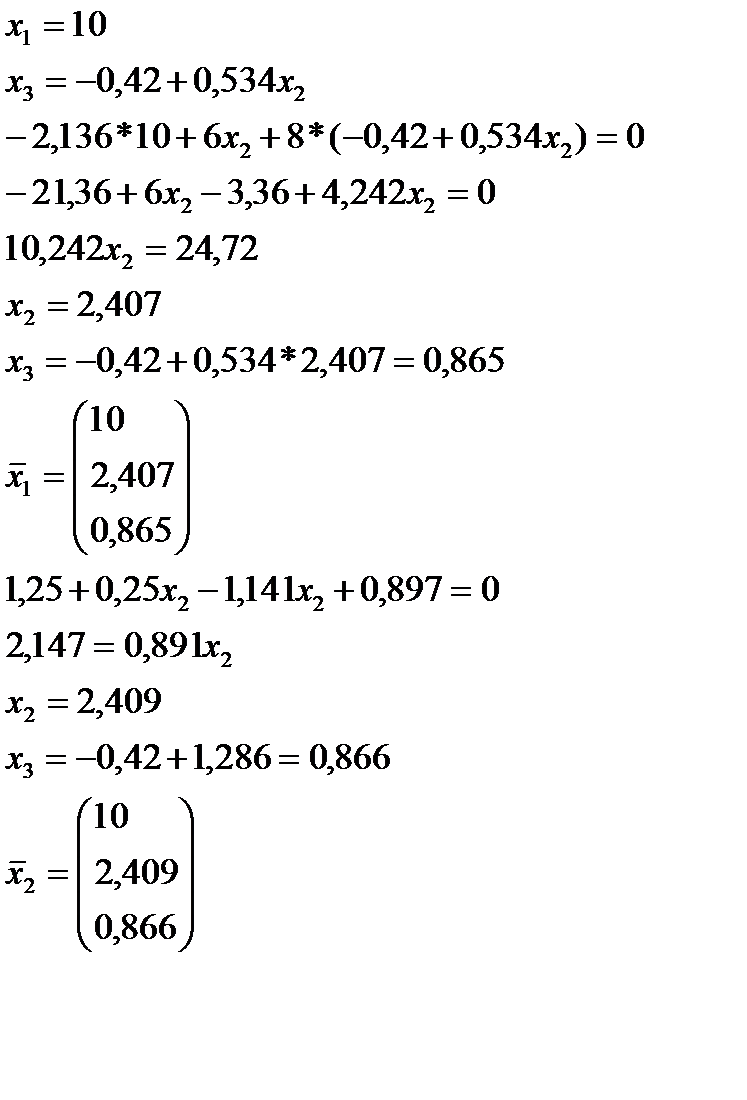
Индекс согласованности:

IC = 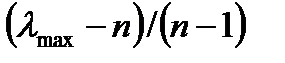= (3,136-3) / (3-1) = 0,068

Оценка согласованности:

ОС = 0,068 / 0,58 = 0,117