Справедливая цена опциона в простейшей модели
Доходы покупателя и продавца опциона зависят от колебаний цен на рынке, и они отражаются на премии. Если заранее известно, что цены будут, определённым образом, расти, то этот прирост должен войти целиком в премию. Наиболее важной является ситуация, в которой все известные тенденции в изменении цен уже учтены и оставшиеся колебания носят случайный характер.
Пусть цена акции в момент 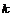 равна
равна 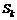 . Приращение цены
. Приращение цены  обозначим через
обозначим через  , тогда
, тогда
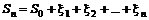
Предположим, что  - случайная величина со средним значением
- случайная величина со средним значением 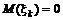 ,
,  .
.
В простейшей модели предположим, что величины  являются дискретными, т.е. могут принимать только два значения -
являются дискретными, т.е. могут принимать только два значения - 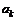 и
и 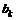 (
( 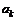 ,
, 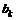 >0) с вероятностями соответственно
>0) с вероятностями соответственно 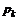 и
и  . Для вероятности должно выполняться
. Для вероятности должно выполняться 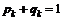 , а из равенства нулю математического ожидания имеем
, а из равенства нулю математического ожидания имеем  .
.
Получили систему

Решая её относительно 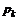 и
и  , находим
, находим
 ,
,
 .
.
Покажем теперь, что справедливой ценой опциона «колл» будет 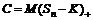 , где
, где  =
= 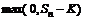 .
.
Действительно, если реальная премия 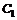 окажется меньше
окажется меньше  , то эмитент опциона не имеет возможности выполнить условие контракта без потерь. Докажем это для ситуации, когда
, то эмитент опциона не имеет возможности выполнить условие контракта без потерь. Докажем это для ситуации, когда  и цена исполнения равна начальной стоимости акции
и цена исполнения равна начальной стоимости акции  . Тогда
. Тогда
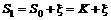 .
.
Находим справедливую цену
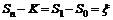 ,
,
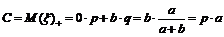 .
.
Предполагая, что 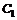 >
>  , докажем что эмитент может получить безрисковую прибыль в размере
, докажем что эмитент может получить безрисковую прибыль в размере  . После продажи опциона эмитент тут же покупает долю
. После продажи опциона эмитент тут же покупает долю 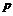 бумаг, указанных в опционе. Если в момент
бумаг, указанных в опционе. Если в момент 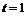 реализуется
реализуется  , то предъявлять опцион к исполнению не имеет смысла. Уменьшения цены акции на момент предъявления опциона создаст убыток в размере
, то предъявлять опцион к исполнению не имеет смысла. Уменьшения цены акции на момент предъявления опциона создаст убыток в размере 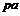 , тогда баланс эмитента составит
, тогда баланс эмитента составит  . Теперь рассмотрим случай, когда
. Теперь рассмотрим случай, когда  , то есть стоимость акции выросла, тогда опцион будет предъявлен к исполнению, и эмитент должен будет приобрести оставшуюся долю акций
, то есть стоимость акции выросла, тогда опцион будет предъявлен к исполнению, и эмитент должен будет приобрести оставшуюся долю акций 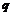 для покрытия опциона. Баланс его составит
для покрытия опциона. Баланс его составит 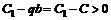 , что и требовалось доказать.
, что и требовалось доказать.
В процессе хеджирования после продажи опциона эмитент приобретает портфель из акций в объеме 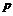 и облигаций на сумму
и облигаций на сумму 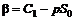 . Пара
. Пара  составляет пакет ценных бумаг. Только что было доказано, что этот портфель покрывает с избытком платежные обязательства
составляет пакет ценных бумаг. Только что было доказано, что этот портфель покрывает с избытком платежные обязательства 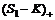 . Покажем, что если
. Покажем, что если 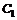 <
<  , то такого портфеля бумаг не существует. Пусть
, то такого портфеля бумаг не существует. Пусть 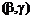 - произвольный портфель, сформированный эмитентом, состоящий из
- произвольный портфель, сформированный эмитентом, состоящий из  доли акций и облигаций на сумму
доли акций и облигаций на сумму 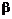 .
.
Пусть 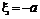 , тогда опцион не будет предъявлен к исполнению, а потери составят
, тогда опцион не будет предъявлен к исполнению, а потери составят 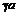 , баланс с учетом премии:
, баланс с учетом премии: 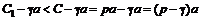 . Неотрицательный баланс возможен только когда
. Неотрицательный баланс возможен только когда  .
.
Пусть реализовалась 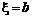 , тогда предъявление к исполнению опциона создаст убыток размера
, тогда предъявление к исполнению опциона создаст убыток размера 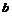 , а купленный пакет – доход в размере
, а купленный пакет – доход в размере  . Баланс составит:
. Баланс составит:
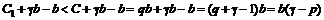 .
.
Это выражение неотрицательно в случае 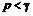 . Получили противоречие.
. Получили противоречие.
Только что рассматривался простейший случай так называемой биномиальной модели, так как возможны два положения: курс акций может пойти либо вверх («верхнее положение»), либо вниз («нижнее положение»).
Пример 4.2.1. Определить портфель ценных бумаг, воспроизводящий платежи по опциону «колл», и текущую стоимость опциона, если известно, что
| Ценные бумаги | «Верхнее» положение | «Нижнее» положение | текущий курс |
| Акция Облигация Опцион «колл» | 108,33 | 108,33 |
Определим состав портфеля, который точно повторит выплаты по опциону «колл». Рассмотрим портфель из  доля акций и
доля акций и 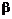 безрисковых облигаций. В «верхнем» положении такой портфель принесет выплаты в размере
безрисковых облигаций. В «верхнем» положении такой портфель принесет выплаты в размере 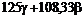 , в «нижнем» -
, в «нижнем» -  . Так как портфель полностью повторяет выплаты по опциону, то получаем систему:
. Так как портфель полностью повторяет выплаты по опциону, то получаем систему:
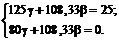
Решая её, получаем 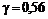 ,
, 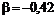 . Это означает, что инвестор может воспроизвести платежи по опциону «колл», осуществив короткую продажу безрисковых облигаций.
. Это означает, что инвестор может воспроизвести платежи по опциону «колл», осуществив короткую продажу безрисковых облигаций.
Текущая стоимость опциона равна
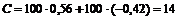 .
.
Изменение цены акции непременно приводит к изменению цены опциона. Данная взаимосвязь называется коэффициентом хеджирования опциона. Для выше рассмотренного случая биномиальной модели, когда цена акции анализируется лишь за один временной промежуток (  ) и может измениться лишь двумя способами, коэффициент хеджирования опциона «колл» определяется формулой:
) и может измениться лишь двумя способами, коэффициент хеджирования опциона «колл» определяется формулой:
 ,
,
где  ,
, 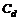 (
( 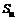 ,
, 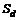 ) - цены опциона (акции) в «верхнем» и «нижнем» положениях соответственно.
) - цены опциона (акции) в «верхнем» и «нижнем» положениях соответственно.
Аналогичным образом определяется коэффициент хеджирования для опциона «пут»
 .
.
Упражнения
1. Определите состав воспроизводящего портфеля и текущую цену опциона, если известны следующие данные:
| Ценные бумаги | «Верхнее» положение | «Нижнее» положение | текущий курс |
| Акция Облигация Опцион «колл» | ? |
2. Текущий курс акции компании равен 50 долл. Через год эта акция будет стоить или 58,09 долл. или 43,64 долл. Непрерывно начисляемая годовая безрисковая процентная ставка равна 5,13%. Рассчитайте действительную стоимость опциона «колл» при цене исполнения 50 долл., если при этом до истечения остается один год.
3. Инвестор может воспроизвести платежи по опциону «колл», осуществив «короткую» продажу безрисковых облигаций на сумму 20 долл. Действительная стоимость опциона равна 5 долл. при цене исполнения 50 долл. Текущий курс акции равен 50 долл. Определить цену акции в «нижнем» положении через 6 месяцев, если годовая номинальная безрисковая процентная ставка равна 10%.
4. Найти неизвестную величину
| Ценные бумаги | «Верхнее» положение | «Нижнее» положение | текущий курс |
| Акция Облигация Опцион «колл» | ? |
5. Определить коэффициенты хеджирования опционов «колл» из задач 1 и 4.
6. Определить текущую стоимость «короткой» позиции по облигации в воспроизводящем портфеле, если коэффициент хеджирования равен 0,7, а текущие курсы акции и опциона соответственно 1000 и 300 р.
Биномиальная модель
В предыдущем параграфе рассматривался простейший случай биномиальной модели, когда курс акции анализировался в начале и в конце некоторого временного промежутка и мог изменяться лишь двумя способами.
Рассмотрим наиболее общие случаи биномиальной модели. Покажем, что расчет цены опциона для рынка с дискретным временем может быть проведен с помощью линейного программирования. Такая формулировка задачи имеет многочисленные достоинства, поскольку линейное программирование достаточно хорошо апробировано на практике. Ниже приводится постановка задачи ЛП для определения цены опциона и хеджирующей стратегии в полиномиальном случае, а также ее аналитическое решение для случая – когда количество возможных состояний равно двум или трем, а количество по времени – одному.
Предположим, что цена акции  может меняться лишь в моменты времени
может меняться лишь в моменты времени 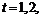 по законам
по законам
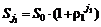
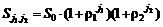 ,
,
где 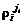 ,
, 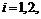 - независимо распределённые случайные дискретные величины, принимающие
- независимо распределённые случайные дискретные величины, принимающие 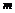 значений
значений  с некоторыми вероятностями. Как и в предыдущем случае, эти вероятности не влияют на цену опциона.
с некоторыми вероятностями. Как и в предыдущем случае, эти вероятности не влияют на цену опциона.
Пусть банковский счет растет по формуле сложных процентов
 ,
,
где 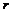 - постоянная процентная ставка.
- постоянная процентная ставка.
Пусть инвестор, оперирующий на рынке в момент времени  , обладает после продажи опциона начальным капиталом
, обладает после продажи опциона начальным капиталом 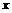 . Он может вложить некоторую его часть
. Он может вложить некоторую его часть 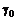 в акции, а оставшуюся,
в акции, а оставшуюся, 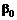 , поместить на банковский счет или вложить в «безрисковые» облигации:
, поместить на банковский счет или вложить в «безрисковые» облигации:
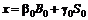 .
.
Можно поставить следующую инвестиционную задачу: не привлекая дополнительных источников финансирования, довести в момент времени  стоимость портфеля до величины не меньшей, чем заданная функция выплат
стоимость портфеля до величины не меньшей, чем заданная функция выплат 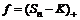 . Достичь этого инвестор может путем диверсификации портфеля: после того, как цена акции изменилась, он принимает решение о возможных изменениях значений
. Достичь этого инвестор может путем диверсификации портфеля: после того, как цена акции изменилась, он принимает решение о возможных изменениях значений 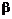 и
и  .
.
Все варианты цен акций можно наглядно представить в виде полиномиального дерева (для случая, когда число вариантов изменения цен 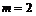 , а число шагов по времени
, а число шагов по времени 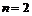 ). Каждому узлу соответствует цена акции
). Каждому узлу соответствует цена акции  в первый момент времени и
в первый момент времени и 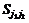
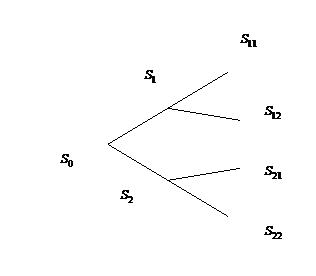
Рис. 4.3.1. Пример полиномиального дерева
Для этого случая задача ЛП принимает вид
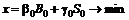 (4.3.1)
(4.3.1)
при условиях
 (4.3.2)
(4.3.2)
Это условия самофинансирования для момента времени 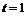 . Здесь в правых и левых частях равенств стоят величины капиталов соответственно до и после принятия решения. Величина капитала при этом не меняется, меняется лишь его доля, вкладываемая в акции и облигации. Будем считать, что
. Здесь в правых и левых частях равенств стоят величины капиталов соответственно до и после принятия решения. Величина капитала при этом не меняется, меняется лишь его доля, вкладываемая в акции и облигации. Будем считать, что 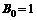 .
.
Для выполнения инвестиционной задачи должны выполняться следующие хедж-условия:
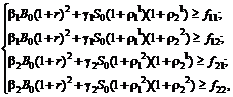 (4.3.3)
(4.3.3)
где 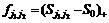 - функция выплат,
- функция выплат,  .
.
Естественно постараться выполнить условия при наименьшем начальном капитале 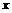 . Эта задача связана с определением рациональной стоимости опциона европейского типа.
. Эта задача связана с определением рациональной стоимости опциона европейского типа.
Выражая из условий (4.3.2) 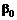 и
и 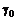 , (4.3.1) приведём к виду
, (4.3.1) приведём к виду
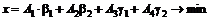 (4.3.4)
(4.3.4)
Для решения новой задачи (4.3.3. - 4.3.4.) перейдем к двойственной, которая имеет следующий вид:
 ,
,

Решая полученную задачу симплекс-методом или любым другим возможным способом, находим оптимальную цену опциона.
Пример 4.3.1. В начале 2004 года цена акции была 10 долл. По прогнозам экспертов в конце 2004 и 2005 годов она может вырасти или упасть на 50 % с равными вероятностями. Определить цену опциона в конце 2005 года. Банковская годовая процентная ставка равна 10%.
Решение.
Цена опциона определяется формулой
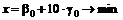 . (4.3.5)
. (4.3.5)
Условия самофинансирования имеют вид:

Хедж-условия имеют вид:

Выражая из условий самофинансирования 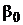 и
и 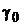 и подставляя полученные выражения в (4.3.5), получаем
и подставляя полученные выражения в (4.3.5), получаем
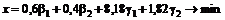 .
.
Переходим к двойственной задаче.
 ,
,

Находим решение полученной системы  .
.
Итак, цена опциона равна 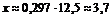 .
.
Аналогичным образом, можно решать задачу определения цены опциона в биномиальной модели для произвольного конечного числа моментов времени.
Предположим теперь, что на каждых торгах цена акции может изменяться только в 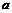 ,
, 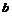 и
и 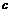 раз, и решим задачу о цене опциона в случае
раз, и решим задачу о цене опциона в случае  . Соответствующая задача ЛП имеет вид
. Соответствующая задача ЛП имеет вид
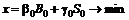
при хедж-условиях
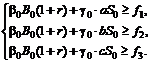
Для её решения перейдем к двойственной задаче, которая выглядит следующим образом:
 ,
,
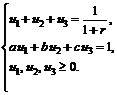
Аналогично предыдущей задаче можно найти справедливую цену опциона.
Пример 4.3.2. В начале 2004 года цена акции была 10 долл. По прогнозам экспертов в конце 2004 года она может изменить в 0,8, 1,2 и 1,5 раз с равными вероятностями. Определить цену опциона в конце 2004 года. Банковская годовая процентная ставка равна 10%.
Решение. Цена опциона определяется формулой
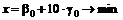 .
.
Хедж-условия имеют вид:

Переходим к двойственной задаче.
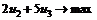 , (4.3.6)
, (4.3.6)

Находим решение полученной системы 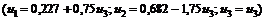 . Подставляем его в (4.3.6)
. Подставляем его в (4.3.6)
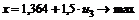 .
.
Так как  , то
, то
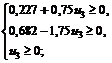
или  . Значит, цена опциона равна
. Значит, цена опциона равна  .
.
Итак, видно, что применение линейного программирования имеет многочисленные достоинства и упрощает задачу расчета цены опциона.
Упражнения
1. 1 января цена акции была 10 долл. По прогнозам экспертов 31 января цена акции может с равными вероятностями возрасти до 12 долл. или упасть до 8 долл., а затем 28 февраля снова увеличиться или уменьшиться на 50%. Определить цену опциона в конце февраля, если банковская годовая номинальная процентная ставка равна 12%, а цена исполнения 10 долл.
2. Текущая цена опциона на акции стоимостью и ценой исполнения 25 долл. равна 5 долл. Есть вероятность, что через год цена акции поднимется или упадет на 20% или останется неизменной. Стоит ли эмитенту продавать этот опцион, если годовой банковский процент равен 0,12? Почему?
3. Если цена акции стоимостью 1000 р. в начале года может измениться в 0,6, 0,9 и 1,3 раза к концу этого года, то какова оптимальная цена опциона «колл» на эту акцию на начало года? Банковский процент равен 8%. Каким будет доход покупателя этого опциона в каждом из возможных случаев? Почему?
4. Аналитики в области финансов отметили, что цена акций крупной компании в конце каждого года увеличивается или уменьшается на 10%. Определить цену опциона в начале 2000 года с ценой исполнения 11 долл., датой истечения 2 года. Текущая стоимость акции равна 10 долл., банковская процентная ставка 8 %.
5. Цена акции через год является дискретной случайной величиной, имеющей следующий закон распределения:
| Х | |||
| Р | 0,3 | 0,2 | 0,5 |
Определите величину безрисковой прибыли эмитента опциона «колл», если текущая цена этого опциона с датой исполнения один год и ценой исполнения 120 долл. равна 30 долл. Текущая стоимость опциона равна 120 долл., а банковский годовой процент 10%. Изобразить графически зависимость доходов покупателя и продавца от стоимости акции на момент предъявления опциона.
Модель Блэка-Шоулза
Если число периодов до даты истечения возрастет, то в этом случае биномиальная модель превращается в модель Блэка-Шоулза, названную так в честь ее авторов.
В условиях отсутствия налогов и трансакционных издержек стоимость опциона «колл» можно оценить, воспользовавшись формулой, предложенной Блэком и Шоулзом:
 ,
,
где
 , (4.4.1)
, (4.4.1)
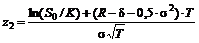 , (4.4.2)
, (4.4.2)
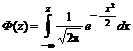 .
.
Здесь  - время до истечения, в годах,
- время до истечения, в годах,  - непрерывно начисляемая ставка без риска в расчете на год,
- непрерывно начисляемая ставка без риска в расчете на год, 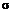 - риск базисной обыкновенной акции, измеренный стандартным отклонением доходности акции, представленной как непрерывно начисляемый процент в расчете на год,
- риск базисной обыкновенной акции, измеренный стандартным отклонением доходности акции, представленной как непрерывно начисляемый процент в расчете на год, 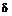 - непрерывно начисленные дивиденды по акциям.
- непрерывно начисленные дивиденды по акциям.
Очевидно из (4.4.1) и (4.4.2), что
 .
.
Пример 4.4.1. Цена акции в настоящий момент равна 475 рублей. Стандартное отклонение 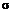 =12% в год. Акция выплачивает дивиденды с интенсивностью 5%. Интенсивность для краткосрочных облигаций 10%. Определить цену опциона на покупку акции с ценой исполнения 480 рублей через 3 месяца.
=12% в год. Акция выплачивает дивиденды с интенсивностью 5%. Интенсивность для краткосрочных облигаций 10%. Определить цену опциона на покупку акции с ценой исполнения 480 рублей через 3 месяца.
Решение.  =475,
=475, 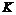 =480,
=480,  =0,1,
=0,1,  =0,25,
=0,25, 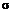 =0,12,
=0,12, 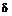 =0,05.
=0,05.
Имеем
 ,
,
 .
.
Согласно модели Блэка-Шоулза цена опциона равна

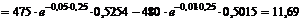 .
.
Итак, цена опциона на данную акцию равна 11,69 рублей.
Опционы «колл» и «пут» на одну и ту же бездивидендную акцию с текущей стоимостью  , одинаковой ценой исполнения и датой истечения связаны формулой (4.1.3). Для дивидендной акции эта формула примет вид
, одинаковой ценой исполнения и датой истечения связаны формулой (4.1.3). Для дивидендной акции эта формула примет вид
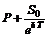 =
=  .
.
Тогда согласно модели Блэка-Шоулза стоимость опциона «пут» составит
 =
= 
 =
=  +
+ 
 =
=
=  .
.
Упражнения
1. Опцион «колл» истекает через три месяца и имеет цену исполнения 40 долл. Текущий курс и риск бездивидендной обыкновенной акции составляет 36 долл. и 50% соответственно, а непрерывно начисляемая ставка без риска 5%. Определить цену опциона.
2. Определить стоимость четырехмесячного опциона «колл» на акцию с постоянной непрерывной дивидендной доходностью 4% при цене исполнения 350 долл., если текущая стоимость равна 348 долл., интенсивность для краткосрочных облигаций 7% и среднеквадратическое отклонение доходности акции 30%.
3. Рассчитать с помощью формулы Блэка-Шоулза внутреннюю изменчивость акции без дивидендов для трехмесячного опциона «колл» с текущей премией 8,54, стоимостью базисного актива 83 долл., ценой исполнения 80 долл. Непрерывно начисленная безрисковая процентная ставка 5%.
4. Использую модель Блэка-Шоулза определить стоимость девятимесячного европейского опциона «колл» на акцию стоимостью 750 долл. и ценой исполнения 750 долл. Непрерывно начисляемая безрисковая процентная ставка 9%, постоянная дивидендная доходность равна 7%, а среднеквадратическое отклонение доходности акции составляет 4%.
5. Используя условие 2 задачи определить стоимость опциона «пут».
6. Рассчитайте на основе нижеприведенных данных с помощью модели Блэка-Шоулза цену годового опциона «пут» на бездивидендную акцию:
 =3200 р.,
=3200 р., 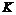 =4500 р.,
=4500 р.,  =0,06,
=0,06, 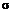 =0,35.
=0,35.
Ответы
Глава 4
§4.1.
1. 80 р., -50 р. 2. -5 долл. 3. а) - 900 р.; б) 400 р.; в) -100 р. 4. а) 900 р.; б) - 400 р.; в) 100 р. 5. 5 долл. 6. 533 р., 5300 р.
§4.2.
1. (0,7, -0,57), 20,3. 2. 4,87 долл. 3. 42 долл. 4. 1036. 5. 0,7, 0,67. 6. 400 р.
§4.3.
1. 2, 57 долл. 2. стоит. 3. 190 р., -190 р., -190 р., 110 р. 4. 0,76 долл. 5. 6,4 долл.
§4.4.
1. 2,26 долл. 2. 24,4 долл. 3. 40%. 4. 16 долл. 5. 22,9 долл. 6. 1191 р.
Приложение
