Последовательность независимых испытаний. Схема Бернулли
Если события, связанные с различными испытаниями, являются причинно-независимыми, то вышеописанный составной эксперимент называется последовательностью независимых испытаний. В математической модели такой последовательности соответствующие события должны быть независимы и в теоретико-вероятностном смысле.
Последовательность независимых испытаний иногда называют схемой независимых испытаний или полиномиальной схемой.
Пусть в каждом независимом испытании может наступить один из 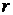 исходов, причем их вероятности не зависят то номера испытания (однородная схема). Вероятность
исходов, причем их вероятности не зависят то номера испытания (однородная схема). Вероятность  того, что в
того, что в  испытаниях полиномиальной схемы исход «1» наступил
испытаниях полиномиальной схемы исход «1» наступил 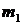 раз, исход «2» –
раз, исход «2» –  раз, …, исход «r» –
раз, …, исход «r» –  раз, будет тогда определяться равенством (полиномиальной формулой)
раз, будет тогда определяться равенством (полиномиальной формулой)
 , (15)
, (15)
где  – вероятность
– вероятность 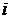 -го исхода в отдельном испытании
-го исхода в отдельном испытании  ;
; 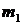 ,
,  , …,
, …, 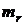 – целые неотрицательные числа, удовлетворяющие равенству
– целые неотрицательные числа, удовлетворяющие равенству 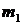 +
+  + …+
+ …+ 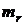 =
=  .
.
Пример. Найти вероятность того, что среди 20 случайно выбранных цифр имеется ровно 10 четных цифр, две «тройки» и три «семерки».
◄ Для вычисления искомой вероятности данный опыт представим как последовательность 20 независимых испытаний, в каждом из которых возможно появление одного из четырех исходов: 1 – четная цифра, 2 – тройка, 3 – семерка, 4 – все остальное. Вероятности этих исходов равны соответственно  ,
, 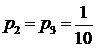 ,
, 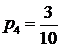 (
(  ). По формуле (15) получим
). По формуле (15) получим
 .►
.►
На практике часто приходится рассматривать последовательности с двумя исходами ( 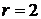 ): прибор за рассматриваемый период времени работал нормально или отказал; изделие оказалось годным или дефектным; на лотерейный билет получен выигрыш или нет и т. д.
): прибор за рассматриваемый период времени работал нормально или отказал; изделие оказалось годным или дефектным; на лотерейный билет получен выигрыш или нет и т. д.
Частный случай последовательности независимых испытаний, в котором каждое испытание может закончиться одним из двух исходов, называют схемой Бернулли. Обычно один из этих исходов условно называют «успехом» (исход  ), а другой – «неудачей» (исход
), а другой – «неудачей» (исход 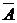 ), а их вероятности обозначают
), а их вероятности обозначают 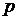 (
(  ) и
) и  соответственно. Для схемы Бернулли часто представляет интерес событие
соответственно. Для схемы Бернулли часто представляет интерес событие  ={в
={в  испытаниях наступило ровно
испытаниях наступило ровно 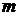 успехов}. Вероятность этого события определяется формулой (формулой Бернулли)
успехов}. Вероятность этого события определяется формулой (формулой Бернулли)
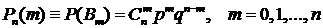 , (16)
, (16)
которая получается из формулы (15), если положить 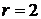 ,
,  ,
,  . В частности, вероятность того, что событие
. В частности, вероятность того, что событие  («успех») произойдет во всех
(«успех») произойдет во всех  испытаниях,
испытаниях, 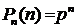 , а вероятность того, что он не произойдет ни разу,
, а вероятность того, что он не произойдет ни разу,  .
.
Пример. Система, состоящая из 10 блоков, сохраняет работоспособность, если за рассматриваемый период времени выйдет из строя не более двух блоков, Найти вероятность безотказной работы системы в предположении, что отказы блоков являются независимыми событиями и вероятность отказа каждого блока равна 0,1.
◄ В качестве модели используем схему Бернулли с 10 испытаниями. Каждое испытание заключается в работе одного из блоков за рассматриваемый период. Назовем «успехом» выход блока из строя. Нас интересует событие  ={система работает безотказно}. Тогда
={система работает безотказно}. Тогда  , где ={из строя вышло блоков}. Используя формулу (16), получим
, где ={из строя вышло блоков}. Используя формулу (16), получим
.►
Вероятность , определяемая формулой (16), есть функция целочисленного аргумента . Поведение этой функции следующее: она в начале при возрастании возрастает, достигает максимума, а затем убывает. Наиболее вероятное число успехов (наивероятнейшее число) (т. е. число, для которого для всех =0, 1, 2, …, ) находится из двойного неравенства .
Пример. В схеме Бернулли вероятность исхода («успеха») равна 3/5. Найти число наступлений исхода , имеющего наибольшую вероятность, если число испытаний равно а) 19, б) 20.
◄ При =19 имеем , а . Таким образом, максимальная вероятность достигается при двух значениях , равных 11 и 12.
При =20 находим , а . Поскольку не является целым числом, то будем иметь единственное максимальное значение вероятности при =12, которое больше , но меньше . ►
