Вычисление площадей плоских фигур.

1) Функция неотрицательна и непрерывна на [a, b]. Тогда по геометрическому смыслу определённого интеграла площадь S под кривой на (см. рис.) численно равна определённому интегралу:

2) Функция и непрерывна на . Тогда площадь над кривой на равна

3) Функция общего вида на . Пусть исходный отрезок можно разбить на конечное число интервалов, в каждом из которых имеет постоянный знак или равна нулю (см. рис.):

Тогда площадь фигуры равна

4) Теорема.Пусть на заданы непрерывные функции и , Тогда площадь фигуры между кривыми и на равна (см. рис.):

Вычисление объёмов тел вращения.

Пусть на задана непрерывная знакопостоянная функция . Объем тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями , , , (см. рис.):

По аналогии можно записать формулу для объёма тела, образованного вращением вокруг оси криволинейной трапеции, образованной линиями , , , :

Приближенное вычисление определённых интегралов.

Использование формулы Ньютона-Лейбница не всегда возможно, поскольку не всегда можно найти первообразную подынтегральной функции. Поэтому на практике используются так называемые численные методы, позволяющие найти приближённое значение интеграла с требуемой точностью. Такой подход предпочтителен ещё и потому, что возможности вычислительной техники непрерывно возрастают.

Рассмотрим один из таких методов – формулу трапеций.Пусть на задана непрерывная неотрицательная функция . Тогда, если отрезок разбить на равных отрезков, каждый длиной , формула трапеций имеет вид:

,

где , , ;

Погрешность формулы трапеций равна

где S(n) – правая часть формулы трапеций, Формула трапеций тем точнее, чем меньше шаг разбиения h.

Тема 13 Дифференциальные уравнения первого порядка

Лекция 13. 1 «Дифференциальные уравнения первого порядка»

Учебные вопросы:

1. Обыкновенные дифференциальные уравнения. Основные понятия

2. Уравнения первого порядка с разделяющимися переменными

3. «Однородные» уравнения первого порядка

4. Линейные уравнения первого порядка

Обыкновенные дифференциальные уравнения. Основные понятия

При рассмотрении неопределенного интеграла решалась задача: найти функцию , если (или, что то же самое, ), где – известная функция. Общее решение этой задачи, как уже известно, дается формулой , и сводится, таким образом, к вычислению неопределенного интеграла.

Более сложная задача: найти функцию , если известно, что она удовлетворяет заданному соотношению вида

(5.1)

Такого рода соотношения, связывающие независимую переменную , неизвестную функцию и ее производные до некоторого порядка, называются обыкновенными дифференциальными уравнениями (далее – дифференциальные уравнения или, просто, уравнения). Дифференциальные уравнения позволяют выразить соотношения между изменениями величин, и поэтому имеют большое значение в приложениях.

Решение (интегрирование) дифференциального уравнения (5.1) заключается в отыскании функций (решений, интегралов) , которые удовлетворяют этому уравнению для всех значений в определенном конечном или бесконечном интервале . Решения могут быть проверены подстановкой в уравнение.

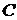Пример. Проверить, что все функции вида , где – произвольная постоянная, принимающая любые значения от 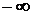до 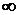, удовлетворяют дифференциальному уравнению .

◄ Находим первую производную: . Подставляя 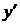и в исходное уравнение, получаем тождество , т. е. данные функции удовлетворяют уравнению (являются его решениями). ►

Порядок наивысшей производной, входящей в дифференциальное уравнение, называется порядком этого дифференциального уравнения.

Примеры:

· ― уравнение 1-ого порядка,

· ― уравнение 2-ого порядка,

· ― уравнение 5-ого порядка.

Решение простейшего дифференциального уравнения -ого порядка

(5.2)

можно получить с помощью интегрирований.

Пример. Найти решение простейшего дифференциального уравнения 3-ого порядка

◄ Интегрируя, последовательно находим:

;

;

.

Таким образом, решение данного дифференциального уравнения имеет вид , где – произвольные постоянные, никак между собой не связанные. ►

Общее решение дифференциального уравнения порядка имеет вид

. (5.3)

где – произвольные постоянные (постоянные интегрирования). При решении дифференциальных уравнений нередко приходят к выражению вида , не разрешенному относительно (неявно заданная функция). Такое выражение, неявно задающее общее решение, называют общим интегралом дифференциального уравнения (а собственно интегралы – квадратурами).

Каждый частный выбор постоянных в общем решении (интеграле) дает частное решение (интеграл) дифференциального уравнения.

Пример. Для рассмотренного выше уравнения частными решениями будут

.

В задаче Коши (начальной задаче) требуется найти частное решение (интеграл), удовлетворяющее начальным условиям

, (5.4)

по которым для заданных значений определяются постоянных . В краевой задаче на искомую функцию и ее производные накладываются краевых условий в точках и интервала .

Пример. Найти частное решение уравнения , удовлетворяющее при 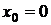начальным условиям .

◄ Общее решение данного простейшего уравнения получено выше:

;

;

.

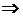
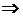
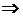
Подставляя полученные значения постоянных интегрирования в общее решение, получаем искомое частное решение уравнения

. ►

График каждого частного решения называется интегральной кривой; совокупность всех таких графиков образует семейство интегральных кривых, зависящее от параметров ( –параметрическое семейство).

Пример. Функция является общим решением уравнения , что можно проверить ее подстановкой в это уравнение. Совокупность графиков этой функции при различных значениях постоянной интегрирования 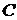образует семейство равносторонних гипербол, асимптотами которых являются оси координат (рис. 5.1).

Рис. 5.1

Частное решение , соответствующее начальному условию , задает гиперболу, проходящую через точку . ►