Линейные векторные пространства. Определяющие свойства

Пусть 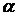, , 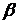… есть действительные числа (принадлежат множеству (полю) действительных чисел 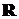). Будем называть их скалярами. В качестве скаляров могут выступать и комплексные числа (будут рассматриваться позже). Множество 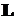объектов (элементов) 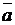, , 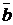, 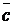…называется линейным векторным пространством (действительным или комплексным в зависимости от того, действительные или комплексные числа рассматриваются), а элементы 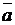, , 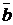, 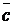…называются векторами, если определены две бинарные операции ― векторное сложение и умножение вектора на скаляр такие, что

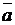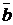
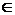
1) для каждой пары элементов , 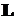пространство 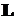содержит их векторную сумму 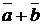и

,

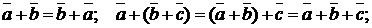
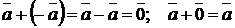где 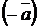– элемент (вектор), противоположный (аддитивно обратный) элементу (вектору) 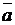, – нуль или нулевой элемент (вектор);

2) 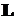содержит произведение 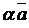каждого элемента (вектора) 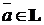на любой скаляр 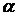, причем

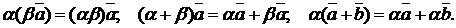
Подчеркнем, что элементами линейного векторного пространства могут быть не только вектора в привычном понимании, но, как будет видно далее, и другие математические объекты (например, некоторые типы матриц, функций). Эти объекты также будут условно считаться векторами.

Будем рассматривать пока только действительные векторные пространства.

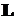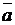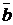Векторное пространство называется унитарным векторным пространством, если в нем определена бинарная операция, ставящая каждой паре векторов и из 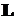в соответствие скаляр (действительное число) 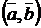– скалярное, или внутреннее, произведение 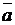и 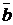, причем:

1) 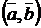= 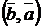(коммутативный закон);

2) 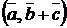= 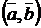+ 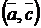(дистрибутивный закон);

3) 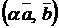= = 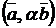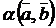(ассоциативный закон);

4) 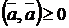для любого вектора 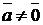; 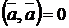при 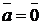(положительная определенность).

Не трудно убедиться, что введенное ранее определение скалярного произведения для векторов в привычном понимании удовлетворяет этому общему определению скалярного произведения для унитарных векторных пространств.

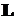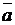
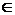
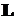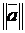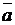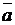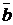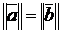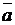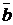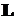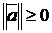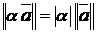Векторное пространство называется нормированным векторным пространством, если для каждого вектора существует такое действительное число (норма, абсолютная величина, модуль вектора ), что из = следует и что для всех и из :

, , из 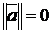следует, что 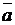=0,

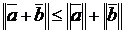(неравенство Минковского). (1.2.14)

Каждое унитарное векторное пространство позволяет формулами

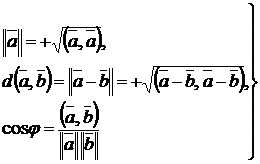(1.2.15)

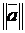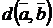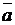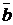ввести норму (абсолютную величину, модуль) каждого вектора, расстояние (метрику) между двумя «точками» и из 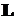и угол 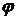между любыми двумя векторам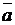и и .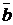

Таким образом, любое нормированное векторное пространство является и метрическим пространством, т. к. допускает метрику как обобщенное понятие расстояния между любыми двумя элементами абстрактного множества.

Норма 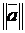обобщает обычное понятие о длине вектора, а неравенство Минковского (1.2.14) – известный факт, что в обычном треугольнике длина любой из его сторон не превосходит суммы длин двух других сторон (отсюда другое название этого неравенства – «неравенство треугольника»).