Построение моделей в условиях мультиколлинеарности независимых переменных.

Имеются данные о заработной плате у (тысяч рублей), возрасте х₁ (лет), стаже работы по специальности х₂ (лет) и выработке х₃ (штук в смену) по 15 рабочим цеха:

№	y	х1	х2	х3
	3,2
	4,5
	3,3
	3,0
	2,8
	3,9
	3,7
	4,2
	4,7
	4,4
	2,9
	3,7
	2,4
	4,5
	2,6

Требуется:

1. С помощью определителя матрицы парных коэффициентов межфакторной корреляции оценить мультиколлинеарность факторов,
исключить из модели фактор, ответственный за мультиколлинеарность.

2. Построить уравнение множественной регрессии в стандартизованной
форме:

2.1. Оценить параметры уравнения.

2.2. Используя стандартизованные коэффициенты регрессии
сравнить факторы по силе их воздействия на результат.

2.3. Оценить тесноту связи между результатом и факторами с помощью коэффициента множественной корреляции.

2.4. Оценить с помощью коэффициента множественной
детерминации качество модели.

2.5. Используя F-критерий Фишера оценить статистическую
значимость присутствия каждого из факторов в уравнении регрессии.

3. Построить уравнение множественной регрессии в естественной форме, пояснить экономический смысл параметров уравнения.

4. Найти среднюю ошибку аппроксимации.

5. Рассчитать прогнозное значение результата, если прогнозное значение факторов составит: х₁ = 35 лет, х₂ = 10 лет, х₃ = 20 штук в смену.

Решение.

Для оценки мультиколлинеарности факторов используем определитель матрицы парных коэффициентов корреляции между факторами.

Определим парные коэффициенты корреляции.

Для этого рассчитаем таблицу 7.

Используя рассчитанную таблицу, определяем дисперсию y, x₁, x₂, x₃.

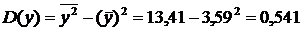
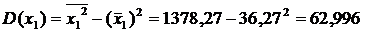
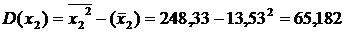
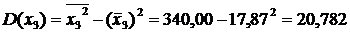
Найдем среднее квадратическое отклонение признаков y, x₁, x₂, x₃, как корень квадратный из соответствующей дисперсии.

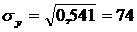
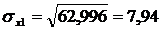
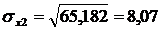
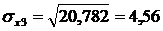
Определим парные коэффициенты корреляции:

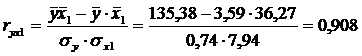
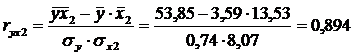
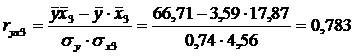
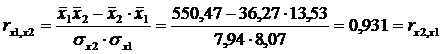
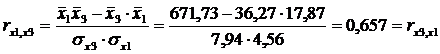
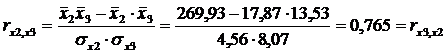
таблица 7

№	y	y2	x1	x12	x2	x22	x3	x32	yx1	yx2	yx3	x1x2	x1x3	x2x3		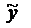	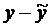Аi
	3,2	10,24							96,0	19,2	38,4				2,87	0,33	10,18
	4,5	20,25							184,5	81,0	90,0				4,00	0,50	11,03
	3,3	10,89							122,1	36,3	39,6				3,32	-0,02	0,73
	3,0	9,00							99,0	27,0	54,0				3,38	-0,38	12,79
	2,8	7,84							67,2	11,2	42,0				2,65	0,15	5,47
	3,9	15,21							171,6	74,1	66,3				4,04	-0,14	3,54
	3,7	13,69							136,9	66,6	62,9				3,59	0,11	3,03
	4,2	17,64							163,8	92,4	109,2				4,19	0,01	0,20
	4,7	22,09							230,3	141,0	122,2				4,83	-0,13	2,86
	4,4	19,36							211,2	105,6	96,8				4,56	-0,16	3,61
	2,9	8,41							84,1	23,2	52,2				3,13	-0,23	7,82
	3,7	13,69							114,7	22,2	74,0				3,36	0,34	9,17
	2,4	5,76							62,4	12,0	24,0				2,51	-0,11	4,65
	4,5	20,25							211,5	85,5	90,0				4,39	0,11	2,46
	2,6	6,76							75,4	10,4	39,0				2,97	-0,37	14,17
σ	53,8	201,08							2030,7	807,7	1000,6				53,80	0,00	91,69
ср.	3,59	13,41	36,27	1378,27	13,53	248,33	17,87	340,00	135,38	53,85	66,71	550,47	671,73	269,93	3,59	0,00	6,11

Матрица парных коэффициентов корреляции:

	y	x1	x2	x3
y	1,000
x1	0,908	1,000
x2	0,894	0,931	1,000
x3	0,783	0,657	0,765	1,000

Анализируем матрицу парных коэффициентов корреляции.

ú r_x1x2=0.931, т. е. между факторами x₁ и x₂ существует сильная корреляционная связь, один из этих факторов необходимо исключить.

ú r_x1x3=0.657 меньше, чем r_x2x3=0.765, т.е. корреляция фактора х₂ с фактором х₃ сильнее, чем корреляция факторов х₁ и х₃.

ú Из модели следует исключить фактор х₂, т.к. он имеет наибольшую тесноту связи с х₃ и, к тому же, менее тесно (по сравнению с x₁) связан с результатом у (0.894<0.908).

2.1. Уравнение регрессии в естественной форме будет иметь вид:

y_x = a + b_lx_]+b₃x₃,

фактор х₂ исключен из модели.

Стандартизованное уравнение:

t_y = β₁t_x1+β₃t_x3

где: t_y , t_x1, t_x3 – стандартизованные переменные.

Параметры уравнения β₁ и β₃ определим методом наименьших квадратов из системы уравнений:

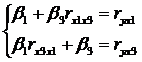
Или:

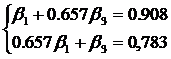
Систему решаем методом Крамера:

∆=		0,657	= 1-0,6572= 0,568
0,657

∆β1=	0,908	0,657	= 0,908-0,657–0,783=0,394
0,783

∆β3=		0,571	=0,833-0,571–0,413= 0,186
0,413	0,833

Тогда:

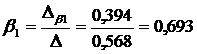
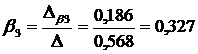
Получили уравнение множественной регрессии в стандартизованном масштабе:

t_y = 0,693t_x1+0,327t_x3

Коэффициенты β₁ и β₃ сравнимы между собой в отличии от коэффициентов чистой регрессии b₁ и b₃.

β₁=0,693 больше β₃=0,327, следовательно, фактор x₁ сильнее влияет на результат y чем фактор x₃.

Определим индекс множественной корреляции:

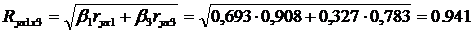
Cвязь между y и факторами x₁, x₃ характеризуется как тесная, т. к. значение индекса множественной корреляции близко к 1.

Коэффициент множественной детерминации:

R ²_yx1x3=(0.941)²=0.886

Т. е. данная модель объясняет 88,6% вариации y, на долю неучтенных в модели факторов приходится 100-88,6=11,4%

Оценим значимость полученного уравнения регрессии с помощью F-критерия Фишера:

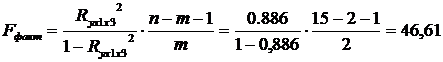
F_табл(α=0,05; k₁=2; k₂=15-2-1=12)=3,88

Табличное значение критерия Фишера (определяем по таблице значений критерия Фишера при заданном уровне значимости α и числе степеней свободы k₁ и k₂) меньше фактического значения критерия. следовательно, гипотезу H₀ о том, что полученное уравнение статистически незначимо и ненадежно, отвергаем и принимаем альтернативную гипотезу H₁: полученное уравнение статистически значимо, надежно и пригодно для анализа и прогноза.

Оценим статистическую значимость включения в модель факторов x₁ и x_2.

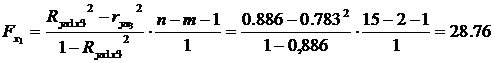
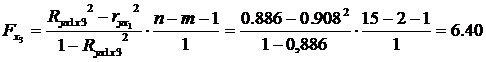
F_табл (α=0,05; k₁=1; k₂=15-2-1=12)=4,75

F_x1 >F_табл.

F_x3 >F_табл.

Значит, включение в модель факторов x₁ и x₃ статистически значимо.

Перейдем к уравнению регрессии в естественном масштабе:

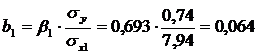
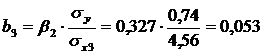
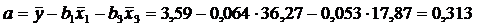
Уравнение множественной регрессии в естественном масштабе:

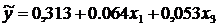
Экономическая интерпретация параметров уравнения:

b₁=0.064, это значит, что с увеличением x₁ – возраста рабочего на 1 год заработная плата рабочего увеличивается в среднем на 64 рубля, если при этом фактор x₂ - выработка рабочего не меняется и фиксирован на среднем уровне.

b₃=0,053, это значит, что с увеличением x₃ – выработки рабочего на 1 шт. в смену, заработная плата рабочего увеличивается в среднем на 53 рубля, если при этом фактор x₁ - возраст рабочего не меняется и фиксирован на среднем уровне.

a=0,313 не имеет экономической интерпретации, формально это значение результата y при нулевом значении факторов, но факторы могут и не иметь нулевого значения.

Найдем величину средней ошибки аппроксимации, таблица 7.

Ошибка аппроксимации А_i, i=1…15:

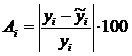
Средняя ошибка аппроксимации:

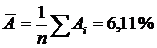
Ошибка небольшая, качество модели высокое.

Используем полученную модель для прогноза.

Если х₁ =35, х₂ =10, х₃ =20, то

у_р = 0,313 + 0,064•35 + 0,053•20 = 3,618 тыс. руб.

Вывод. Для рабочего данного цеха, возраст которого 35 лет, а выработка 20 шт. в смену, прогнозное значение заработной платы - 3618 руб.

Варианты заданий.

Вариант № 1

	48,72	53,01	51,39	73,71	67,16	69,27	42,09

Вариант № 2

	46,22	51,11	49,09	71,51	64,46	66,67	39,99

Вариант № 3

	47,22	50,41	49,39	70,61	65,16	67,07	40,59

Вариант № 4

	45,92	48,81	47,59	67,91	62,56	64,47	39,69

Вариант № 5

	47,62	49,41	48,79	68,01	63,76	65,47	41,39

Вариант № 6

	36,52	36,61	36,19	52,51	49,56	51,07	31,09

Вариант № 7

	35,42	33,71	34,09	48,31	47,06	48,27	30,19

Вариант № 8

	35,42	34,61	35,59	52,51	50,96	52,17	28,99

Вариант № 9

	40,32	41,91	42,49	63,31	59,86	61,37	32,89

Вариант № 10

	49,52	52,21	52,19	74,11	69,56	71,27	42,09

Вариант № 11

	36,22	38,01	37,79	56,61	52,36	54,07	29,99

Вариант № 12

	52,12	51,91	51,29	79,51	66,26	67,97	43,89

Вариант № 13

	37,52	35,91	35,69	49,11	47,46	48,77	32,89

Вариант № 14

	49,92	51,81	50,59	69,01	64,36	66,17	44,29

Вариант № 15

	49,92	50,91	51,09	70,11	66,86	68,37	43,29

Вариант № 16

	40,72	40,81	40,39	56,71	53,76	55,27	35,29

Вариант № 17

	42,92	46,51	45,09	66,41	60,46	62,47	36,49

Вариант № 18

	58,02	62,61	61,19	84,41	77,76	79,87	50,99

Вариант № 19

	44,72	46,61	45,39	63,81	59,16	60,97	39,09

Вариант № 20

	37,92	39,21	39,59	59,51	56,16	57,67	30,89

Вариант № 21

	42,82	43,81	43,99	63,01	59,76	61,27	36,19

Вариант № 22

	47,12	49,21	48,79	68,91	64,56	66,27	40,49

Вариант № 23

	51,12	50,71	51,29	68,31	66,26	67,57	44,89

Вариант № 24

	53,12	57,01	55,79	78,01	71,96	73,97	46,29

Вариант № 25

	43,12	45,71	44,29	63,71	58,46	60,37	37,29

Вариант № 26

	53,12	56,61	55,79	77,91	72,36	74,27	46,09

Вариант № 27

	49,52	51,21	51,19	71,21	67,36	68,97	42,69

Вариант № 28

	43,72	48,01	46,39	68,71	62,16	64,27	37,09

Вариант № 29

	47,22	5,51	48,89	69,31	63,46	65,47	41,19

Вариант № 30

	36,92	39,41	38,59	58,81	53,96	55,77	30,49

Задание 3- 4. Моделирование динамики развития экономических систем

Цель лабораторной работы: приобретение практических навыков разработки и исследования математических моделей динамики развития экономических систем.