Вычисление ранга матрицы. Нахождение линейной

Зависимости между векторами

Докажем вначале следующую теорему:

Теорема 2.1 (Стейница). Если в жордановой таблице все строки линейно независимы и их количество не превосходит количества столбцов (m £ n), то в результате m последовательных шагов жордановых исключений можно переместить наверх все y_j (j = 1, 2,…, m).

Доказательство. Помешать переброске наверх переменной y_j может невозможность выбора разрешающего элемента, то есть равенство нулю соответствующих элементов j-ой строки. Предположим, что после k шагов метода жордановых исключений (k < m) мы пришли к следующей таблице:

	y1	y2	…	yk	xk+1	…	xn
x1	b11	b12	…	b1k	b1, k+1	…	b1n
x2	b21	b22	…	b2k	b2, k+1	…	b2n
…	……………………………………….	…………………………….
xk	bk1	bk2	…	bkk	bk, k+1	…	bkn
yk+1	bk+1, 1	bk+1, 2	…	bk+1, k		…
yk+2	bk+2, 1	bk+2, 2	…	bk+2, k		…
…	……………………………………….	…………………………….
ym	bm1	bm2	…	bmk		…

Табл. 2.1.

Если переменные y_k+1, y_k+2,…, y_m дальше перебрасывать наверх нельзя, то это означает, что соответствующие разрешающие элементы, расположенные в правом нижнем углу таблицы, равны нулю. Но в этом случае переменные y_k+1, y_k+2,…, y_m линейно выражаются через
y₁, y₂,…, y_k. Действительно:

y_k+1 = b_{k+1, 1} ´ y₁+ b_{k+1, 2} ´ y₂ +…+ b_{k+1, k} ´ y_k,

y_k+2 = b_{k+2, 1} ´ y₁+ b_{k+2, 2} ´ y₂ +…+ b_{k+2, k} ´ y_k,

……………………………………………….

y_m = b_m1 ´ y₁ + b_m2 ´ y₂ +…+ b_mk ´ y_k.

Полученное противоречие доказывает то, что все игреки можно перенести наверх, что и требовалось доказать. Рассмотрим два примера.

Пример 2.1. Вычислить ранг матрицы .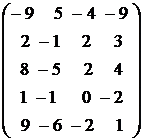

Решение. Составим для этой матрицы жорданову таблицу (таблица 2.2). Будем переносить переменные x_i наверх, пока это возможно. По теореме Стейница в верхнюю часть таблицы можно переместить столько переменных из левого заглавного столбца, сколько в таблице линейно независимых строк. А это и есть ранг матрицы.

	y1	y2	y3	y4			y1	x2	y3	y4
x1	–9		–4	–9		x1		–5
x2		–1				y2		–1
x3		–5				x3	–2		–8	–11
x4		–1		–2		x4	–1		–2	–5
x5		–6	–2			x5	–3		–14	–17

Табл. 2.2. Табл. 2.3.

При переходе от таблицы 2.2 к таблице 2.3 в качестве разрешающей строки и разрешающего столбца выбраны вторая строка и второй столбец (разрешающий элемент a₂₂ = –1) и так далее. После трех шагов метода обыкновенных жордановых исключений мы придем к таблице 2.5:

	x1	x2	y3	y4			x1	x2	x3	y4
y1			–6	–6		y1	–2	–2,5	–1,5	–4,5
y2			–10	–9		y2	–3	–3,5	–2,5	–6,5
x3	–2	–5				y3	0,5	1,25	0,25	–0,25
x4	–1	–4				x4
x5	-3	-9				x5	-1	-4

Табл. 2.4. Табл. 2.5.

Дальнейший перевод переменных наверх невозможен из-за равенства нулю соответствующих разрешающих элементов (b₄₄ = b₅₄ = 0). Следовательно, по теореме Стейница ранг матрицы равен трем. Заметим, что кроме ранга матрицы мы попутно нашли зависимость между ее строками. Действительно, из последних двух строк таблицы 2.5 получим:

x₄ = 1 ´ x₁+ 1 ´ x₂ + 1´ x₃ = x₁ + x₂ + x₃,

x₅ = – 1 ´ x₁ – 4 ´ x₂ + 1´ x₃ = – x₁ – 4x₂ + x₃.

Из последних равенств вытекает то, что четвертая строка исходной матрицы равна сумме первых трех строк, а пятая строка равна третьей строке минус первая строка и минус вторая строка, умноженная на четыре.

Пример 2.2. Проверить, являются ли векторы a₁ = (6; 8; – 2; – 1),
a₂ = (4; 2; – 2; 1), a₃ = (1; 3; 0; – 1) и a₄ = (– 7; – 1; 4; – 3) – линейно независимыми. В случае отрицательного ответа, указать соответствующую зависимость.

Решение. Линейная зависимость между векторами эквивалентна линейной зависимости между строками матрицы 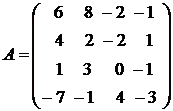, составленной из координат этих векторов. Таким образом, данная задача решается аналогично задаче о нахождении ранга матрицы. Составим исходную жорданову таблицу 2.6 и сделаем два шага методом обыкновенных жордановых исключений, выбрав в качестве разрешающих элементов соответственно a₃₁ = 1 и b₂₃ = – 2. В результате приходим к таблице 2.8:

	y1	y2	y3	y4			x3	y2	y3	y4
x1			–2	–1		x1		–10	–2
x2			–2			x2		–10	–2
x3				–1		y1		–3
x4	–7	–1		–3		x4	–7			–10

Табл. 2.6. Табл. 2.7.

	x3	y2	x2	y4
x1
y3		–5	–0,5	2,5
y1		–3
x4			–2

Табл. 2.8.

Дальнейший перевод иксов наверх невозможен из-за равенства нулю соответствующих разрешающих элементов. Следовательно, векторы
a₁, a₂, a₃, a₄, являются линейно зависимыми. Причем a₁ = 2a₃ + a₂,
a₄ = a₃ – 2a₂. Последние соотношения видны из первой и четвертой строки таблицы 2.8.