Примитивно вычислимые функции
Базисными функциями называются следующие функции: 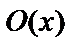 – нулевая функция;
– нулевая функция; 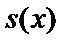 – функция следования;
– функция следования; 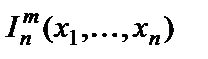
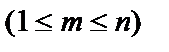 – функция выбора.
– функция выбора.
Оператор суперпозиции (подстановки) 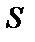 ставит в соответствие
ставит в соответствие 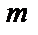 –местной операции
–местной операции 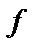 и
и 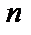 – местным операциям
– местным операциям 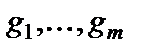
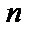 –местную операцию
–местную операцию 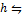
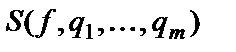 , удовлетворяющую тождеству:
, удовлетворяющую тождеству:
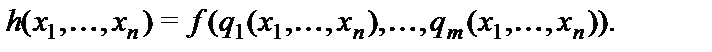
Оператор примитивной рекурсии 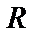 ставит в соответствие
ставит в соответствие 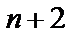 – местной операции
– местной операции 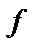 и
и 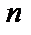 – местной операции
– местной операции 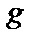
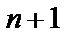 – местную операцию
– местную операцию 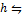
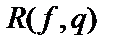 , удовлетворяющую схеме примитивной рекурсии:
, удовлетворяющую схеме примитивной рекурсии:
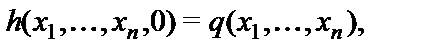
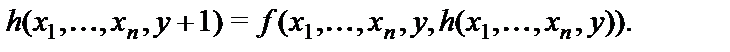

Функция 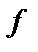 называется примитивно рекурсивной (ПРФ), если существует последовательность функций
называется примитивно рекурсивной (ПРФ), если существует последовательность функций 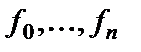 , в которой
, в которой 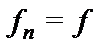 и всякая
и всякая 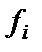 является либо базисной функцией, либо получается из предыдущих функций с помощью оператора суперпозиции
является либо базисной функцией, либо получается из предыдущих функций с помощью оператора суперпозиции 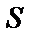 или примитивной рекурсии
или примитивной рекурсии 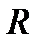 .
.
Пример 1.Функция сложения 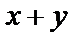 является ПРФ:
является ПРФ:
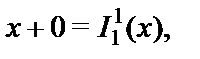
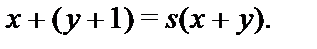
Пример 2.Функция умножения 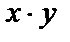 является ПРФ:
является ПРФ:
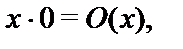
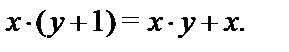

Частично рекурсивные функции
Оператор минимизации 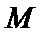 ставит в соответствие
ставит в соответствие 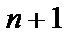 – местной операции
– местной операции 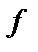
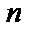 –местную операцию
–местную операцию 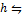
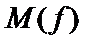 так, что
так, что
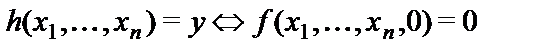
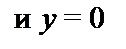
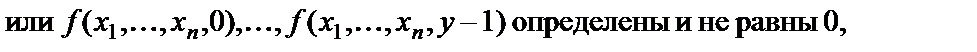
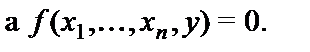
В этом случае введем обозначение: 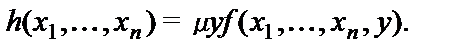
Функция 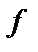 называется частично рекурсивной (ЧРФ), если существует последовательность функций
называется частично рекурсивной (ЧРФ), если существует последовательность функций 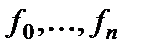 , в которой
, в которой 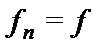 и всякая
и всякая 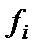 является либо базисной функцией, либо получается из предыдущих функций с помощью оператора суперпозиции
является либо базисной функцией, либо получается из предыдущих функций с помощью оператора суперпозиции 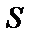 , примитивной рекурсии
, примитивной рекурсии 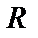 или минимизации
или минимизации 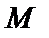 .
.
Пример 1.Нигде не определенная функция 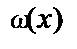 является ЧРФ:
является ЧРФ:
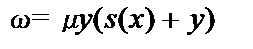 .
.
Пример 2.Функция
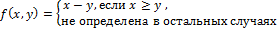
является ЧРФ:
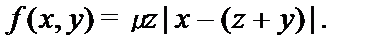
ЗАДАНИЯ ДЛЯ домашних И КОНТРОЛЬНЫХ РАБОТ
Совершенные дизъюнктивные нормальные формы, совершенные конъюнктивные нормальные формы
Построить таблицы истинности для следующих формул алгебры высказываний и привести эти формулы к СДНФи СКНФ.
| 1. (x∧y)→(y∧z); |
| 2. (x→y)→(y∧z); |
| 3. ((x∧y)→x)→z; |
| 4. (x∧(y→z)→x∨(y∧z); |
| 5. z→(x∧y)∨(y∧z); |
| 6. ((x∨z)∧y)→(y→z); |
| 7. (x∧(z→y)→y)∨z); |
| 8. ((x∧y)→z∨(y∧z); |
| 9. (((x→y)→z)∨y)∧z; |
| 10) x∧(z→y)→z∨y; 11) ((x∨z)∧y)→(y→z); |
| 12) (x→y)→z∨(y∧z); |
| 13) x→(y→z)∧(z∨x); |
| 14) ((x∧z)→y)∨z; |
| 15) ((x→y)∧z→z)∨y; |
| 16) x∨(z→y)→(y∧z); |
| 17) ((x∧z→y)→z)∨z; |
| 18) (x∧z →y)→z∨y; |
| 19) (x→y∧z)∨y→z; |
| 20) x→(y→z)∨(y∧z); |
| 21) ((x∨y)→z)→(y∧z); |
| 22) (x→y)→(z∨y)∧z; |
| 23) ((x→y)∧z)∨y)→z; |
| 24) (z→y)→x∧(z∨y)∧z; |
| 25) ((x∧z)∨y)→z∧(x→y). |
Логическое следствие в алгебре высказываний
Проверить истинность соотношений тремя способами(используя определение логического следствия и пп. 3,4 теоремы 2.
1. 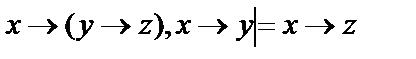 ;
;
2. 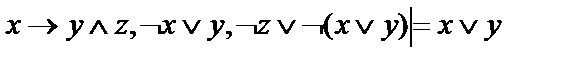 ;
;
3. 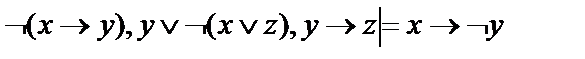 ;
;
4. 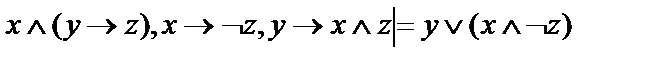 ;
;
5. 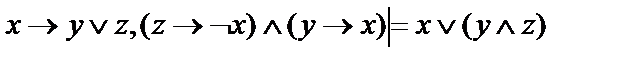 ;
;
6. 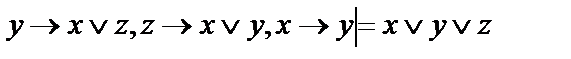 ;
;
7. 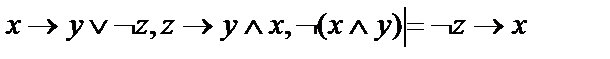 ;
;
8. 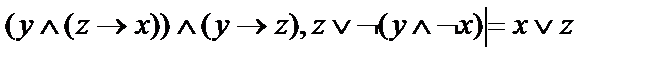 ;
;
9. 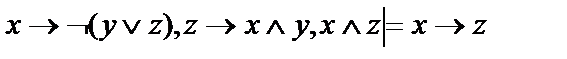 ;
;
10. 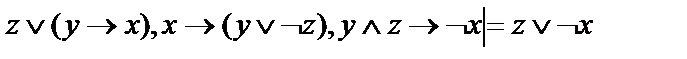 ;
;
11. 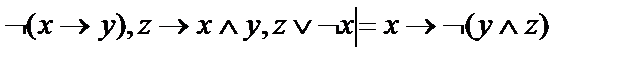 ;
;
12. 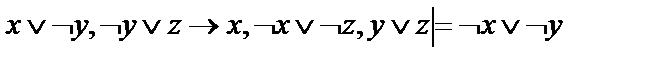 ;
;
13. 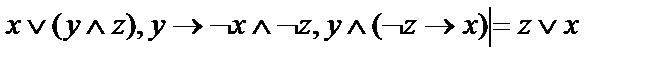 ;
;
14. 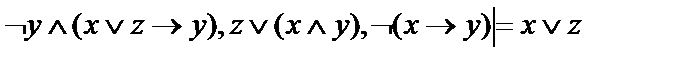 ;
;
15. 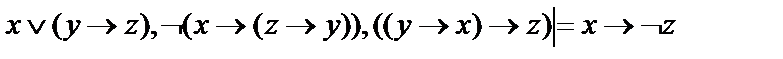 ;
;
16. 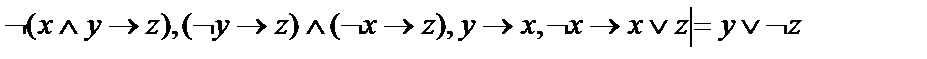 ;
;
17. 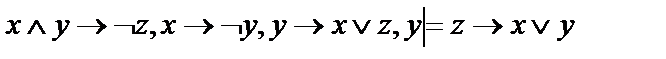 ;
;
18. 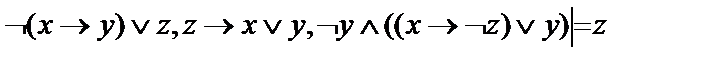 ;
;
19. 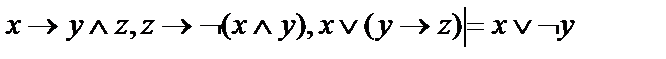 ;
;
20. 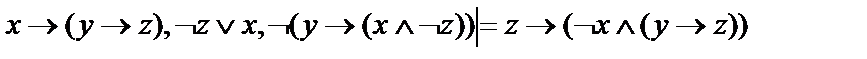 ;
;
21. 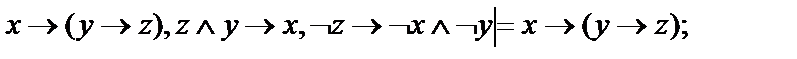
22. 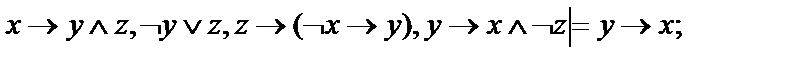
23. 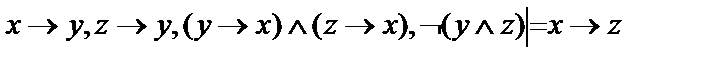 ;
;
24. 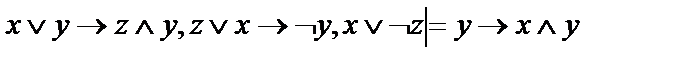 ;
;
25. 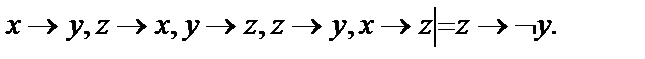
Исчисление высказываний
Пусть 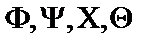 - формулы исчисления высказываний. Построить вывод формулы исчисления высказываний из данного множества гипотез.
- формулы исчисления высказываний. Построить вывод формулы исчисления высказываний из данного множества гипотез. 

1. 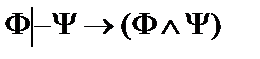 ;
;
2. 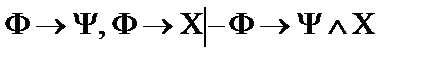 ;
;
3. 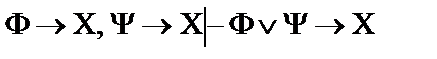 ;
;
4. 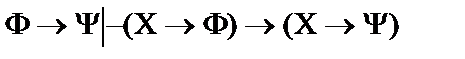 ;
;
5. 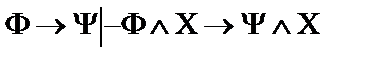 ;
;
6. 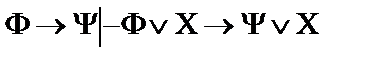 ;
;
7. 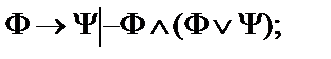
8. 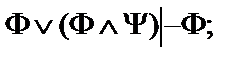
9. 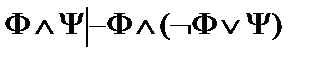 ;
;
10. 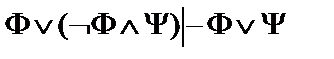 ;
;
11. 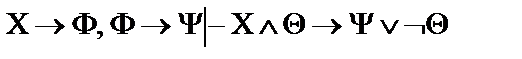 ;
;
12. 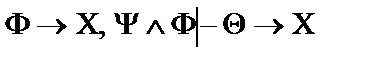 ;
;
13. 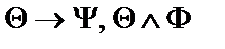
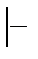
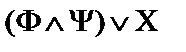 ;
;
14. 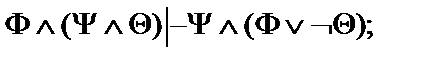
15. 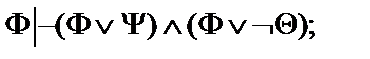
16. 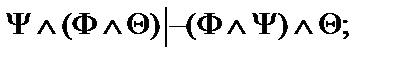
17. 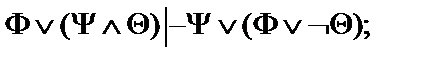
18. 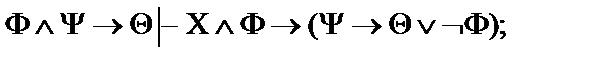
19. 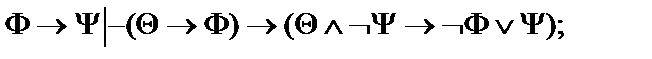
20. 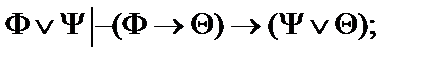
21. 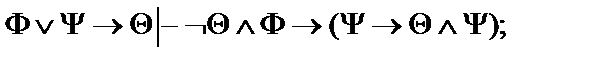
22. 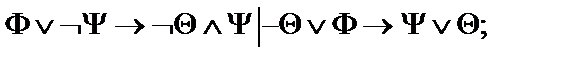
23. 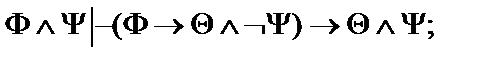
24. 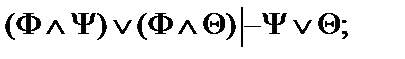
25. 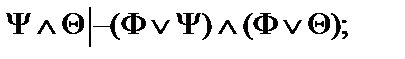
26. 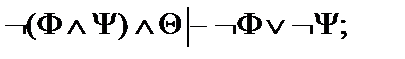
27. 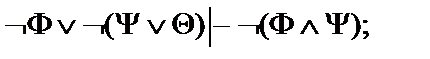
28. 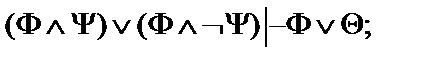
29. 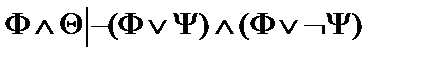
Логика предикатов. Алгебраические системы.
Построить подсистемуалгебраической системы 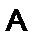 , порожденную множеством
, порожденную множеством 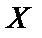 (через
(через 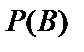 обозначен булеан множества B,т.е. множество всех подмножеств множества B):
обозначен булеан множества B,т.е. множество всех подмножеств множества B):
1. 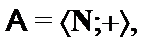
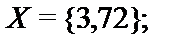
2. 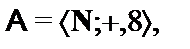
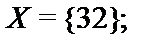
3. 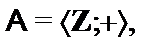
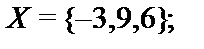
4. 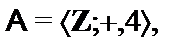
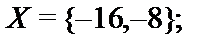
5. 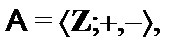
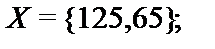
6. 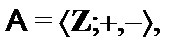
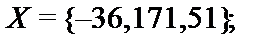
7. 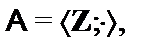
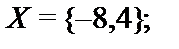
8. 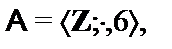
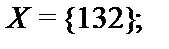
9. 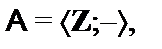
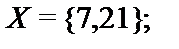
10. 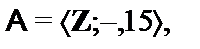
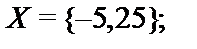
11. 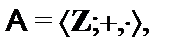
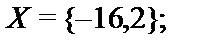
12. 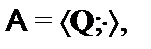
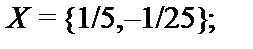
13. 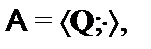
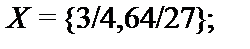
14. 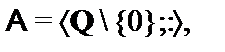
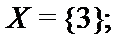
15. 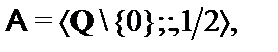
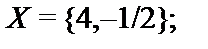
16. 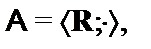
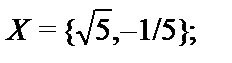
17. 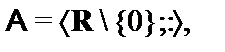
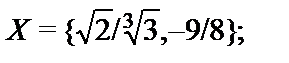
18. 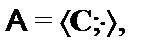
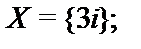
19. 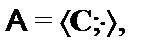
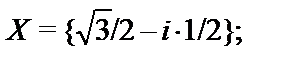
20. 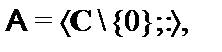
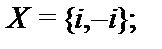
21. 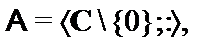
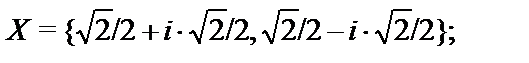
22. 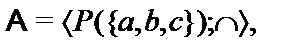
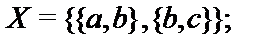
23. 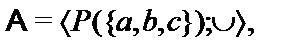
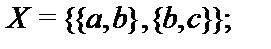
24. 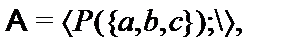
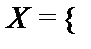 Ø,
Ø, 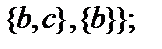
25. 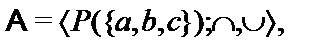
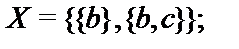
26. 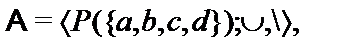
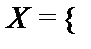 Ø,
Ø, 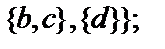
27. 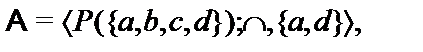
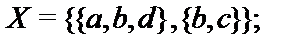
28. 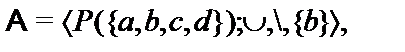
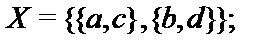
29. 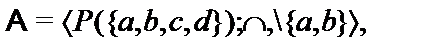
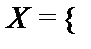 Ø,
Ø, 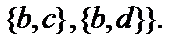
Формулы ЛП
Выписать все подформулы данной формулы сигнатуры 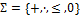 иопределить свободные и связанные переменные формулы:
иопределить свободные и связанные переменные формулы:
1. 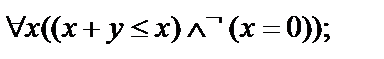
2. 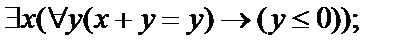
3. 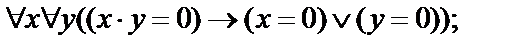
4. 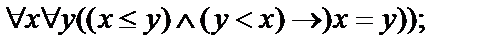
5. 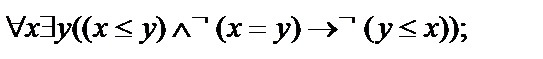
6. 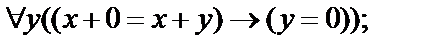
7. 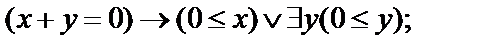
8. 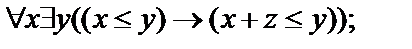
9. 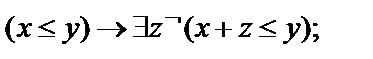
10. 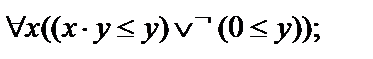
11. 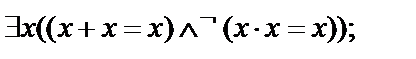
12. 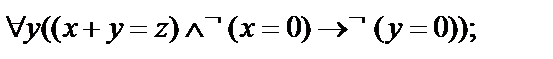
13. 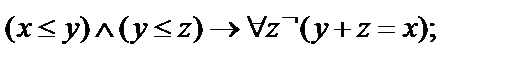
14. 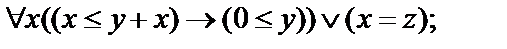
15. 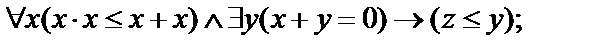
16. 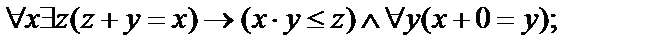
17. 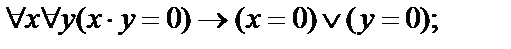
18. 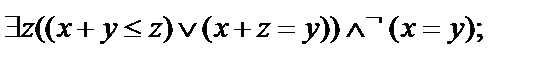
19. 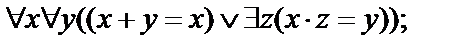
20. 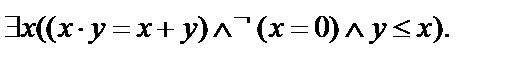
Пусть 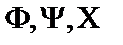 - атомарные формулы логики предикатов.Выписать все подформулы данной формулы и определить свободные и связанные переменные формулы:
- атомарные формулы логики предикатов.Выписать все подформулы данной формулы и определить свободные и связанные переменные формулы:
1. 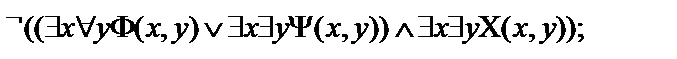
2. 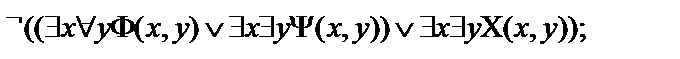
3. 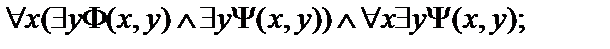
4. 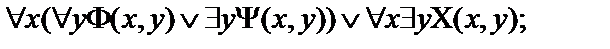
5. 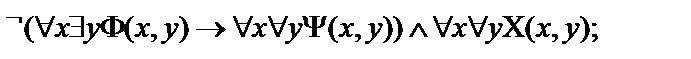
6. 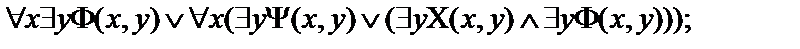
7. 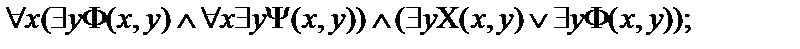
8. 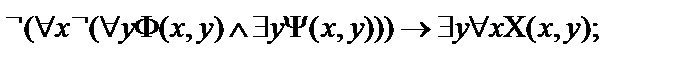
9. 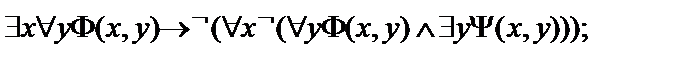
10. 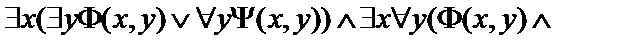
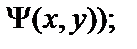
11. 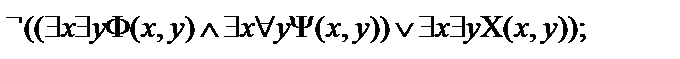
12. 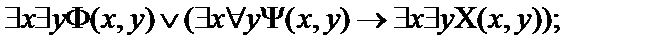
13. 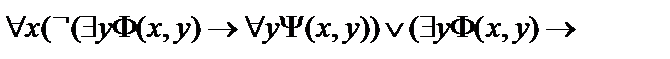
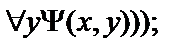
14. 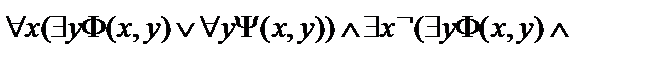
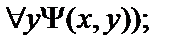
15. 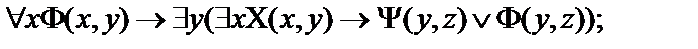 ,
,
16. 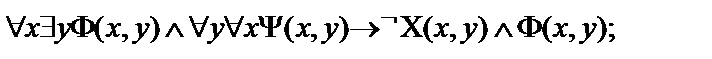
17. 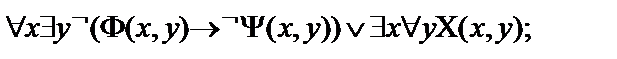
18. 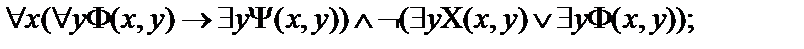
19. 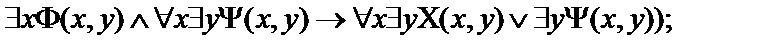
20. 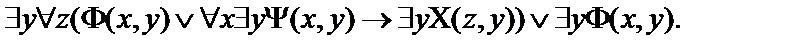
Истинность формулыЛП
В алгебраической системе
Написать формулу Ф(х), истинную в алгебраической системе 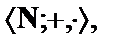 тогда и только тогда, когда
тогда и только тогда, когда
1. х=1;
2. х=2nдля некоторого натуральногоn;
3. х>4;
4. х – нечетное число;
5. х – простое число.
Написать формулу Ф(х,y), истинную в алгебраической системе 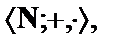 тогда и только тогда, когда
тогда и только тогда, когда
1. 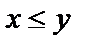 ;
;
2. 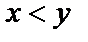 ;
;
3. х делит 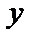 ;
;
4. 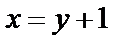 ;
;
5. 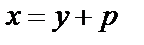 , где p - простое число.
, где p - простое число.
Написать формулу Ф(х,y,z), истинную в алгебраической системе 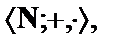 тогда и только тогда, когда
тогда и только тогда, когда
1. xделится на yс остатком 2;
2. x+3y>2z;
3. z – общий делитель yи z;
4. z = НОК (x,y);
5. z = НОД (x,y).
Написать формулу Ф(х,y,z), истинную в алгебраической системе 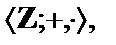 тогда и только тогда, когда
тогда и только тогда, когда
1. x=0;
2. x=-1;
3. 2x-3y – четное число;
4. 3z=4x-5y;
5. z-2yделится на3x.
Пусть 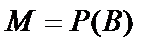 – булеан множества B,т.е. множество всех подмножеств множества B.Написать формулу Ф(х,y,z), истинную в алгебраической системе
– булеан множества B,т.е. множество всех подмножеств множества B.Написать формулу Ф(х,y,z), истинную в алгебраической системе 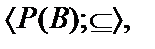 тогда и только тогда, когда
тогда и только тогда, когда
1. 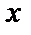 есть пересечение
есть пересечение 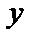 и
и 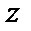 ;
;
2. 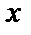 есть объединение
есть объединение 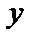 и
и 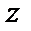 ;
;
3. 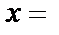 Ø;
Ø;
4. 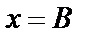 ;
;
5. 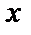 есть дополнение
есть дополнение 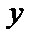 .
.
Пусть 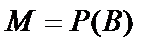 – булеан множества B,т.е. множество всех подмножеств множества B.Написать формулу Ф(х,y,z), истинную в алгебраической системе
– булеан множества B,т.е. множество всех подмножеств множества B.Написать формулу Ф(х,y,z), истинную в алгебраической системе 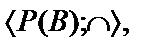 тогда и только тогда, когда
тогда и только тогда, когда
1. 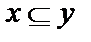 ;
;
2. 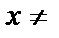 Ø;
Ø;
3. 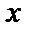 есть одноэлементное множество;
есть одноэлементное множество;
4. 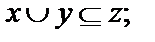
5. 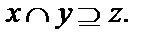
Написать формулу 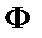 , такую что
, такую что
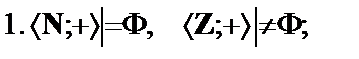
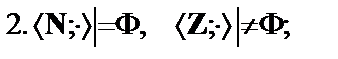
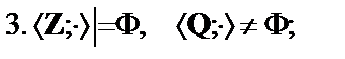
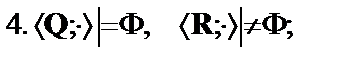
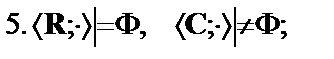
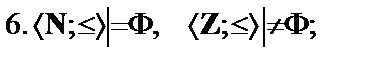
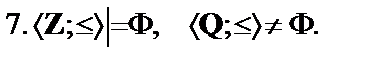
Логическое следствие в ЛП
Пусть 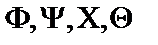 – формулы логики предикатов,
– формулы логики предикатов, 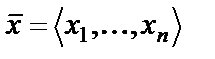 и .
и . 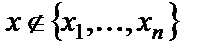 .Доказать следующие соотношения.
.Доказать следующие соотношения.
1. 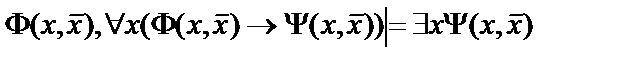 ;
;
2. 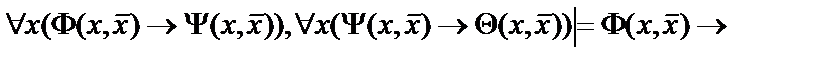
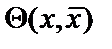 ;
;
3. 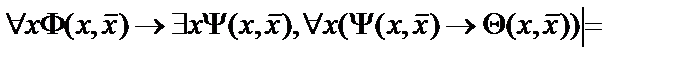
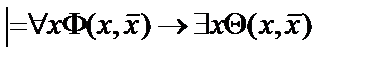 ;
;
4. 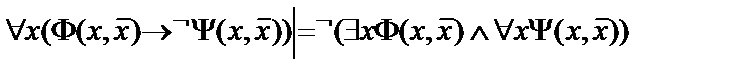 ;
;
5. 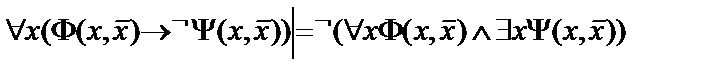 ;
;
6. 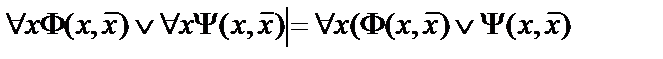 ;
;
7. 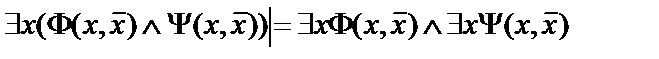 ;
;
8. 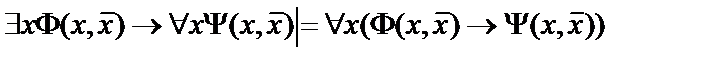 ;
;
9. 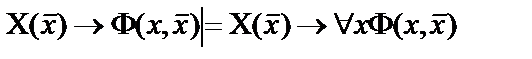 ;
;
10. 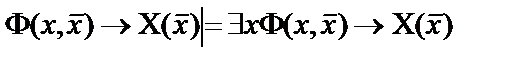 ;
;
11. 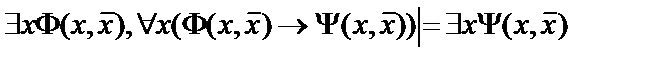 ;
;
12. 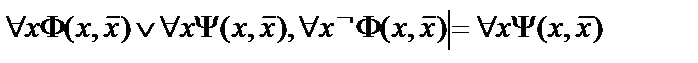 ;
;
13. 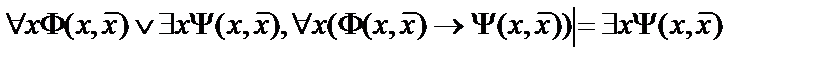 ;
;
14. 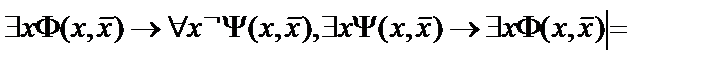
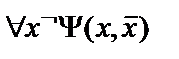 ;
;
15. 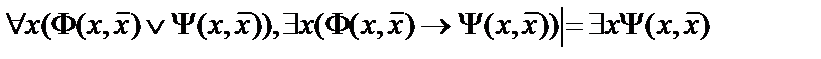 ;
;
16. 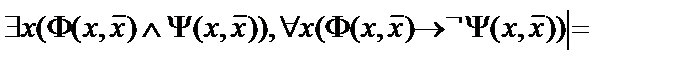
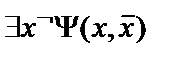 ;
;
17. 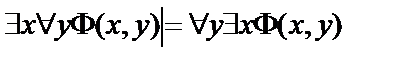 .
.
Пусть 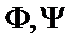 – формулы логики предикатов.Проверить следующие соотношения.
– формулы логики предикатов.Проверить следующие соотношения.
1. 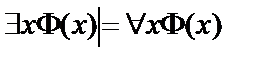 ;
;
2. 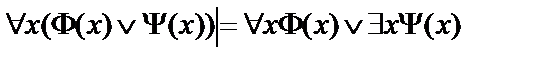 ;
;
3. 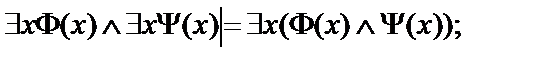
4. 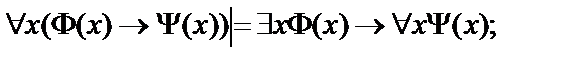
5. 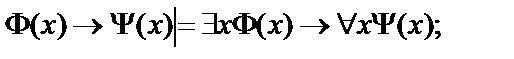
6. 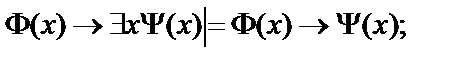
7. 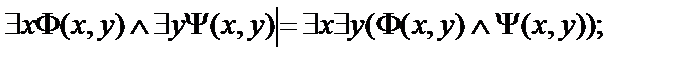
8. 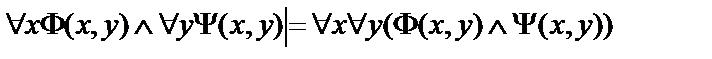
9. 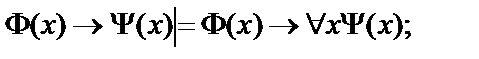
10. 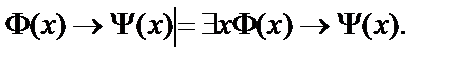
Исчисление предикатов
Пусть 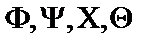 - формулы исчисления предикатов. Построить вывод формулы исчисления предикатов из данного множества гипотез.
- формулы исчисления предикатов. Построить вывод формулы исчисления предикатов из данного множества гипотез. 

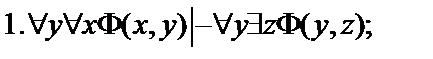
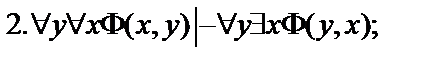
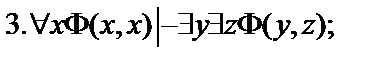
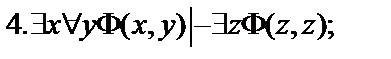
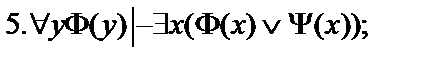
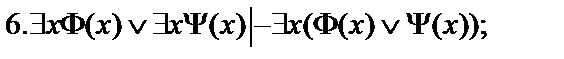
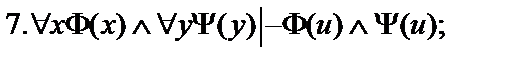
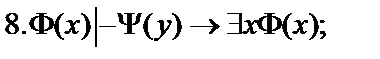
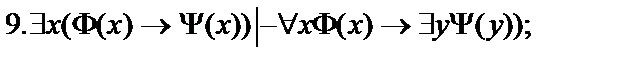
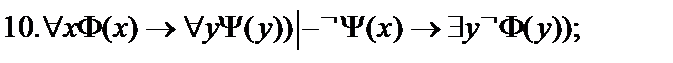
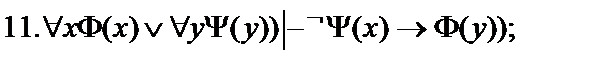
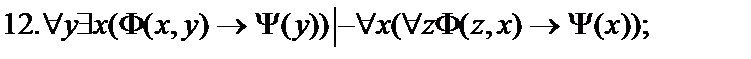
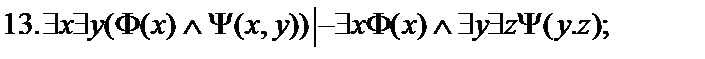
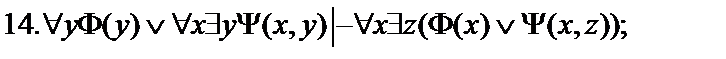
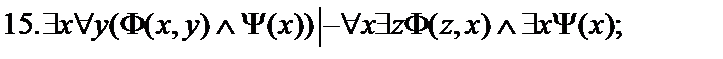
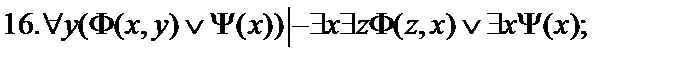
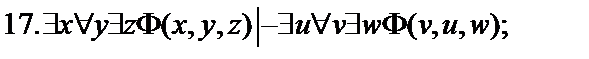
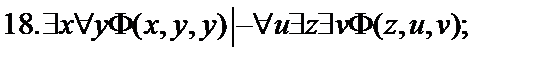
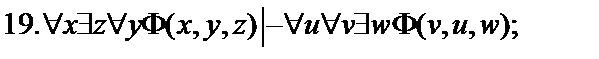
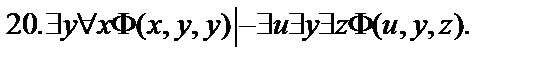
Пренексная нормальная форма
Пусть 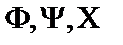 –атомарные формулы логики предикатов.Привести следующие формулы логики предикатов к пренексной нормальной форме.
–атомарные формулы логики предикатов.Привести следующие формулы логики предикатов к пренексной нормальной форме.
1. 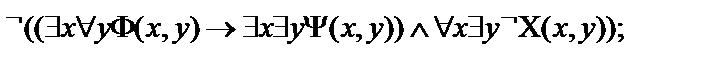
2. 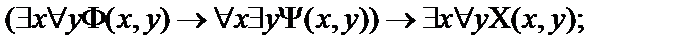
3. 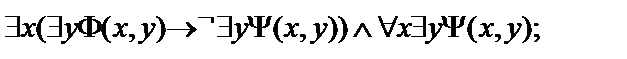
4. 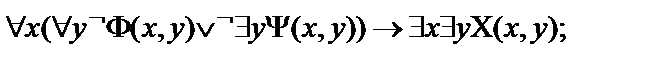
5. 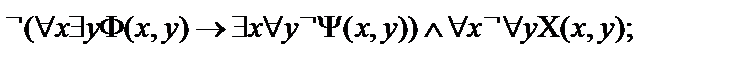
6. 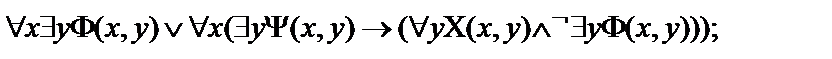
7. 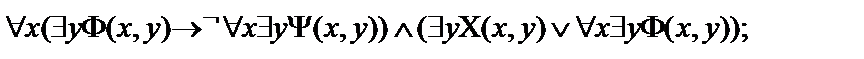
8. 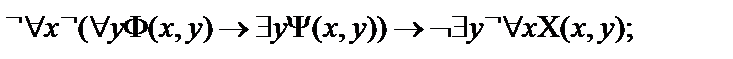
9. 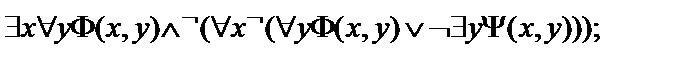
10. 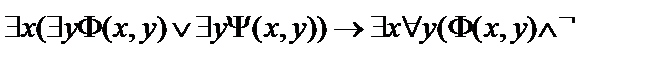
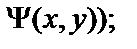
11. 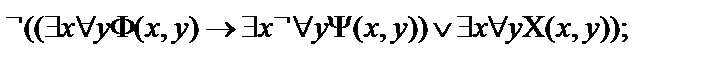
12. 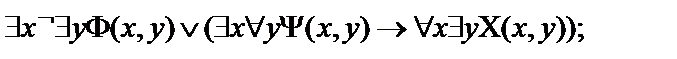
13. 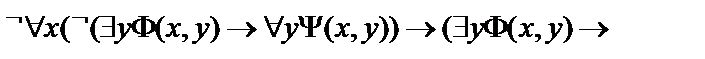
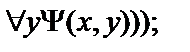
14. 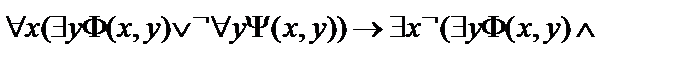
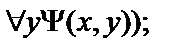
15. 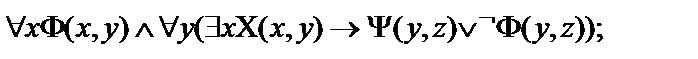 ,
,
16. 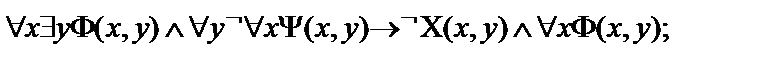
17. 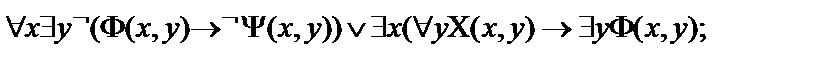
18. 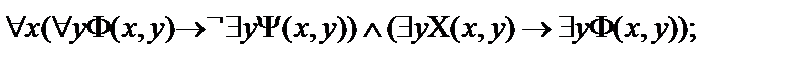
19. 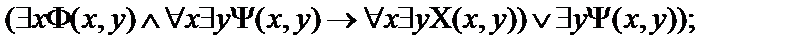
20. 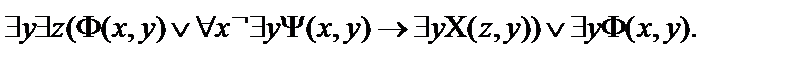
Машины Тьюринга
Построить машину Тьюринга  , вычисляющую следующую функцию.
, вычисляющую следующую функцию.
1. x+1;
2. x+y;
3. 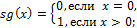
4. 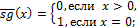
5. 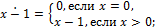
6. 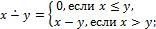
7. 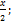
8.