Логика предикатов. Алгебраические системы
Часто объектом изучения в математике служит множество вместе с определенной на нем структурой. Например, поля, формирующие основу обычной арифметики, линейные пространства, обеспечивающие связь геометрических объектов с операциями над числами, множества с выделенными на них бинарными отношениями. Все эти структуры образуют алгебраические системы, представляющие собой некоторые миры с определенными на них законами. Перейдем к точному определению алгебраической системы.
Напомним, что п-местпным предикатом (отношением) на множестве А называется любое подмножество множества Аn; п-местной алгебраической операцией на множестве А называется функция ƒ:An→A, где Аn – n-я декартова степень множества А. Отметим, что поскольку операция ƒ является функцией, для любого набора (x1,…,xn)єAnрезультат применения операции ƒ(x1,…,xn)однозначно определен. Так как область значений операции ƒ лежит в множестве А, то будем говорить, что операция ƒ замкнута на множестве А.
Сигнатурой Σ называется совокупность предикатных и функциональных символов с указанием их местности. 0-местный функциональный символ называется константным символом или просто константой. Если α‑функциональный или предикатный символ, то его местность обозначается через μ(α)‑п-местные предикатные и функциональные символы часто будем обозначать соответственно через Р(n) и ƒ(n). Если в рассматриваемой сигнатуре используются стандартные символы, такие, например, как + для операции сложения, ≤ для отношения порядка, | для отношения делимости, 0 для константного символа и другие, то мы просто пишем Σ={≤}, Σ={≤,+, . , 0} и т.д.
Алгебраической системой A = 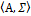 сигнатуры Σ называется непустое множество А, где каждому n-местному предикатному (функциональному) символу из Σ поставлен в соответствие n-местный предикат (соответственно операция) на А. Множество А называется носителем, или универсумом алгебраической системы
сигнатуры Σ называется непустое множество А, где каждому n-местному предикатному (функциональному) символу из Σ поставлен в соответствие n-местный предикат (соответственно операция) на А. Множество А называется носителем, или универсумом алгебраической системы 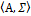 . Предикаты и функции, соответствующие символам из Σ, называются ихинтерпретациями. Обозначать интерпретации будем теми же буквами, что и соответствующие символы сигнатуры. Заметим, что интерпретацией любого константного символа является некоторый элемент из А.
. Предикаты и функции, соответствующие символам из Σ, называются ихинтерпретациями. Обозначать интерпретации будем теми же буквами, что и соответствующие символы сигнатуры. Заметим, что интерпретацией любого константного символа является некоторый элемент из А.
Пример 1.1) Набор  является алгебраической системой с двумя двухместными операциями.
является алгебраической системой с двумя двухместными операциями.
2) Набор  является алгебраической системой с бинарным отношением ≤, двухместными операциями +,
является алгебраической системой с бинарным отношением ≤, двухместными операциями +,  , одноместной операцией ' : п→n+1 и нуль-местной операций 1.
, одноместной операцией ' : п→n+1 и нуль-местной операций 1.
3) Набор 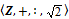 не является алгебраической системой, поскольку деление не является операцией на множестве Z, а элемент
не является алгебраической системой, поскольку деление не является операцией на множестве Z, а элемент  не принадлежит Z.
не принадлежит Z.
4) Набор 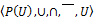 является алгебраической системой, где
является алгебраической системой, где 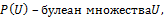 т.е. множество всех подмножеств множества
т.е. множество всех подмножеств множества 
5) Алгебраическая система  =(A,Σ) называется подсистемой системы
=(A,Σ) называется подсистемой системы 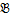 =(В, Σ) (обозначается
=(В, Σ) (обозначается 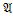
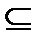
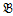 ), если выполняются следующие условия:
), если выполняются следующие условия:
а)А 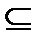 В;
В;
б)для любого функционального символа ƒ(n) 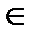 Σ соответствующих функций ƒA и ƒ ß и любых элементов a1,a2,…,an
Σ соответствующих функций ƒA и ƒ ß и любых элементов a1,a2,…,an 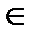 Aвыполняется равенство ƒA(a1,a2,…,an)=ƒß (a1,a2,…,an), т.е. интерпретации символа ƒ действуют одинаково на элементах из А;
Aвыполняется равенство ƒA(a1,a2,…,an)=ƒß (a1,a2,…,an), т.е. интерпретации символа ƒ действуют одинаково на элементах из А;
в)для любого предикатного символа Р(n) 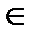 Σ, соответствующих предикатов
Σ, соответствующих предикатов 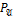 и
и 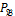 справедливо равенство P=
справедливо равенство P= 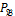 ∩An, т.е. предикат
∩An, т.е. предикат 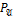 содержит в точности те кортежи предиката
содержит в точности те кортежи предиката 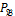 , которые состоят из элементов множества А.
, которые состоят из элементов множества А.
Теорема 1.Если 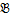 ‑алгебраическая система, X
‑алгебраическая система, X 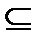 В, X≠Ø, то существует единственная подсистема
В, X≠Ø, то существует единственная подсистема 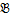 (Х)
(Х) 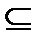
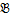 с носителем В(Х) такая, что X
с носителем В(Х) такая, что X 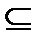 В(Х) и
В(Х) и 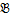 (Х)
(Х) 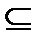
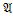 для любой подсистемы
для любой подсистемы 
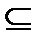
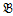 ,для которой X
,для которой X 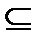 А.
А.
Доказательство.В качестве В(Х) рассмотрим пересечение носителей А всех подсистем 
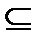
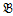 ,содержащих X. Так как X
,содержащих X. Так как X 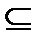 В(Х), то В(Х)≠Ø. Единственность подсистемы
В(Х), то В(Х)≠Ø. Единственность подсистемы 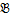 (Х) очевидна.
(Х) очевидна.
Подсистема 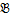 (Х) из теоремы 1 называется подсистемой, порожденной множеством Xв В.
(Х) из теоремы 1 называется подсистемой, порожденной множеством Xв В.
Для описания устройства подсистемы 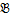 (Х) определим индукцией по построению понятие терма сигнатуры Σ:
(Х) определим индукцией по построению понятие терма сигнатуры Σ:
1) переменные и константные символы из Σ суть термы;
2) если ƒ 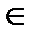 Σ‑n-местный функциональный символ, t1,t2,…,tn‑термы, то ƒ(t1,t2,…,tn)‑ терм;
Σ‑n-местный функциональный символ, t1,t2,…,tn‑термы, то ƒ(t1,t2,…,tn)‑ терм;
3) никаких термов, кроме построенных по пп. 1,2, нет.
Множество всех термов сигнатуры Σобозначается через Т(Σ).
Пример 2.
1) Термами сигнатуры Σ={+,∙,≤,0} будут, например, 0, x, x+y, z(x+z)+0y, а x+y≤(0+х)xтермом не является.
2) Если Σ={ƒ(3), g(1), h(2)}‑функциональная сигнатура, то выражения h(ƒ(x1, x2, x3), g(x2)), g(ƒ(h(x1, x2), x1, g(x2)) – термы, а h(x1, ƒ(x1, x3))не образует терм.
Пусть t(x1,…, xk)‑терм из T(Σ), все переменные которого содержатся среди x1,…,xk; 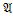 =(A,Σ)‑ алгебраическая система. Значение терма tпри значениях a1,…,ak
=(A,Σ)‑ алгебраическая система. Значение терма tпри значениях a1,…,ak 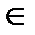 Aпеременных x1,…,xk(t(a1,…,ak)) определяется по индукции:
Aпеременных x1,…,xk(t(a1,…,ak)) определяется по индукции:
1) если tесть переменная xi(константный символ с), то значение tесть аi(с):
2) если терм tесть ƒ(t1,…, tn),а значения t1,…,tnсуть b1,…,bn, то значение терма tесть ƒ(b1,…, tn).
Теорема 2.Если 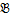 =(B,Σ)‑ алгебраическая система, Ø≠x
=(B,Σ)‑ алгебраическая система, Ø≠x 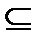 B, то носитель подсистемы
B, то носитель подсистемы 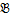 (Х) равен {t(a1,…,an)׀t
(Х) равен {t(a1,…,an)׀t 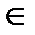 T(Σ), a1,…,an
T(Σ), a1,…,an 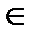 X}.
X}.
Доказательство.Индукцией по числу шагов построения терма tполучаем, что если t(x1,x2,…,xn) 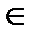 T(Σ) и a1,…,an
T(Σ) и a1,…,an 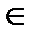 X, то t(a1,…,an)
X, то t(a1,…,an) 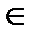 А для любой подсистемы
А для любой подсистемы 
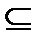
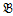 , содержащей X. Поэтому достаточно показать, что множество Y={t(a1,…,an)׀t
, содержащей X. Поэтому достаточно показать, что множество Y={t(a1,…,an)׀t 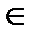 T(Σ), a1,…,an
T(Σ), a1,…,an 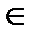 X} замкнуто относительно операций системы
X} замкнуто относительно операций системы 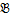 . Пустьƒ(n)єT(Σ), t1,…,tm
. Пустьƒ(n)єT(Σ), t1,…,tm 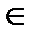 T(Σ), bi=t(a1,…,an), i
T(Σ), bi=t(a1,…,an), i 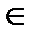 {1,…,m}. Тогдаƒ(b1,…,bm)
{1,…,m}. Тогдаƒ(b1,…,bm) 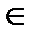 Y, посколькуƒ(t1,…,tm)
Y, посколькуƒ(t1,…,tm) 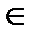 T(Σ).
T(Σ).
Таким образом, носитель подсистемы 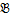 (X) состоит из всех элементов, которые получаются при подстановке элементов из Xв термы.
(X) состоит из всех элементов, которые получаются при подстановке элементов из Xв термы.
Пример 3.
1) Найдем носитель подсистемы 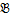 (Х) системы
(Х) системы 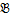 =(Q , ∙) для множества X={1/2}. Так как сигнатура Σ системы В есть {∙}, то Т(Σ)={x1, x1x2, (x1x2)x3, x1(x2x3),…}. По теореме 2 получаем B(X)={1/2, 1/2∙1/2, 1/2∙1/2∙1/2,…}={1/2, 1/8, 1/16,…}={1/2n,n≥1}.
=(Q , ∙) для множества X={1/2}. Так как сигнатура Σ системы В есть {∙}, то Т(Σ)={x1, x1x2, (x1x2)x3, x1(x2x3),…}. По теореме 2 получаем B(X)={1/2, 1/2∙1/2, 1/2∙1/2∙1/2,…}={1/2, 1/8, 1/16,…}={1/2n,n≥1}.
2)Если 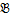 =(Q\{0}, . , : ) X={1/2}, то, поскольку по сравнению с предыдущим примером сигнатура дополняется операцией деления, множество В(Х) содержит числа 1/2n:1/2m=2m-n, m, n≥1, т.е. C={2n׀nєZ}
=(Q\{0}, . , : ) X={1/2}, то, поскольку по сравнению с предыдущим примером сигнатура дополняется операцией деления, множество В(Х) содержит числа 1/2n:1/2m=2m-n, m, n≥1, т.е. C={2n׀nєZ} 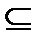 B(X).Так как множество С замкнуто относительно операций умножения и деления. т.е. (C, Σ) является подсистемой системы
B(X).Так как множество С замкнуто относительно операций умножения и деления. т.е. (C, Σ) является подсистемой системы 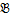 и содержит множество X, то В(Х)
и содержит множество X, то В(Х) 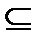 С. Следовательно, B(Х)=С.
С. Следовательно, B(Х)=С.
Пример 4. Построить подсистему алгебраической системы А, порожденную множеством Х.
 =
= 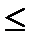 Z; -
Z; - 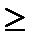
X={22;-36}.
Решение.Надо определить какую подсистему порождают
22;-36 “-“. Таке как 2=22-8  (-36)-14
(-36)-14  22 и любое число, получаемое из чисел 22, -36 с помощью операции вычитания четное, то
22 и любое число, получаемое из чисел 22, -36 с помощью операции вычитания четное, то
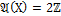
Пример 5. Построить подсистему алгебраической системы  , порожденнуюмножеством Х.
, порожденнуюмножеством Х.
 =
= 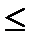 R\{0};:
R\{0};: 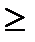
Х={ 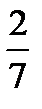 ;
; 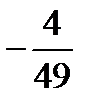 }.
}.
Решение.
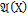 ={
={ 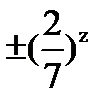 z
z 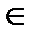 }.
}.
Формулы ЛП
Большинство определений этого параграфа будут индуктивными.
Введем понятие атомарной формулы сигнатуры Σ:
1) если t1, t2, 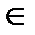 T(Σ), то t1=t2‑ атомарная формула:
T(Σ), то t1=t2‑ атомарная формула:
2) если P(n) 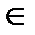 Σ‑предикатный символ, t1,t2,…,tn
Σ‑предикатный символ, t1,t2,…,tn 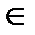 T(Σ), то Р(t1,t2,…,tn)‑ атомарная формула;
T(Σ), то Р(t1,t2,…,tn)‑ атомарная формула;
3) никаких атомарных формул, кроме построенных по пп. 1, 2, нет.
Формула сигнатуры Σ определяется следующим образом:
1) атомарная формула есть формула;
2) если φ, ψ - формулы, то φ, (φ∧ψ), (φ∨ψ), (φ→ψ),  xφ,
xφ,  xφ‑ формулы;
xφ‑ формулы;
3) никаких формул, кроме построенных по пп. 1, 2, нет.
Символы  ,
,  использованные в определении, называются соответственно квантором всеобщности и квантором существования и читаются "для любого"и "существует". Все соглашения относительно расстановок скобок, принятые в алгебре высказываний, остаются в силе и для формул логики предикатов. Кроме того, вместо записей
использованные в определении, называются соответственно квантором всеобщности и квантором существования и читаются "для любого"и "существует". Все соглашения относительно расстановок скобок, принятые в алгебре высказываний, остаются в силе и для формул логики предикатов. Кроме того, вместо записей  x1…
x1…  xnφи
xnφи  x1…
x1…  xnφбудем использовать записи
xnφбудем использовать записи  x1,…,xnφи
x1,…,xnφи  x1,…,xnφ.
x1,…,xnφ.
Определим подформулы формулы φсигнатуры Σ:
1) если φ‑атомарная формула, то φ‑ее единственная
подформула;
2) если φимеет вид φ1, или  xφ1,или
xφ1,или  xφ1, то подформула формулы φ–этолибо φ, либо подформула формулы φ1;
xφ1, то подформула формулы φ–этолибо φ, либо подформула формулы φ1;
3) если φимеет вид φ1∧φ2, или φ1∨φ2, или φ1→φ2, то подформула формулы φ‑ это либо φ, либо подформула формулы φ1, либо подформула формулы φ2;
4) других подформул формулы φ, кроме построенных по
пп. 1, 2, 3, нет.
Пример 1. Пусть Σ={F(2),P(1)}, φ=  x(
x(  y(x=F(z,y))∨P(z))‑ формула сигнатуры Σ. Тогда
y(x=F(z,y))∨P(z))‑ формула сигнатуры Σ. Тогда  x(
x(  y(x=F(z,y))∨P(z)),
y(x=F(z,y))∨P(z)),  y(x=F(z,y))∨P(z),
y(x=F(z,y))∨P(z),  y(x=F(z,y)),x=F(z,y)),P(z)‑все подформулы формулы φ.
y(x=F(z,y)),x=F(z,y)),P(z)‑все подформулы формулы φ.
Говорят, что вхождение переменной х в формулу φ связано в φ, если оно находится в терме или предикате подформулы формулы φвида  xψили
xψили  xψ; в противном случае это вхождение называется свободным в φ. Переменная х называется свободной (связанной), если некоторое вхождение х в φсвободно (связано).
xψ; в противном случае это вхождение называется свободным в φ. Переменная х называется свободной (связанной), если некоторое вхождение х в φсвободно (связано).
Пример 2. Пусть S={P1(1),P2(2)}. Рассмотрим формулы:
1) P1(x);
2) Р2(x,y)→  xP1(x);
xP1(x);
3)  x(P2(x,y)→P1(x)).
x(P2(x,y)→P1(x)).
Переменная х в первой формуле является свободной, во второй - и свободной, и связанной, в третьей ‑ связанной: переменная у во всех формулах свободна.
Пример 3.
Выписать все подформулы формулыφ, определить свободные и связанные вхождения переменных.
φ 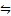
 x
x  z
z  y(x
y(x 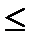 y+z)
y+z)  ((z∙2=u)→
((z∙2=u)→  u(u=x+z)).
u(u=x+z)).
Определить все свободные и связанные переменные формулы φ.
Решение. Выпишем подформулыформулы φ.
1) x 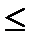 y+z,
y+z,
2)  y(x
y(x 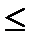 y+z),
y+z),
3)  z
z  y(x
y(x 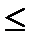 y+z),
y+z),
4)  x
x  z
z  y(x
y(x 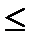 y+z),
y+z),
5) z  2=u,
2=u,
6) u=x+z,
7)  u(u=x+z),
u(u=x+z),
8) (z  2=u)→
2=u)→  u(u=x+z),
u(u=x+z),
9) φ.
Поскольку существуют связанные и свободные вхождения переменной х в формулу φ, то хявляется связанной и свободной переменной. Переменныеuи zтоже связанные и свободные. Переменнаяy связанная.
Предложением или замкнутой формулой сигнатуры Σ называется формула сигнатуры Σ, не имеющая свободных переменных.
Запись φ(x1,…,xn)будет означать, что все свободные переменные формулы φсодержатся в множестве {x1,…, xn}.
