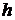Видно, что аргумент и модуль частотной передаточной функции являются функциями частоты.
C учетом (1.38) решение (1.36) принимает вид
 A(ω)
A(ω)  =
=  (1.39)
(1.39)
Далее необходимо выполнить второе решение от составляющей
 ωt.
ωt.
B этом случае решение уравнения (21) будем искать в виде
хвых2 = 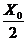 W(jω)e –jωt. (1.40)
W(jω)e –jωt. (1.40)
Дальнейший порядок получения решения не отличается от предыдущего, поэтому целесообразно сразу записать результат решения
 А(ω) e –j[ωt+y(ω)]. (1.41)
А(ω) e –j[ωt+y(ω)]. (1.41)
Для получения полного решения, отмеченный ранее принцип суперпозиции позволяет сложить полученные два решения (1.39) и (1.41)
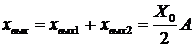 (ω) [e j[ωt+y(ω)] + e – j[ωt+y(ω)]].
(ω) [e j[ωt+y(ω)] + e – j[ωt+y(ω)]].
Далее, если опять применить формулу Эйлера, то нетрудно получить окончательный результат решения
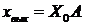 (ω) соs [ωt +y(ω)]. (1.42)
(ω) соs [ωt +y(ω)]. (1.42)
Сравнивая выражения, соответствующие входному (1.31) и выходному (1.42) сигналам можем отметить, что звено изменило входной сигнал. Действительно, амплитуда выходного сигнала отличается от амплитуды входного сигнала множителем А(ω). Величина А(ω) зависит от частоты входного сигнала ω. Кроме этого выходной сигнал в сравнении с входным сигналом смещен по фазе на угол y(ω). Величина этого угла также как и величина А(ω) зависит от частоты входного сигнала.
Зависимость А(ω) - амплитуды вынужденных колебаний выходного сигнала от частоты колебаний входного сигнала ω называется амплитудной частотной характеристикой (АЧХ) звена.
Амплитудная частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка делается по отношению амплитуд выходного и входного сигналов.
Зависимость y( 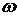 ) - смещение по фазе вынужденных колебаний выходного сигнала от частоты входного сигнала
) - смещение по фазе вынужденных колебаний выходного сигнала от частоты входного сигнала 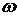 называется фазовой частотной характеристикой (ФЧХ) звена.
называется фазовой частотной характеристикой (ФЧХ) звена.
Фазовая частотная характеристика показывает фазовые сдвиги, вносимые звеном на различных частотах.
Выше указывалось, что частотная передаточная функция является комплексным числом (1.37). Следовательно, можем записать
 . (1.43)
. (1.43)
Модуль этого комплексного числа 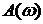 может быть найден как отношение модулей числителя и знаменателя ЧПФ
может быть найден как отношение модулей числителя и знаменателя ЧПФ
А( 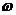 )=
)=  , (1.44)
, (1.44)
а его аргумент  – как разность обратных функций
– как разность обратных функций
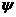 (
( 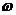 ) =
) = 


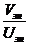 . (1.45)
. (1.45)
Для рассматриваемой частотной передаточной функции (1.31):
 и
и 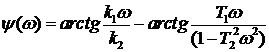 .
.
Амплитудно – фазовая частотная характеристика (АФЧХ) устанавливает математическую связь между двумя уже рассмотренными характеристиками АЧХ и ФЧХ. Характеристика строится на комплексной плоскости. Для построения используется частотная передаточная функция W(J 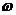 ) = U(
) = U( 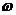 )+jV(
)+jV( 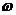 ). При изменении частоты от 0 ¸ ∞ изменяются мнимая и действительная составляющие ЧПФ. По оси абсцисс откладывается вещественная часть U(
). При изменении частоты от 0 ¸ ∞ изменяются мнимая и действительная составляющие ЧПФ. По оси абсцисс откладывается вещественная часть U( 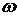 ) =Re W(j
) =Re W(j 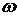 ) и по оси ординат – мнимая часть V(
) и по оси ординат – мнимая часть V( 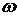 ) = Im W(j
) = Im W(j 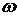 ). Для каждой частоты на комплексной плоскости наносится точка, рис. 1.27. Полученные точки соединяются плавной линией. Около нанесенных точек можно написать соответствующие им частоты
). Для каждой частоты на комплексной плоскости наносится точка, рис. 1.27. Полученные точки соединяются плавной линией. Около нанесенных точек можно написать соответствующие им частоты 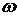 1,
1, 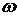 2,…,
2,…, 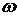 i…
i…

Построение АФЧХ можно выполнить и другим способом, используя для этого полярные координаты - модуль А( 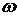 ) и смещение по фазе y(
) и смещение по фазе y( 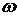 ). Зная модуль и смещение по фазе (или просто фазу) легко построить точку на комплексной плоскости. Данные о модуле и фазе для различных частот из диапазона 0 ¸ ∞ можно получать расчетом, используя для этого формулы (1.44) и (1.345) или использовать ранее построенные графики частотных характеристик А(
). Зная модуль и смещение по фазе (или просто фазу) легко построить точку на комплексной плоскости. Данные о модуле и фазе для различных частот из диапазона 0 ¸ ∞ можно получать расчетом, используя для этого формулы (1.44) и (1.345) или использовать ранее построенные графики частотных характеристик А( 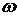 ) и y(
) и y( 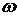 ).
).
Типовые динамические звенья
|
1.Позиционные звенья;
2.Дифференцирующие и интегрирующие звенья;
3.Трансцендентные звенья.
Для изучения свойств звеньев, в последующем материале установлен следующий порядок рассмотрения их характеристик: переходная характеристика, анализ; частотные характеристики, анализ.
4.1. Позиционные звенья
К позиционным звеньям относятся апериодическое звено первого и второго порядков, колебательное и консервативное звено.
Апериодическое звено 1 порядка. К этому типу звеньев относятся устройства, описываемые уравнением
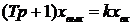 . (1.46)
. (1.46)
Передаточная функция звена 
Переходная характеристика получается, в результате решения уравнения
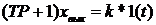 . (1.47)
. (1.47)
Решение состоит из суммы частного и общего решений. Общее решение получается из решения однородного уравнения 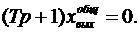 Это решение имеет вид
Это решение имеет вид 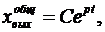 где
где  - корень уравнения
- корень уравнения 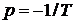 . Частное решение в соответствии с уравнением (1.47) имеет вид
. Частное решение в соответствии с уравнением (1.47) имеет вид 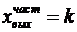 . Постоянная времени С находится из начальных условий. При
. Постоянная времени С находится из начальных условий. При 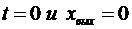 , следовательно, можно записать
, следовательно, можно записать 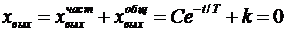 . Отсюда легко получить
. Отсюда легко получить  .
.
После сложения найденных решений получается полное решение
 .
.
На рис.1.28 изображено скачкообразное входное воздействие 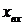
 =
=  (рис.1.28,а) и переходная функция
(рис.1.28,а) и переходная функция  (рис.1.28,б).
(рис.1.28,б).
Видно, что при изменении входной координаты (сигнала) на единицу выходная координата на новом установившемся режиме будет отличаться от исходного значения на величину коэффициента передачи звена  .
.

Изменения выходной координаты отстают от изменений входной координаты. При этом  не изменяется скачком, а плавно приближается к новому установившемуся положению по экспоненте (на рисунке экспонента выполнена с погрешностью). При этом, чем больше постоянная времени Т, тем медленнее координата
не изменяется скачком, а плавно приближается к новому установившемуся положению по экспоненте (на рисунке экспонента выполнена с погрешностью). При этом, чем больше постоянная времени Т, тем медленнее координата  приближается к установившемуся значению. Постоянная времени характеризует инерционное запаздывание
приближается к установившемуся значению. Постоянная времени характеризует инерционное запаздывание
апериодического звена. Практически принимается, что для апериодического звена время переходного процесса 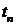 =(3¸5)Т. Величина постоянной времени Т определяется с помощью касательной, проведенной к экспоненте в произвольно расположенной точке «А».
=(3¸5)Т. Величина постоянной времени Т определяется с помощью касательной, проведенной к экспоненте в произвольно расположенной точке «А».
Частотные характеристики звена могут быть получены из выражения для частотной передаточной функции
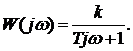 В соответствии с (1.44) и (1.45) можно записать выражения для АЧХ и ФЧХ:
В соответствии с (1.44) и (1.45) можно записать выражения для АЧХ и ФЧХ:
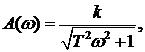 y
y  .
.
| |
| |
| |
| |
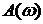 и
и  y
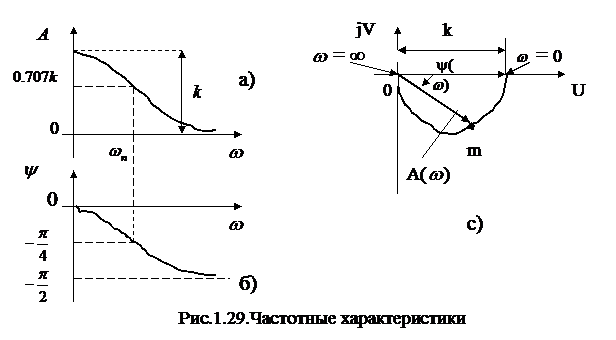
y  . Из графиков видно, что на малых частотах входной сигнал звеном пропускается с амплитудным усилением. Коэффициент усиления равен
. Из графиков видно, что на малых частотах входной сигнал звеном пропускается с амплитудным усилением. Коэффициент усиления равен  . Колебания на больших частотах происходят с большим ослаблением.
. Колебания на больших частотах происходят с большим ослаблением. Диапазон частот 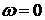 ¸
¸ 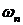 соответствует уменьшению усиления амплитуды до величины А = 0.707
соответствует уменьшению усиления амплитуды до величины А = 0.707  и называется полосой пропускания частот данного звена,
и называется полосой пропускания частот данного звена,  . Физически уменьшение амплитуды с ростом частоты обусловлено инерционностью звена.
. Физически уменьшение амплитуды с ростом частоты обусловлено инерционностью звена.
С увеличением частоты увеличивается отставание колебаний выходного сигнала звена от колебаний входного сигнала. На частоте  это отставание равно
это отставание равно  , а на больших частотах увеличивается до значения
, а на больших частотах увеличивается до значения  . Отставание выходных колебаний называется смещением по фазе и оно также обусловлено инерционностью звена.
. Отставание выходных колебаний называется смещением по фазе и оно также обусловлено инерционностью звена.
На рис.1.29,с изображена амплитудно - фазовая частотная характеристика звена. Форма АФЧХ – полуокружность. При построении АФЧХ частота колебаний 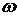 изменялась в интервале 0 ¸ ∞. Для каждой частоты из указанного интервала определялись значения
изменялась в интервале 0 ¸ ∞. Для каждой частоты из указанного интервала определялись значения 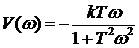 и
и 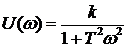 . Полученные данные наносились на график. Используя координаты точек графика АФЧХ, можно рассчитать соответствующие им значения
. Полученные данные наносились на график. Используя координаты точек графика АФЧХ, можно рассчитать соответствующие им значения 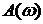 и y
и y  . Например, для точки
. Например, для точки 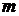 легко определяются
легко определяются 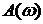 и y
и y  , а также и частота, соответствующая этой точки.
, а также и частота, соответствующая этой точки.
Колебательное звено. К этому типу звеньев относятся устройства, описываемые уравнением
 . (1.48)
. (1.48)
Передаточная функция звена
 .
.
Уравнение (1.48) удобно представить в виде
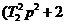 x
x 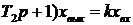 , (1.49)
, (1.49)
где x - параметр затухания колебаний, x = 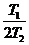 , ( 0 <
, ( 0 <  < 1).
< 1).
Переходная характеристика звена получается в результате решения уравнения
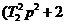 x
x 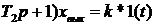 .
.
Решение этого уравнения также как и уравнения апериодического звена состоит из частного и общего решений
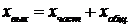 (1.50)
(1.50)
Частное решение 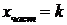 , общее решение имеет вид
, общее решение имеет вид
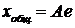 αt sin (
αt sin ( 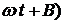 , (1.51)
, (1.51)
где α и 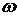 вещественная и мнимая составляющие комплексных корней характеристического уравнения
вещественная и мнимая составляющие комплексных корней характеристического уравнения
 x
x  = 0.
= 0.
Выражения для корней данного уравнения имеют вид
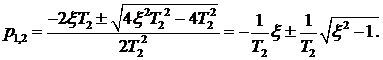
 (1.52)
(1.52)
Так как x < 1, то выражение под корнем является мнимым. Следовательно, корни комплексные, т.е.  α ±
α ± 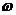 j, где j =
j, где j = 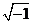 , α =
, α =  x,
x, 
Не выполняя дальнейших преобразований, запишем выражения для амплитуды А и фазы В: 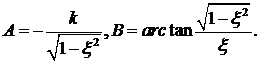

Далее уже можно получить вид зависимости для переходной характеристики (функции). Для этого используются частное решение. формулы (1.50),(1.51) и выражения для характеристик  и
и 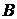
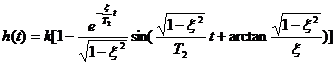 (1.53)
(1.53)

Видно, что переходная функция представляет собой затухающий колебательный процесс, рис 1.30. Колебательность  и скорость затухания процесса зависит от величины параметра затухания. На установившемся режиме ( при
и скорость затухания процесса зависит от величины параметра затухания. На установившемся режиме ( при  )
)  .
.

| |
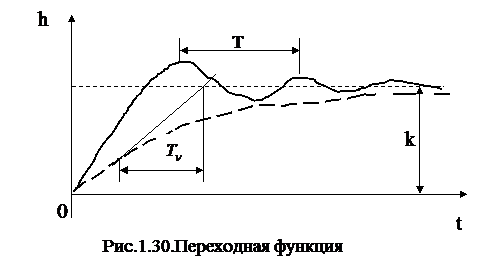
На рисунке пунктирной линией показана кривая, огибающая с одной стороны переходную характеристику. Эта кривая соответствует апериодическому процессу с постоянной времени \ 2 \
 =
=  .
.
Период колебаний переходной функции  . Если применить формулу для расчета частоты
. Если применить формулу для расчета частоты 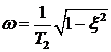 , то формула для расчета периода колебаний принимает вид
, то формула для расчета периода колебаний принимает вид  Из приведенных формул следует, что с уменьшением параметра
Из приведенных формул следует, что с уменьшением параметра  частота колебаний увеличивается, а период колебаний уменьшается. Время переходного процесса
частота колебаний увеличивается, а период колебаний уменьшается. Время переходного процесса  .
.
Если принять  , то окажется, что
, то окажется, что  и
и  . В этом варианте колебательное звено превращается в консервативное. Уравнение консервативного звена имеет вид
. В этом варианте колебательное звено превращается в консервативное. Уравнение консервативного звена имеет вид
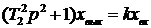 .
.
Выражение для переходной функции получается из формулы (1.53)
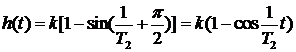
Видно, что переходной функции соответствуют незатухающие колебания с постоянной амплитудой. Частота колебаний 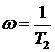 .
.
Если принять 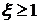 , то колебательное звено становится апериодическим второго порядка.
, то колебательное звено становится апериодическим второго порядка.
Очевидно, что уравнение звена по внешнему виду совпадает с уравнениями для колебательного звена (1.48) и (1.49). Однако, при 
 1 характеристическое уравнение звена имеет два вещественных корня (1.52). Поэтому передаточную функцию апериодического звена второго порядка оказывается возможным представить в виде двух последовательно соединенных передаточных функций, рис.1.31.
1 характеристическое уравнение звена имеет два вещественных корня (1.52). Поэтому передаточную функцию апериодического звена второго порядка оказывается возможным представить в виде двух последовательно соединенных передаточных функций, рис.1.31.
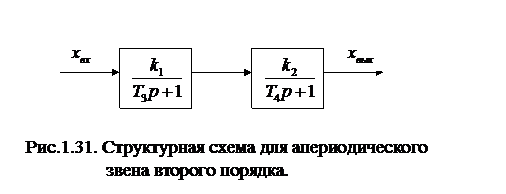
Коэффициенты 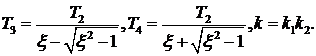 Выражение для переходной функции имеет вид
Выражение для переходной функции имеет вид
 (1.54)
(1.54)
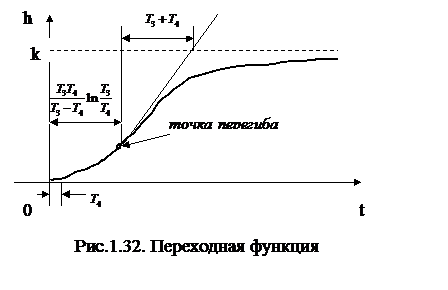
На рис.1.32 показан типовой вид переходной функции, соответствующий выражению (1.54). Видно, что колебания отсутствуют. Форма кривой переходного процесса в завершающей части похожа на форму переходной функции для апериодического звена первого порядка. Однако в начальной части форма кривой существенно отличается. В этой части кривая имеет точку перегиба, разделяющую части кривых, имеющих выпуклость и вогнутость.

Частотные характеристики колебательного звена также получаются из выражения частотной передаточной функции
| |
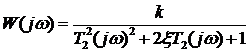 .
. В соответствии с (1.44) и (1.45) выражения для АЧХ и ФЧХ имеют вид:
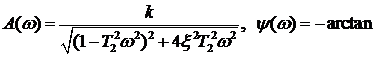
 .
.

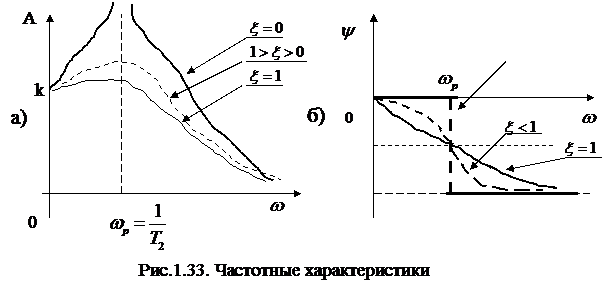
На рис.1.33,а представлены графики АЧХ, построенные для различных значений параметра затухания  . В случае, когда
. В случае, когда  выражение для АЧХ принимает вид
выражение для АЧХ принимает вид  . При резонансной частоте
. При резонансной частоте 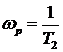 функция
функция 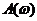 имеет разрыв, в котором
имеет разрыв, в котором  . Если
. Если  > 0, функция
> 0, функция 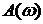 становится непрерывной. Если
становится непрерывной. Если  , то
, то 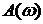 на резонансной частоте имеет максимум, при
на резонансной частоте имеет максимум, при  этот максимум отсутствует. Наличие максимума свидетельствует об усилении амплитуды в районе резонансных частот. На частотах
этот максимум отсутствует. Наличие максимума свидетельствует об усилении амплитуды в районе резонансных частот. На частотах  происходит ослабление амплитуды.
происходит ослабление амплитуды.
На рис. 1.33,б представлены графики  . Видно, что с увеличением частоты отставание изменения выходного сигнала от изменений входного сигнала увеличивается. При значении
. Видно, что с увеличением частоты отставание изменения выходного сигнала от изменений входного сигнала увеличивается. При значении  это отставание равно
это отставание равно  . Формы кривых
. Формы кривых  для вариантов
для вариантов  и
и  отличаются друг от друга в основном только кривизной. На рис.1.34,а изображен график АФЧХ колебательного звена.
отличаются друг от друга в основном только кривизной. На рис.1.34,а изображен график АФЧХ колебательного звена.
Примером колебательного звена может служить уравнение демпфера с пружиной, рис.1.34
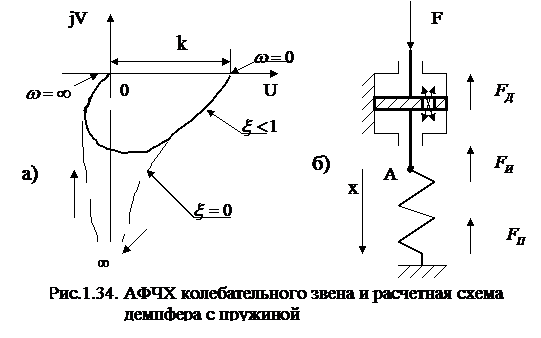
На рисунке представлена схема устройства. Схема содержит гидравлический цилиндр с поршнем. В поршне выполнено профилирующее отверстие для создания эффекта скоростного демпфирования, при движении поршня в цилиндре с вязкой жидкостью. Движение поршня вызывается действием силы 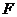 в направлении оси
в направлении оси  .
.
При составлении уравнения за выходную величину  (рис.1.34,а) примем перемещение точки
(рис.1.34,а) примем перемещение точки  . Входной величиной является сила
. Входной величиной является сила 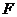 .
.
Пользуясь схемой можно составить уравнение равновесия сил, действующих в системе:
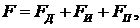
где: 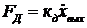 сила скоростного трения (
сила скоростного трения (  - коэффициент скоростного трения), возникающая в результате перетекания вязкой жидкости через калиброванное отверстие при перемещении поршня под действием силы
- коэффициент скоростного трения), возникающая в результате перетекания вязкой жидкости через калиброванное отверстие при перемещении поршня под действием силы 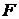 ;
;
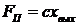 сила упругости пружины (с- коэффициент жесткости пружины);
сила упругости пружины (с- коэффициент жесткости пружины);
 инерционная сила,
инерционная сила, 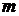 - масса подвижных частей, приведенных к точке А.
- масса подвижных частей, приведенных к точке А.
После несложных преобразований можем записать

где 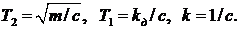
Далее несложно получить выражение для параметра затухания
 (1.55)
(1.55)
Из выражения (1.55) следует, что величина параметра затухания при заданной массе подвижных частей зависит от соотношения коэффициентов жесткости и скоростного трения. Если в рассматриваемом устройстве коэффициент скоростного трения  , то будут иметь место незатухающие колебания, так как при этом параметр затухания
, то будут иметь место незатухающие колебания, так как при этом параметр затухания  . Однако в механизмах скоростное трение всегда присутствует и поэтому на практике консервативные звенья не встречаются.
. Однако в механизмах скоростное трение всегда присутствует и поэтому на практике консервативные звенья не встречаются.
4.2. Дифференцирующее и интегрирующее звенья
Дифференцирующее звено. К этому типу звеньев относятся устройства описываемые уравнением
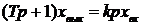 .
.
Передаточная функция имеет вид  .
.
Переходная характеристика получается в результате решения уравнения
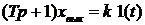 .
.
 Решение имеет вид:
Решение имеет вид: 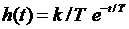 . График изменения переходной функции представлен на рис.1.35. Видно, что с течением времени кривая
. График изменения переходной функции представлен на рис.1.35. Видно, что с течением времени кривая  , убывая по экспоненте, стремится к нулю. При значении
, убывая по экспоненте, стремится к нулю. При значении 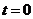 переходная функция
переходная функция 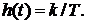
Частотные характеристики звена получаются из выражения частотной передаточной функции
 .
.

В соответствии с (1.44) и (1.45) выражения для АЧХ и ФЧХ получаются следующими: 
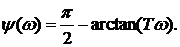
Графики характеристик представлены на рис.1.36.
На рис.1.36,а изображены амплитудно-частотные характеристики для идеального звена (Т = 0) и для инерционного (Т > 0). Видно, что идеальное звено усиливает амплитуду входного гармонического сигнала пропорционально увеличению частоты. Инерционное звено также усиливает амплитуду входного сигнала, но только до значения  . Фазовая частотная характеристика изображена на рис.1.36,б. Видно, что выходной сигнал всегда опережает сигнал на входе.
. Фазовая частотная характеристика изображена на рис.1.36,б. Видно, что выходной сигнал всегда опережает сигнал на входе.
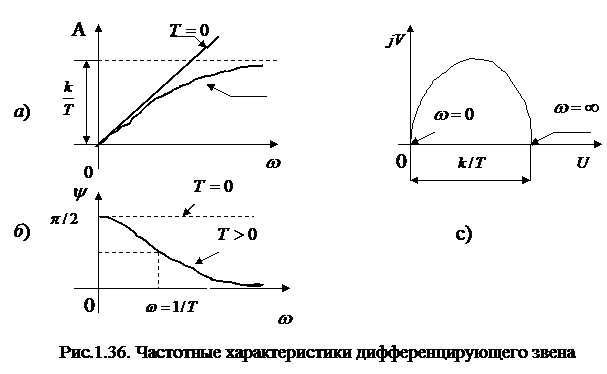
Однако, с увеличением частоты это опережение у инерционного звена непрерывно уменьшается. Идеальное же звено имеет постоянный угол опережения равный  . Можно заметить, что для инерционного звена есть участок относительно малых частот, где характеристики звена практически совпадают с характеристиками идеального звена. В связи с этим при относительно медленно меняющихся сигналах инерционное дифференцирующее звено можно рассматривать как идеальное. Такая замена упрощает исследование. На рис.1.36,с изображена амплитудно - фазовая частотная характеристика. Форма характеристики – полуокружность.
. Можно заметить, что для инерционного звена есть участок относительно малых частот, где характеристики звена практически совпадают с характеристиками идеального звена. В связи с этим при относительно медленно меняющихся сигналах инерционное дифференцирующее звено можно рассматривать как идеальное. Такая замена упрощает исследование. На рис.1.36,с изображена амплитудно - фазовая частотная характеристика. Форма характеристики – полуокружность.
Представителем дифференцирующего звена является тахогенератор (маломощный генератор) постоянного тока с возбуждением от постоянных магнитов, рис.1.37.

Применяется в системах регулирования в качестве корректирующего устройства.
Для получения уравнения тахогенератора необходимо записать
уравнение баланса напряжений в цепи якоря
 . (1.56)
. (1.56)
В соответствие с уравнением (1.56, электродвижущая сила 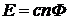 , вырабатываемая генератором, расходуется на падение напряжений на активном (
, вырабатываемая генератором, расходуется на падение напряжений на активном (  ) и индуктивном
) и индуктивном  сопротивлениях цепи якоря генератора.
сопротивлениях цепи якоря генератора.
Напряжение на зажимах генератора  .Далее
.Далее 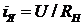 Дифференцируя левую и правую части этого уравнения, можно записать
Дифференцируя левую и правую части этого уравнения, можно записать
 (1.57)
(1.57)
С учетом (1.57) уравнение (1.56 можно записать в виде
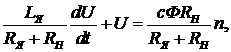
где с – постоянный коэффициент, зависит от конструкции ротора;
Ф – плотность магнитного потока возбуждения;
n - угловая скорость вращения ротора.
Вводя, оператор дифференцирования  , получим
, получим
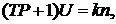 (1.58)
(1.58)
где 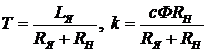 .
.
Так как угол поворота ротора и его угловая скорость связаны соотношением  , то уравнение (1.58) можно записать окончательном виде
, то уравнение (1.58) можно записать окончательном виде
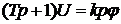 . (1.59)
. (1.59)
Уравнение (1.59) применяется в случае, когда тахогенератор используется в САР в качестве корректирующего элемента. В этом случае тахогенератор является дифференцирующим звеном. Уравнение (1.58) относится к апериодическому звену и применяется, когда тахогенератор используется в качестве датчика скорости вращения ротора.
Интегрирующее звено. К этому типу звеньев относятся устройства описываемые уравнением
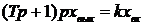 .
.
Передаточная функция имеет вид  .
.
Переходная характеристика звена получается в результате решения уравнения
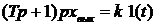 .
.
Не приводя последовательности решения, сразу запишем результат
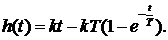
|

График переходной функции представлен на рис.1.38,а. Видно, что после завершения переходного процесса координата  изменяется с постоянной скоростью, несмотря на то, что на вход звена подан постоянный сигнал
изменяется с постоянной скоростью, несмотря на то, что на вход звена подан постоянный сигнал 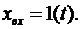 Время переходного процесса зависит от величины постоянной времени Т. Если постоянная времени
Время переходного процесса зависит от величины постоянной времени Т. Если постоянная времени  , переходная функция соответствует идеальному звену. Видно, что изменения координаты
, переходная функция соответствует идеальному звену. Видно, что изменения координаты  инерционного звена отстают от изменений координаты
инерционного звена отстают от изменений координаты  идеального звена. В переходном процессе отставание изменяется от 0 до
идеального звена. В переходном процессе отставание изменяется от 0 до  .
.
Частотные характеристики звена получаются из выражения для частотной передаточной функции
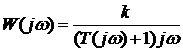 . (1.60)
. (1.60)
В соответствии с (1.44) формула для расчета АЧХ получается следующей
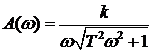 . (1.61)
. (1.61)
Для получения выражения ФЧХ преобразуем формулу (1.60). Умножим числитель и знаменатель на j. В результате получим
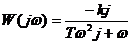
Далее применяя формулу (1.45) получаем выражение ФЧХ
 (1.62)
(1.62)
Графики АЧХ представлены на рис.1.38,б. На рисунке изображены два графика. Один из них соответствует идеальному звену  , другой – На рис.1.36,а изображены амплитудно-частотные характеристики для идеального звена (Т = 0) и для инерционного (Т > 0). Видно, что идеальное звено усиливает амплитуду входного гармонического сигнала пропорционально увеличению частоты. Инерционное звено также усиливает амплитуду входного сигнала, но только до значения
, другой – На рис.1.36,а изображены амплитудно-частотные характеристики для идеального звена (Т = 0) и для инерционного (Т > 0). Видно, что идеальное звено усиливает амплитуду входного гармонического сигнала пропорционально увеличению частоты. Инерционное звено также усиливает амплитуду входного сигнала, но только до значения  . Фазовая частотная характеристика изображена на рис.1.36,б. Видно, что выходной сигнал всегда опережает сигнал на входе. инерционному
. Фазовая частотная характеристика изображена на рис.1.36,б. Видно, что выходной сигнал всегда опережает сигнал на входе. инерционному  Видно, что графики похожи друг на друга. Отличие состоит лишь в том, что график, соответствующий инерционному звену располагается левее графика, соответствующего идеальному звену. Фазовая частотная характеристика изображена на рис.1.38,в. Видно, что в инерционном звене сдвиг по фазе превышает угол
Видно, что графики похожи друг на друга. Отличие состоит лишь в том, что график, соответствующий инерционному звену располагается левее графика, соответствующего идеальному звену. Фазовая частотная характеристика изображена на рис.1.38,в. Видно, что в инерционном звене сдвиг по фазе превышает угол 
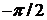 . Причем это превышение увеличивается с ростом частоты. Из графика ФЧХ также видно, что при малых частотах характеристика инерционного звена приближается к характеристике идеального звена. Это означает, что при уменьшении частоты управляющего сигнала влияние постоянной времени
. Причем это превышение увеличивается с ростом частоты. Из графика ФЧХ также видно, что при малых частотах характеристика инерционного звена приближается к характеристике идеального звена. Это означает, что при уменьшении частоты управляющего сигнала влияние постоянной времени 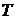 может быть уменьшено.
может быть уменьшено.
На рис.1.28,в изображен график АФЧХ. Для построения характеристики применены формулы для расчета мнимой и вещественной частей ЧПФ:


Видно, что при 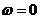 вещественная часть
вещественная часть 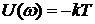 , а
, а 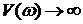 , а сдвиг по фазе
, а сдвиг по фазе 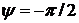 .
.
Представителями интегрирующих звеньев является большинство типов двигателей, применяющихся в автоматике. Получим передаточную функцию двигателя постоянного тока независимого возбуждения.
| | |||
| |

На рис.1.39 изображена схема якорной цепи двигателя. Определяя передаточную функцию двигателя, запишем дифференциальные уравнения, описывающие поведение двигателя в переходных процессах.
Напряжение, приложенное к якорю двигателя, уравновешивается падением напряжения на активном и индуктивном сопротивлениях якорной цепи и обратной электродвижущей силой (э.д.с.), возникающей при вращении якоря:

 , (1.63)
, (1.63)
где 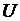 – напряжение, приложенное к цепи якоря двигателя;
– напряжение, приложенное к цепи якоря двигателя;
 - ток в цепи якоря;
- ток в цепи якоря;
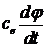 - напряжение обратной э.д.с.;
- напряжение обратной э.д.с.;
 - индуктивность цепи якоря;
- индуктивность цепи якоря;
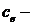 конструктивный коэффициент ;
конструктивный коэффициент ;
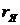 - активное сопротивление цепи якоря.
- активное сопротивление цепи якоря.
Дифференциальное уравнение движения якоря двигателя имеет вид
 , (1.64)
, (1.64)
где 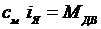 - вращающий момент двигателя;
- вращающий момент двигателя;
 коэффициент крутящего момента двигателя;
коэффициент крутящего момента двигателя;
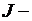 момент инерции нагрузки;
момент инерции нагрузки;
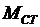 - статический момент нагрузки.
- статический момент нагрузки.
Передаточная функция двигателя получается в результате совместного решения уравнений (1.63) и (1.64). Если при решении уравнений принять 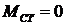 и перейти к операторной форме записи
и перейти к операторной форме записи 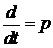 , то выражение передаточной функции получается следующим
, то выражение передаточной функции получается следующим
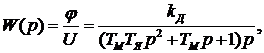 (1.65)
(1.65)
где  коэффициент передачи двигателя;
коэффициент передачи двигателя;
 электромеханическая постоянная времени;
электромеханическая постоянная времени;
 электромагнитная постоянная времени.
электромагнитная постоянная времени.
Величина электромеханической постоянной времени двигателя постоянного тока с независимым возбуждением находится в пределах 0.04 – 0.2 с. [4] Величина электромагнитной постоянной в несколько раз меньше электромеханической постоянной времени. В случаях, когда 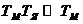 выражение (1.65) можно применять в виде
выражение (1.65) можно применять в виде
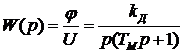 . (1.66)
. (1.66)
Выражение (1.65), как и выражение (1.66) является описанием интегрирующего звена. Отличие лишь в том, что в первом случае - интегрирующее звено второго порядка, а во втором случае – с интегрирующее звено первого порядка.
Если за выходную величину принять не угол поворота вала двигателя 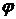 , а угловую скорость
, а угловую скорость 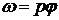 , то вместо выражений передаточных функций для интегрирующих звеньев (1.65) и (1.66) получатся выражения передаточных функций для апериодических звеньев первого и второго порядков
, то вместо выражений передаточных функций для интегрирующих звеньев (1.65) и (1.66) получатся выражения передаточных функций для апериодических звеньев первого и второго порядков
4.3. Трансцендентное звено
Звено «чистого» запаздывания. Уравнение для этого звена имеет вид
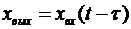 , (при t<
, (при t< 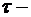
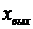 = 0), (1.67)
= 0), (1.67)
где 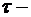 величина «чистого» запаздывания, рис.1.30. Рисунок отражает принцип работы звена. Видно, что после подачи сигнала на вход звена, сигнал на его выходе возникает только в момент времени
величина «чистого» запаздывания, рис.1.30. Рисунок отражает принцип работы звена. Видно, что после подачи сигнала на вход звена, сигнал на его выходе возникает только в момент времени  .
.
Правую часть уравнения (1.67) можно разложить в ряд Тейлора:
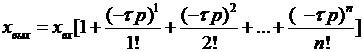 =
= 
Далее можно получить выражение для передаточной функции звена:
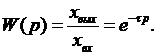 (1.68)
(1.68)

 Выражение для переходной функции получается из (1.67), если на вход звена подать сигнал
Выражение для переходной функции получается из (1.67), если на вход звена подать сигнал 
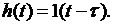
Графически переходная функция показана на рис.1.30,а.
Для определения частотных характеристик необходимо в выражении (1.68) выполнить замену  на произведение
на произведение 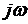 . После замены получим
. После замены получим 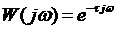 =
=  .
.
Далее можно записать выражения для мнимой и вещественной частей частотной передаточной функции:
 ,
,  (1.69)
(1.69)
Из выражений (1.69) нетрудно найти амплитудную и фазовую частотные характеристики:  ,
, 

На рис.1.31. изображены амплитудная фа