Синтез линейных автоматических систем
Задача 44. Разработать структурную схему системы автоматической регулирования уровня жидкости в рабочей емкости, рис.7.1.
На рисунке изображены рабочая и компенсационная емкости и схема прохождения окрашиваемой ткани. Объектом управления является рабочая емкость, в которой должен поддерживаться постоянный уровень жидкости h1. Примером такой емкости может служить плюсовка машины для непрерывного крашения тканей. В плюсовке должен поддерживаться постоянный уровень красильного раствора, что необходимо для стабильной пропитки ткани красильным раствором и для равномерной окраски ткани.
Унос красильного раствора из плюсовки обусловлен движущейся тканью с различной влажностью на входе в рабочую емкость 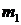 и на выходе из нее
и на выходе из нее 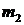 . Массовый расход ткани
. Массовый расход ткани 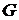 . Унос раствора тканью компенсируется подачей подкрепляющего раствора
. Унос раствора тканью компенсируется подачей подкрепляющего раствора 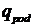 через клапан с проходным сечением
через клапан с проходным сечением 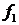 . Клапан играет роль регулирующего органа. Регулируемая величина – уровень жидкости в емкости
. Клапан играет роль регулирующего органа. Регулируемая величина – уровень жидкости в емкости 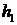 , регулирующее воздействие – изменение проходного сечения клапана
, регулирующее воздействие – изменение проходного сечения клапана 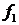 . Управляющее воздействие – заданная величина уровня жидкости в плюсовке
. Управляющее воздействие – заданная величина уровня жидкости в плюсовке 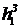 , которая преобразуется датчиком в электрический сигнал
, которая преобразуется датчиком в электрический сигнал  .
.
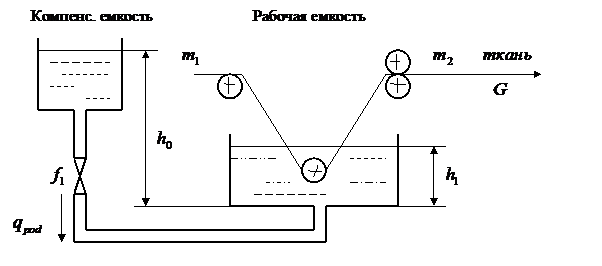
Рис. 7.1. Емкости для окрашивания тканей.
Задача 45.На рис.7.2 представлена структурная схема САР:
ЭУ - электронный усилитель, передаточная функция  ; МУ - магнитный усилитель, передаточная функция
; МУ - магнитный усилитель, передаточная функция 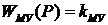 ;
;
ДВ - двигатель, является исполнительным элементом в системе, передаточная функция  =
=  ;
;
Р - редуктор, увеличивает мощность и понижает частоту вращения, вала двигателя передаточная функция 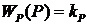 ;
;
РО - регулирующий орган, гидравлический вентиль с регулируемым проходным сечением f1 передаточная функция 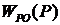 =
=  ;
;
ОУ - объект управления, передаточная функция  =
=  ;
; 
И - измеритель уровня раствора в емкости, передаточная функция 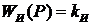 ;
;
ДОС - корректирующий элемент в цепи дополнительной обратной связи, передаточная функция 

Рис.7.2. Структурная сема системы.
Требуется получить уравнение системы в виде  .
.
Ответ: n=4, m=0; 

Упражнение 32.Структурная схема САР представлена на рис.7.3. Получить уравнение системы и построить рабочую область.
Исходные данные: 
Решение: Передаточная функция разомкнутой системы
 .
.
Передаточная функция замкнутой системы
 .
.
Уравнение системы
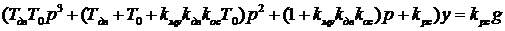 .
.

Рис. 7.3. Структурная схема САР
Уравнения границ для системы третьего порядка[ 2 ]
1. ;
;
2. 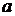 02
02 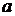 3 <= 1.05
3 <= 1.05 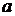 13; (7.1)
13; (7.1)
3. 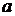 0
0 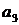 <= 0.5
<= 0.5 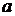 1
1 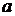 2;
2;
4. 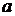 1
1 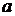 3 <= 6
3 <= 6 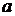 22.
22.
В соотношениях знак равенства предназначен для описания линий-границ, а знак неравенства - пространству с той стороны границ, где выполняются требования по запасу устойчивости.
Перед началом работы с соотношениями целесообразно определить численные значения параметров, образующих коэффициенты уравнения 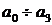 . В соответствии с исходными данным
. В соответствии с исходными данным
 0.15*0.1=0.015;
0.15*0.1=0.015;
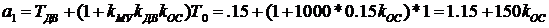 ;
;

С учетом полученных данных уравнения границ принимают вид:
1.  ;
;
2. 
3. 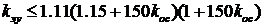 ;
;
4. 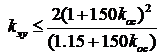 .
.
В результате анализа уравнений можно понять, что первое неравенство выполняется всегда при любых положительных значениях параметра 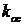 . Следовательно, описание этой границы можно исключить из рассмотрения.
. Следовательно, описание этой границы можно исключить из рассмотрения.
Неравенство, соответствующее второй границе для анализа можно упростить и записать его в виде
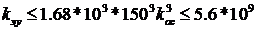
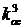
Трудно предположить, что в системе будут применяться усилители, с коэффициентом усиления 

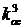 . Поэтому это неравенство также можно не рассматривать. Остаются неравенства 3 и 4.
. Поэтому это неравенство также можно не рассматривать. Остаются неравенства 3 и 4.
Расчет рабочей области целесообразно выполнить с помощью системы  . Ниже представлена возможная программа для расчета рабочей области по неравенствам 3 и 4. В конце программы составлены алгоритмы для контроля выполнения в рабочей области соотношений (7.1).
. Ниже представлена возможная программа для расчета рабочей области по неравенствам 3 и 4. В конце программы составлены алгоритмы для контроля выполнения в рабочей области соотношений (7.1).
