Лекция 21. оценка параметров генеральной совокупности

Функция распределения (плотность), математическое ожидание, дисперсия, мода и т.д. генеральной совокупности называются теоретическими характеристиками генеральной совокупности, а соответствующие характеристики, вычисляемые по выборке, называются выборочными (эмпирическими) характеристиками.

Под параметрами генеральной совокупности будем понимать как параметры законов распределения, так и числовые характеристики случайных величин. Оценка параметров генеральной совокупности по данным выборки – важнейшая задача статистики.

Обозначим параметр выборки буквой Θ. Вычисление Θ по всей генеральной совокупности затруднительно или невозможно. Поэтому о Θ пытаемся судить по случайной выборке, состоящей из значений х₁, х₂, …, х_n. Эти значения можно рассматривать как частные значения или реализации n независимых случайных величин Х₁, Х₂, …, Х_n, каждая из которых имеет тот же закон распределения, что и сама случайная величина Х. Оценку по выборке обозначим .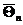

Определение 1. Оценкой 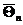параметра Θ называют всякую функцию результатов наблюдений над случайной величиной Х, которая в определенном статистическом смысле близка к истинному значению параметра Θ: 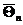= f(Х₁, Х₂, …, Х_n).

Так как Х₁, Х₂, …, Х_n – случайные величины, то и оценка 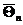– случайная величина (в отличие от Θ, которая является детерминированной).

Всегда существует несколько различных оценок одного и того же параметра.

Например, если Θ – математическое ожидание, то в качестве оценок среднего могут быть использованы .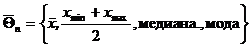

При этом возникает вопрос, какую из функций использовать в качестве оценки. Назвать «наилучшей» оценкой ту, которая наиболее близка к истинному значению оцениваемого параметра, невозможно. Это связано с тем, что 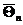– случайная величина и невозможно предсказать индивидуальные оценки в данном частном случае. Поэтому о качестве оценки судят не по ее индивидуальному значению, а лишь по распределению ее значений в большой серии испытаний, т.е. по выборочному распределению оценки. Рассмотрим ряд определений, которые характеризуют качество оценки с разных позиций.

Определение 2. Оценка 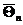параметра Θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е.

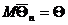. (11)

Определение 3. Оценка 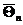параметра Θ называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходиться по вероятности к оцениваемому параметру:

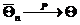или .

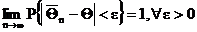Если оценка состоятельная, то оправдывается увеличение объема выборки для получения более точной оценки.

Теорема 1.Если оценка 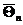параметра Θ является несмещенной, а ее дисперсия 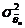стремится к нулю при n®¥, то оценка 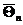– состоятельная.

Доказательство. Применим к 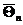следствие 1 из неравенства Чебышева, получим

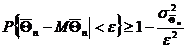, "e>0.

Но так как 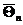– несмещенная оценка, то 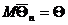и вероятность любого события больше либо равна единице, тогда имеем двойное неравенство

.

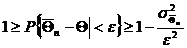Перейдя в данном неравенстве к пределу, получим 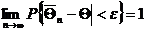,"e>0.

Определение 4.Оценка 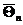параметра Θ называется эффективной, если она имеет наименьшую дисперсию 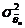среди всех возможных оценок параметра Θ, вычисленных по выборке одного и того же объема n, при этом

.

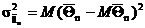Определение 5. Если для эффективной оценки выполнены условия

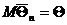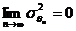и , то оценка называется абсолютно корректной или несмещенной состоятельной.

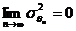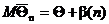Определение 6. Если оценка эффективная, и , , то оценка называется корректной или смещенной состоятельной.

Теорема 2.Среднее арифметическое является абсолютно корректной оценкой математического ожидания генеральной совокупности.

Доказательство. Пусть Х – генеральная совокупность и МХ= 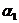= , X₁, X₂, …, X_n – выборка из генеральной совокупности. Из определения выборки следует, что X_i – независимы и МX_i= 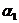, DX_i = s², тогда

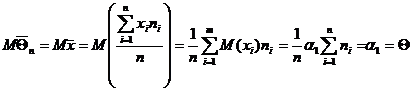, следовательно .

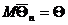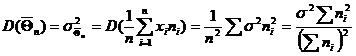, из анализа известно, что 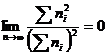, поэтому 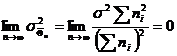. Учитывая, что является также и эффективной оценкой, получим, что среднее арифметическое является абсолютно корректной оценкой математического ожидания.

Теорема 3.Выборочная дисперсия является корректной или смещенной состоятельной оценкой дисперсии генеральной совокупности. Покажем справедливость теоремы для несгруппированного ряда.

Пусть 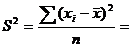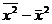. Найдем математическое ожидание MS².

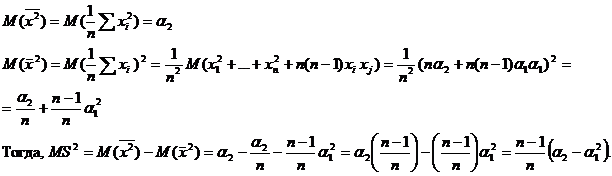Следовательно, MS² = 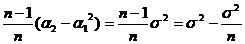, т.е. MS² = 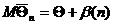, где 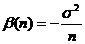– бесконечно малая величина. Таким образом, мы показали, что выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности.

Можно показать, что она является эффективной и 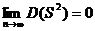, тогда получим, что выборочная дисперсия является корректной или смещенной состоятельной оценкой дисперсии генеральной совокупности.

В то же время легко видеть, что 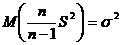. Поэтому, если в качестве выборочной дисперсии использовать оценку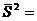 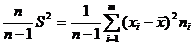, то она будет абсолютно корректной оценкой дисперсии генеральной совокупности.

Можно показать, что эмпирические плотность распределения и функция распределения при 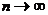становятся сколь угодно близкими к теоретическим, т.е. они являются состоятельными оценками. По этой же причине выборочные моменты случайных величин также являются состоятельными оценками. Данное свойство лежит в основе метода моментов точечной оценки параметров распределения.