Свойства среднеквадратического отклонения

1. .

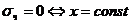2. .

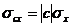3.Если X, Y – независимые случайные величины, то .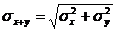

4.

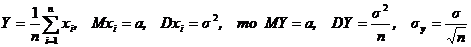
Определение 3. Случайная величина X называется нормированной (стандартизованной), если MX = 0, DX = 1.

Определение 4. Преобразование случайной величины вида 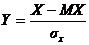называется нормированием случайной величины.

Убедимся в том, что случайная величина вида 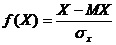является нормированной

.

.

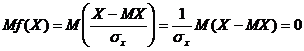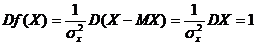Следует заметить, что f(X) – безразмерная величина, не зависит от масштаба измерения исходной случайной величины.

Еще одной безразмерной характеристикой степени разброса случайной величины, не зависящей от масштаба измерения, является коэффициент вариации V_x

.

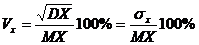ЛЕКЦИЯ 15. ВЫЧИСЛЕНИЕ ДИСПЕРСИИ ОСНОВНЫХ РАСПРЕДЕЛЕНИЙ

Пусть m_n – число успехов в n испытаниях Бернулли. Представим m_n в виде суммы

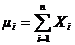, где Х_i – число успехов в i-м испытании. Очевидно, что Х_i принимает значения 0 или 1. Ранее было показано, что MX_i = p. Найдем DX_i, воспользовавшись формулой

.

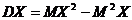Далее в таблицах приведены распределения Х_i и Х_i²

Xi
pi	1-p	p

Xi2
pi	1-p	p

Легко видеть, что MX_i² = 0+1p = p, тогда DX_i = p – p² = p(1-p) = pq.

Следовательно,

Dm_n = D 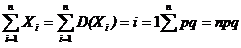. (1)

Нормальное распределение

Пусть X имеет нормальное распределение. Раннее, в лекции 11 (пример 2) было показано, что если

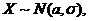
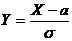, то Y ~ N(0,1).

Отсюда 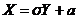, и тогда 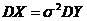, поэтому найдем сначала DY.

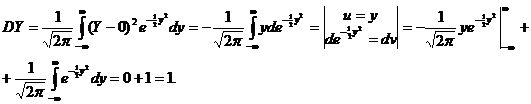
Следовательно

DX = D(sY+a) = s²DY = s², s_x = s. (2)

Экспоненциальное распределение

Плотность распределения имеет вид .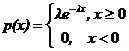

Ранее мы показали, что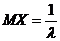. Для нахождения дисперсии воспользуемся формулой .

,

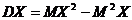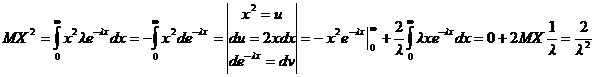тогда

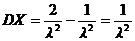(3)

Распределение Пуассона

Как известно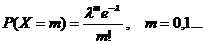

Ранее мы показали, что 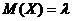, воспользуемся формулой .

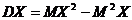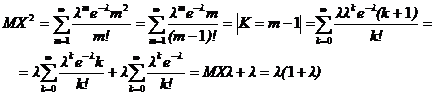
Следовательно,

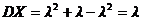(4)

Равномерное распределение

Известно, что .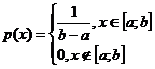

Ранее мы показали, что 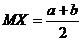, воспользуемся формулой .

,

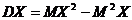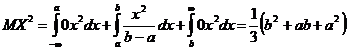тогда

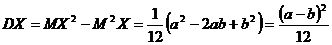. (5)

Моменты случайной величины. Характеристики формы распределения

Определение 1. Начальным моментом k-го порядка случайной величины Х называется число, равное математическому ожиданию случайной величины Х^к : 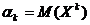, k = 1, 2, …

Из этого определения следует, что математическое ожидание случайной величины является начальным моментом 1-го порядка, так как a₁ = М(Х).

Определение 2.Центральным моментом k-го порядка называется число, равное математическому ожиданию k-й степени отклонения случайной величины от своего математического ожидания: .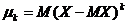

При k = 1, , ;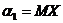

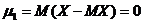при k = 2, .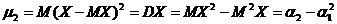

Теорема 1. Если многоугольник распределения дискретной случайной величины или плотность распределения непрерывной случайной величины симметричны относительно прямой х = MX, то все центральные моменты нечетного порядка равны нулю, т.е. m_2к+1 = 0. Докажем это утверждение для непрерывной случайной величины.

Доказательство.

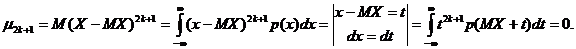
Последний интеграл в цепочке равенств равен 0, так как из условия задачи следует, что p(MX+t) – четная функция относительно t (p(MX+t) = p(MX-t)), а t^2k+1 – нечетная функция.

Так как плотности нормального и равномерного законов распределений симметричны относительно х = МХ, то все центральные моменты нечетного порядка равны 0.

Теорема 2.Если X~N(a,s), то .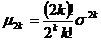

Чем больше моментов случайной величины известно, тем более детальное представление о законе распределения мы имеем. В теории вероятностей и математической статистике наиболее часто используются две числовые характеристики, основанные на центральных моментах 3-го и 4-го порядков. Это коэффициент асимметрии и эксцесс случайной величины.

Определение 3. Коэффициентом асимметрии случайной величины Х называется число b = .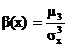

Коэффициент асимметрии является центральным и начальным моментом нормированной случайной величины Y, где 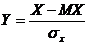. Справедливость этого утверждения следует из следующих соотношений:

.

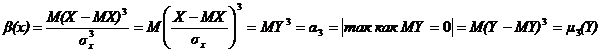Асимметрия случайной величины Х равна асимметрии случайной величины Y = αХ + β

c точностью до знака α, 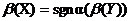. Это следует из того, что нормирование случайных величин aХ+ b и Х приводит к одной и той же случайной величине Y с точностью до знака

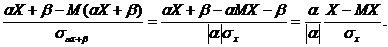
Если распределение вероятностей несимметрично, причем «длинная часть» графика расположена справа от центра группирования, то β(х) > 0; если же «длинная часть» графика расположена слева, то β(х) < 0. Для нормального и равномерного распределений β = 0.

В качестве характеристики большей или меньшей степени «сглаженности» кривой плотности или многоугольника распределения по сравнению с нормальной плотностью используется понятие эксцесса.

Определение 4. Эксцессом случайной величины Х называется величина

g = .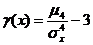

Эксцесс случайной величины Х равен разности начального и центрального моментов 4-го порядка нормированной случайной величины 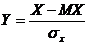и числа3, т.е. 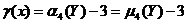. Покажем это:

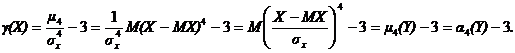
Эксцесс случайной величины Х равен эксцессу случайной величины

Y = αХ + β.

Найдем эксцесс нормальной случайной величины Х.

Если Х~N(a,s), то 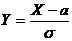~ (0,1).

Тогда

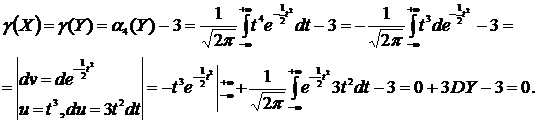
Таким образом, эксцесс нормально распределенной случайной величины равен 0. Если плотность распределения одномодальна и более «островершинна», чем плотность нормального распределения с той же дисперсией, то g(Х) > 0, если при тех же условиях менее «островершинна», то g(Х) < 0.