Лекция 5. распределения дискретных случайных величин

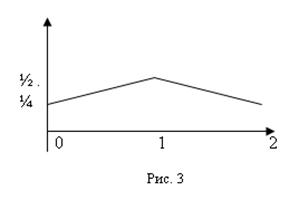
Дискретная случайная величина принимает конечное или счётное множество значений. Пусть Х – дискретная случайная величина, принимающая значения x₁ < x₂ < …< x_n … с вероятностями р₁, р₂, …., р_n ,…, Р(x_i) = p_i, . Если по оси абсцисс отложить x₁, x₂, …, x_n …, а по оси ординат – соответствующие вероятности p_i и соединить соседние точки отрезками, то получим многоугольник распределения дискретной случайной величины (рис.1), который является графическим изображением ряда распределения дискретной случайной величины. Например, если Х – число выпадений «решки» при двух подбрасываниях монеты, то ряду распределения, изображенному на рис. 2 будет соответствовать многоугольник распределения, изображенный на рис. 3.

хi
pi	0.25	0.5	0.25

Рис. 1 Рис.2

Рассмотрим, что представляет собой функция распределения дискретной случайной величины Х.

Если х £ х₁ , то F(x) = P(X< x)= 0, так как событие {w: X< x} – невозможное.

Если х₁ < х £ х₂, то событие {w: X< x} наступит тогда и только тогда, когда наступит событие {w: X = x₁}, поэтому F(x) = P(X< x) = Р {X = x₁} = р₁.

Если х₂ < х £ х₃ , то событие {w: X< x} равно сумме событий {w: X = x₁}и {w: X = x₂}. Поэтому F(x) = P(X< x) = Р {X = x₁} + Р {X = x₂} = р₁ + р₂.

Аналогично, если х_i < х £ х_i+1, то F(x) = р₁ +р₂+…+р_i.

Таким образом, функция распределения дискретной случайной величины имеет вид

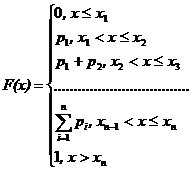
Очевидно, что функция распределения дискретной случайной величины постоянна на промежутках (-¥, х₁], (х₁, х₂], …, (х_i, х_i+1], … В точках x₁, x₂, …, x_n …, функция распределения имеет скачки, равные вероятности того, что случайная величина примет соответствующее значение. График функции распределения будет иметь вид, схематично изображенный на рис. 4. График функции распределения, соответствующий ряду распределения числа выпадений «решки», изображен на рис. 5.

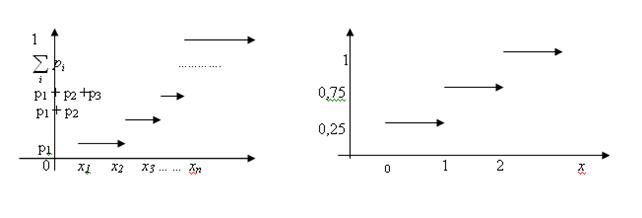
Рис. 4 Рис. 5

Основные дискретные распределения случайных величин

Равномерное распределение

Определение 1. Случайная величина Х, принимающая значения 1, 2, …, n, имеет равномерное распределение, если P_m = P(Х = m) = 1/n,

m = 1, …, n.

Очевидно, что .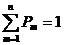

Рассмотрим следующую задачу.В урне имеется N шаров, из них M шаров белого цвета. Наудачу извлекается n шаров. Найти вероятность того, что среди извлечённых будет m белых шаров.

Нетрудно видеть, что .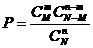

Гипергеометрическое распределение

Определение 2.Случайная величина Х, принимающая целочисленные значения, имеет гипергеометрическое распределение, если 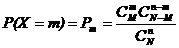, m = 0, 1, …, min(n, M). Можно показать, что .

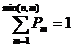Геометрическое распределение

Определение 3.Случайная величина X имеет геометрическое распределение, если

P(Х = m) = P_m= q^m-1p, m = 1, …

где q = 1–p, pÎ(0, 1). Геометрическое распределение имеет случайная величина X, равная числу испытаний по схеме Бернулли до первого наступления успеха с вероятностью успеха в единичном испытании р. Покажем, что Σp_i = 1

.

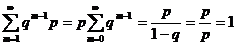Распределение Пуассона

Определение 4. Случайная величина Х имеет распределение Пуассона с параметром l, если 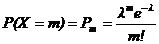, m = 0, 1, …

Покажем, что Σp_m = 1. .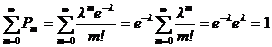

Биномиальное распределение

Определение 5.Случайная величина X имеет биномиальное распределение, если 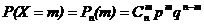, m = 0, 1, …, n,

где n – число испытаний по схеме Бернулли, m – число успехов, р – вероятность успеха в единичном исходе, q = 1–p.

Распределение Бернулли

Определение 6.Случайная величина Х имеет распределение Бернулли, если P(Х = m) = P_m = p^mq^n-m, m = 0, 1, …, n.

При больших m и n становится проблематичным вычисление по формуле Бернулли. Поэтому в ряде случаев удается заменить формулу Бернулли подходящей приближенной асимптотической формулой. Так если n – велико, а р мало, то .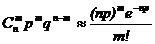

Теорема Пуассона. Если n ® ¥, а p ® 0, так что np ® l, то .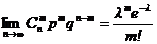

Доказательство. Обозначим l_n = np, по условию теоремы 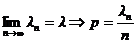, тогда

.

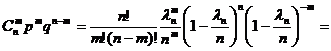
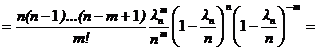
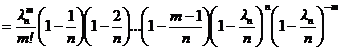При n ® ¥, l_n^m ® l^m,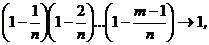

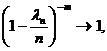
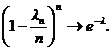
Отсюда получаем утверждение теоремы. Р_n(m) ® 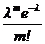при n ® ¥.

Формула Пуассона хорошо приближает формулу Бернулли, если npq £ 9. Если же произведение npq велико, то для вычисления Р_n(m) используют локальную теорему Муавра–Лапласа.

Локальная теорема Муавра – Лапласа.Пусть pÎ(0;1) постоянно, величина 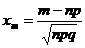равномерно ограничена, т.е. $с, |x_m|<с. Тогда

,

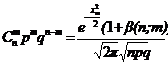где b(n;m) – бесконечно малая величина, причем .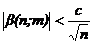

Из условий теоремы следует, что ,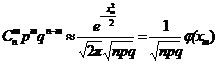

где , .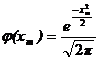

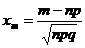Для вычисления Р_n(m) по формуле, приведенной рнее, используют таблицы функции

.

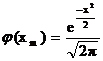Задача 1. В магазин одежды один за другим входят трое посетителей. По оценкам менеджера, вероятность того, что вошедший посетитель совершит покупку, равна 0,3. Составить ряд числа посетителей, совершивших покупку.

Решение.

xi
рi	0,343	0,441	0,189	0,027

Задача 2. Вероятность поломки произвольного компьютера равна 0,01. Построить ряд распределения числа вышедших из строя компьютеров с общим числом 25.

Решение.

xi								…
рi (Пуассон)	0,778	0,196	0,024	0,002	0,000	0,000	0,000	0,000	0,000
рi (Бернулли)	0,779	0,195	0,022	0,001	0,000	0,000	0,000	0,000	0,000

Задача 3. Автомобили поступают в торговый салон партиями по 10 шт. В салоне подвергаются контролю качества и безопасности только 5 из 10 поступивших автомобилей. Обычно 2 из 10 поступивших машин не удовлетворяют стандартам качества и безопасности. Чему равна вероятность, что хотя бы одна из 5 проверяемых машин будет забракована.

Решение. Р = Р₍₁₎ + Р₍₂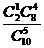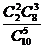₎ = + =0,5556 + 0,2222 = 0,7778