Основные свойства б.м. и б.б. последовательностей

Определение предела по Коши и Гейне

Пусть функция f(x) определена на некотором открытом интервале X, содержащем точку x=a. (При этом не требуется, чтобы значение f(a) было обязательно определено.)

Число L называется пределом функции f(x) при x→a, если для каждого ε>0 существует такое число δ>0, что|f(x)−L|<ε,при условии0<|x−a|<δ.Данное определение предела известно как ε−δ− определение или определение Коши.

Существует также определение предела функции по Гейне, согласно которому функция f(x) имеет предел L в точке x=a, если для каждой последовательности {xn}, сходящейся к точке a, последовательность f(xn) сходится к L. Определения предела функции по Коши и Гейне эквивалентны.

Односторонние пределы

Символом limx→a−0 обозначается левосторонний предел, в котором переменная x, приближаясь к a, принимает значения x<a. Соответствующий предел limx→a−0f(x) называется левосторонним пределом функции f(x) в точке x=a.

Аналогично, символом limx→a+0 обозначается правосторонний предел, в котором переменная x, приближаясь к a, принимает значения x>a. Соответствующий предел limx→a+0f(x) называется правосторонним пределом функции f(x) в точке x=a.

Отметим, что двусторонний предел limx→af(x) существуют лишь тогда, когда существуют оба односторонних предела, которые равны друг другу, то есть limx→a−0f(x)=limx→a+0f(x). В этом случаеlimx→af(x)=limx→a−0f(x)=limx→a+0f(x).

Билет №11. Первый замечательный предел.

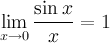
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

Следствия из первого замечательного предела

1°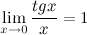

2°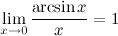

3°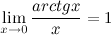

4°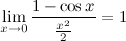

Билет №12. Второй замечательный предел.

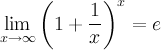
здесь е - число Эйлера.

Теорема Коши о промежуточном значении непрерывных функций

Теорема.
Если функция ff непрерывна на отрезке [a,b][a,b], A=f(a)≠f(b)=BA=f(a)≠f(b)=Bи число CC заключено между числами AA и BB, то существует такая точка c∈[a,b]c∈[a,b], что f(c)=Cf(c)=C.
Доказательство.
Не нарушая общности будем считать, что A=f(a)<f(b)=BA=f(a)<f(b)=B. Рассмотри функцию h(x)=f(x)−Ch(x)=f(x)−C, непрерывность на отрезке [a,b][a,b] которой следует из непрерывности функции ff. Очевидно что h(a)=A−C<0h(a)=A−C<0 и h(b)=B−C>0h(b)=B−C>0. Применяем к hh первую теорему Коши и находим точку cc в которой h(c)=f(c)−C=0h(c)=f(c)−C=0, то-есть f(c)=Cf(c)=C. Теорема доказана.
Геометрический смысл теоремы.
Как мы видим на рисунке изображен график функции f(x)f(x)(в общем произвольной), непрерывной на отрезке [a,b][a,b], где f(b)<f(a)f(b)<f(a), CC произвольная точка на отрезке [f(b),f(a)][f(b),f(a)] и прямая ll задана формулой l(x)=Cl(x)=C. Как мы видим, прямая ll обязана пересечь кривую f(x)f(x) в какой-то точке MM, лежащей на кривой f(x)f(x), между точками A(a,f(a))A(a,f(a)) и B(b,f(b))B(b,f(b)). То-есть существует такое c∈[a,b]c∈[a,b], что f(c)=Cf(c)=C.

Утверждение 1

Рассмотрим многочлен степени 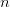, т. е. функцию вида

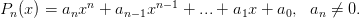
Эта функция непрерывна на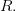

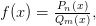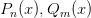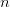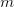Рациональная функция, т. е. функция вида где — многочлены степени и соответственно, непрерывна во всех точках, которые не являются нулями многочлена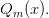

Утверждение 2

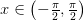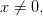Если и то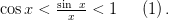

Следствие

Первый замечательный предел

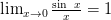
Утверждение 3

Для всех 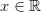справедливо неравенство

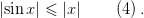
Утверждение 4

Функци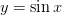и и 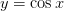непрерывны на всем множестве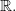

Следствие

Функция 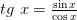– непрерывная при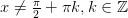

Утверждение 5

Рассмотрим несколько функции с их графиками

1. 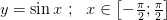строго возрастает и непрерывна

2. 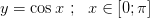строго спадает и непрерывна

3. 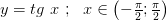строго возрастает и непрерывна

4. 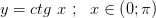строго спадает и непрерывна

Тогда по теореме существуют обратные непрерывные монотонные функции соответственно

1.

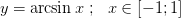
2.

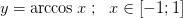
3.

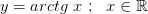
4.

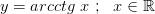
Утверждение 6

Функция 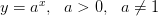– монотонна непрерывна на 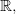то есть

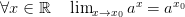
и тогда функция 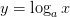– монотонна и непрерывна(как обратная)

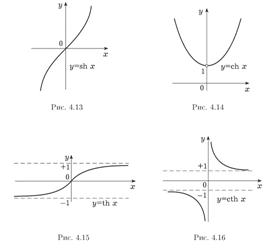
Утверждение 7

Функции, заданные формулами

называют соответственно гиперболическим синусом и гиперболическим косинусом.

Эти функции определены и непрерывны на 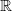, причем 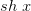— нечетная функция, а 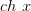– четная функция.

Из определения функци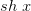й и 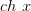следует, что

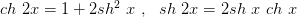
По аналогии с тригонометрическими функциями гиперболические тангенс и котангенс определяются соответственно формулами

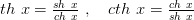
Функция 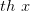определена и непрерывна на 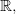а функция 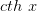определена и непрерывна на множестве 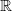с выколотой точкой 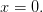Обе функции нечетные.

Утверждение 8

Пусть функци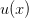и и 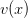определены на промежутке 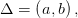причем для всех 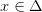выполняется условие 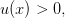Тогда функцию 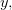определяемую формулой

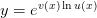
будем называть показательно-степенной и обозначать

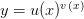
Таким образом, исходя из определения

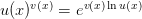
Если 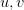— функции, непрерывные на 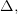то функция 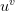непрерывна на 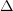как суперпозиция непрерывных функци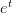й и .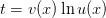

Билет №21.Обратные тригонометрические функции и их свойства.

Функция arcsin

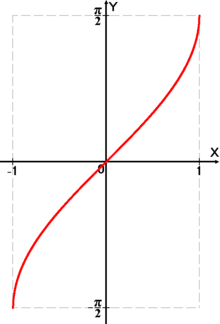
График функции .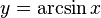

Арксинусом числа m называется такое значение угла x, для которого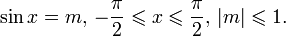

Функция 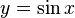непрерывна и ограничена на всей своей числовой прямой. Функция 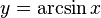является строго возрастающей.

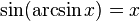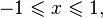
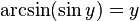· при

· при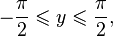

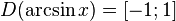· (область определения),

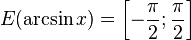· (область значений).

]Свойства функции arcsin

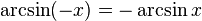· (функция является нечётной).

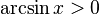· при .

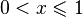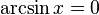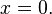
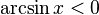· при

· при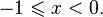

·

·

·

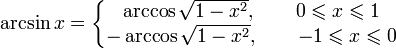
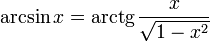
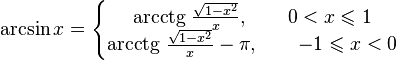
Функция arccos

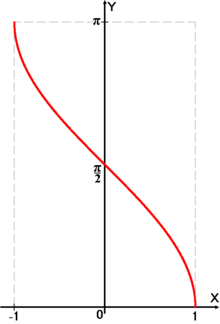
График функции .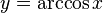

Арккосинусом числа m называется такое значение угла x, для которого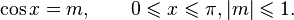

Функция 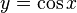непрерывна и ограничена на всей своей числовой прямой. Функция 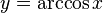является строго убывающей.

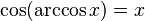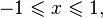
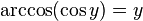· при

· при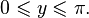

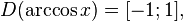· (область определения),

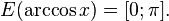· (область значений).

[править]Свойства функции arccos

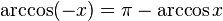· (функция центрально-симметрична относительно точки 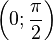), является индифферентной.

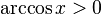· при

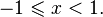
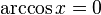· при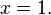

·

·

·

·

·

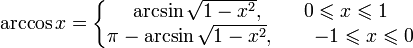
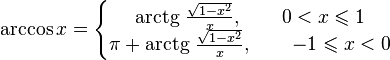
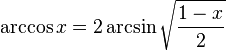
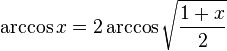
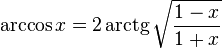
Функция arctg

График функции .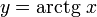

Арктангенсом числа m называется такое значение угла 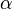, для которого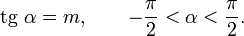

Функция 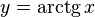непрерывна и ограничена на всей своей числовой прямой. Функция 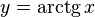является строго возрастающей.

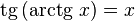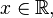
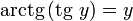· при

· при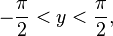

·

·

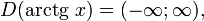
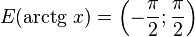
Свойства функции arctg

·

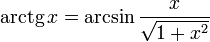
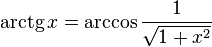· , при x > 0.

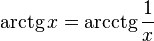· , при x > 0.

Функция arcctg

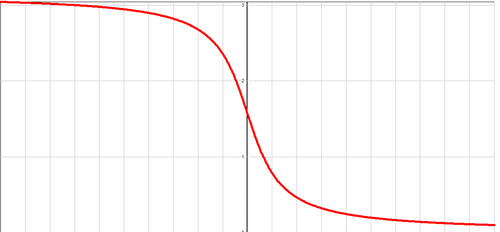
График функции y=arcctg x

Арккотангенсом числа m называется такое значение угла x, для которого

Функция 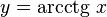непрерывна и ограничена на всей своей числовой прямой. Функция 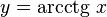является строго убывающей.

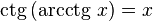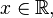
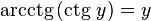· при

· при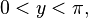

·

·

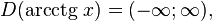
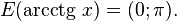
]Свойства функции arcctg

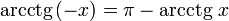· (график функции центрально-симметричен относительно точки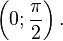

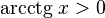· при любых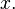

·

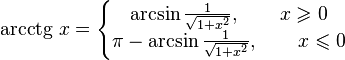
Билет №22. Гиперболические ф-и и их сво-ва.

Билет №23. Определение производной, ее геометрический и механический смысл. Ур-е касательной и нормали к гр ф-и. односторонние и бесконечные производные.

(Механический смысл производной)

Пусть задан путь 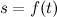движения материальной точки. Скорость данной материальной точки в момент времени 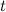есть производная от пути по времени :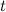

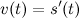
Односторонние производные

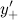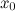Правой производной функции в данной точке называется величина:

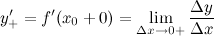
а левой производной - величина:

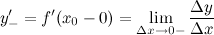
если эти пределы существуют.

Теорема: Для того чтобы в точке существовала производная 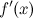, необходимо и достаточно, чтобы в точке функция имела правую и левую производные, и эти производные были равны между собой: .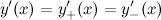

Определение: Если функция 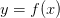, непрерывна в точке 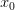и 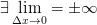, тогда производная 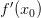называется бесконечной производной.

Билет №24. Дифференцируемость ф-и. связь м/у дифферен-тью и непрерывностью.

Билет №25. Производная суммы, произведения, частного ф-и.

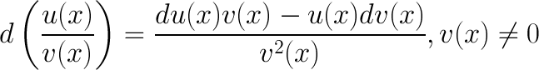
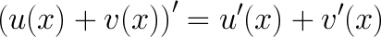
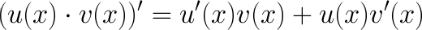
Билет №26. Производная степенной, показательной, логарифмической и тригонометрической функций.

Производная показательной функции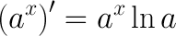

Производная степенной функции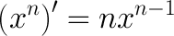

Производная логарифма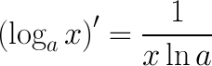

Производная тригонометрической функции:

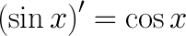
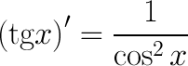
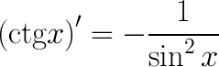
Билет №27.Производная обратной ф-и. Производные обратных тригонометрических фу-й.

Замечание

Дифференциал функции составляет основную часть ее приращения.

Замечание

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

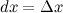
Замечание

Формулу для дифференциала функции можно записать в виде:

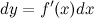
Отсюда получаем, что

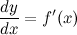
Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.

Производные высших порядков

Если функция имеет производную в каждой точке своей области определения, то ее производная 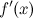есть функция от . Функция 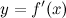, в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом 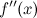. Таким образом

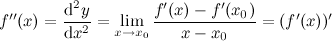
Формулировка теоремы Ферма

Теорема

Для любого натурального числа 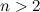уравнение

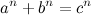
не имеет решений в целых ненулевых числах , 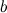и .

Теорема Ролля утверждает, что любая действительная дифференцируемая функция, принимающая одинаковые значения на концах интервала, должна иметь в этом интервале хотя бы одну стационарную точку, т.е. точку, в которой первая производная равна нулю. Геометрически это означает, что касательная к графику функции в этой точке горизонтальна

Вторая теорема Вейерштрасса
Если функция f(x) непрерывна на отрезке [a,b], то она достигает на нем своей точной верхней и нижней грани (т.е. наибольшего и наименьшего значения).

Теорема Ферма
Пусть функция f(x) определена в окрестности точки x0 и дифференцируема в этой точке. Тогда, если функция f(x) имеет локальный экстремум в точке x0, тоf′(x0)=0.Рассмотрим теперь теорему Ролля (или теорему о нуле производной) в более строгом изложении. Пусть функция y=f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и принимает одинаковые значения на концах данного отрезка:f(a)=f(b).Тогда на интервале (a,b) существует по крайней мере одна точка ξ∈(a,b), в которой производная функции f(x) равна нулю:f′(ξ)=0

.Доказательство.
Если функция f(x) постоянна на отрезке [a,b], то производная равна нулю в любой точке интервала (a,b),т.е. в этом случае утверждение справедливо.

Если функция f(x) не является постоянной на отрезке [a,b], то по теореме Вейерштрасса она достигает своего наибольшего или наименьшего значения в некоторой точке ξ интервала (a,b), т.е. в точке ξ существует локальный экстремум. Тогда по теореме Ферма производная в этой точке равна нулю:f′(ξ)=0.Теорема Ролля имеет наглядный физический смысл.Предположим, что тело движется вдоль прямой и через некоторый промежуток времени возвращается в исходную точку. Тогда в данном промежутке времени существует момент, в котором мгновенная скорость тела была равна нулю.

Теорема Ферма. (О равенстве нулю производной)

Пусть функция удовлетворяет следующим условиям:

1. она дифференцируема на интервале ;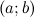

2. достигает наибольшего или наименьшего значения в точке .

Тогда производная в этой точке равна нулю, то есть .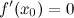

Следствие. (Геометрический смысл теоремы Ферма)

В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.

Теорема Ролля

Теорема

ТеоремаРолля. (О нуле производной функции, принимающей на концах отрезка равные значения)

Пусть функция

1. непрерывна на отрезке ;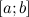

2. дифференцируема на интервале ;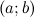

3. на концах отрезка 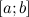принимает равные значения .

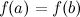Тогда на интервале 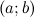найдется, по крайней мере, одна точка 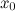, в которой .

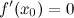Следствие. (Геометрический смысл теоремы Ролля)

Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.

Следствие.

Если 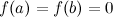, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.

Билет №35. Теоремы Коши и Лагранжа.

Теорема Лагранжа. (О конечных приращениях)

Пусть функция

1. непрерывна на отрезке ;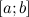

2. дифференцируема на интервале .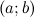

Тогда на интервале 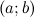найдется по крайней мере одна точка 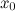, такая, что

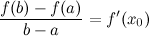
Замечание

Теорема Ролля есть частный случай теоремы Лагранжа, когда .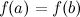

Следствие. (Геометрический смысл теоремы Лагранжа)

На кривой между точками и 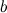найдется точка 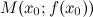, такая, что через эту точку можно провести касательную, параллельную хорде 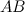(рис. 1).

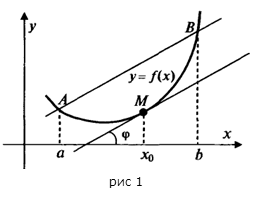
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:

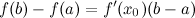
Теорема Коши

Теорема

Теорема Коши. (Об отношении конечных приращений двух функций)

Если функции и :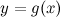

1. непрерывны на отрезке ;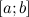

2. дифференцируемы на интервале ;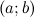

3. производная 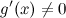на интервале ,

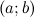тогда на этом интервале найдется по крайней мере одна точка 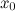, такая, что

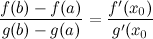
Теорема

Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке.

Теорема

Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое.

Билет №36. Раскрытие неопределенностей. Правило Лопиталя.

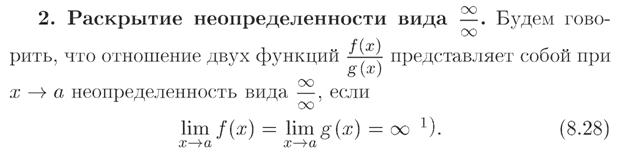
(Правило Лопиталя).

Пусть функции и 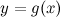удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки , кроме, может быть, самой точки ;

2) 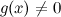и 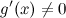в этой окрестности;

3) ;

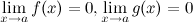4) 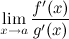существует конечный или бесконечный.

Тогда существует и 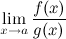, причем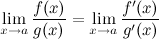

Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций.

Замечание

Правило Лопиталя распространяется на случай неопределенности типа 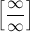при .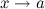

Замечание

Правило Лопиталя распространяется и на случай 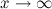. Чтобы убедится в этом, достаточно сделать замену 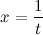и воспользоваться результатом выше приведенной теоремы.

Замечание

Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми.

Замечание

Хотя правило Лопиталя работает только с неопределенностям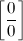и и 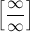, неопределенности других типов могут быть раскрыты с его помощью, если путем преобразований удастся привести изучаемую неопределенность к указанному типу.

Билет №37. Монотонность ф-и. условие монотонности ф-и.

Функция называется строго возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.

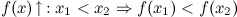
Функция 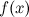называется строго убывающей на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.

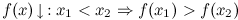
Функция строго возрастающая или строго убывающая на промежутке называется монотонной на этом промежутке.

Определение

Функция называется неубывающей на промежутке, если из неравенства 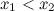следует неравенство .

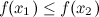Функция называется невозрастающей на промежутке, если из неравенства 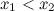следует неравенство .

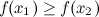Замечание

Обратное утверждение формулируется несколько иначе. Если функция возрастает на промежутке, то 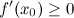или не существует.

Билет №38. Экстремум ф-и. необходимое и достаточное условие экстремума.

Точка 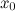называется точкой локального максимума функции 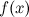, если существует такая окрестность этой точки, что для всех из этой окрестности выполняется неравенство: .

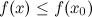Точка 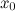называется точкой локального минимума функции 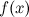, если существует такая окрестность этой точки, что для всех из этой окрестности .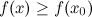

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума -локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка 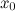называется точкой строгого локального максимума функции , если для всех из окрестности этой точки будет справедливо строгое неравенство .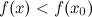

Точка 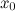называется точкой строгого локального минимума функции , если для всех из окрестности этой точки будет справедливо строгое неравенство .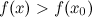

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Замечание

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Теорема

(Необходимое условие экстремума)

Если функция имеет экстремум в точке 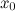, то ее производная 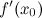либо равна нулю, либо не существует.

Точки, в которых производная равна нулю: 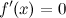, называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения 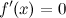), либо это точки, в которых производная 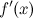не существует.

Замечание

Не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Теорема

(Первое достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. функция непрерывна в окрестности точки ;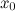

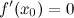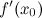2. или не существует;

3. производная 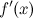при переходе через точку 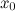меняет свой знак.

Тогда в точке 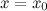функция имеет экстремум, причем это минимум, если при переходе через точку 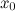производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку 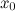производная меняет свой знак с плюса на минус.

Если производная 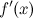при переходе через точку 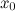не меняет знак, то экстремума в точке 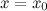нет.

Таким образом, для того чтобы исследовать функцию на экстремум, необходимо:

1. найти производную ;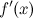

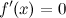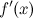2. найти критические точки, то есть такие значения , в которых или не существует;

3. исследовать знак производной слева и справа от каждой критической точки;

4. найти значение функции в экстремальных точках.

Теорема

(Второе достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. она непрерывна в окрестности точки ;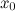

2. первая производная 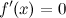в точке ;

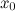3. 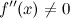в точке .

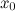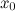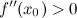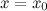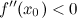Тогда в точке достигается экстремум, причем, если , то в точке функция имеет минимум; если , то в точке 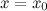функция достигает максимум.

Билет №39. Исследование ф-и на экстремум с помощью производной первого порядка и высших порядков.

Теорема

(Об условиях выпуклости или вогнутости графика функции)

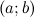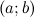Пусть функция определена на интервале и имеет непрерывную, не равную нулю в точке вторую производную. Тогда, если всюду на интервале , то функция имеет вогнутость на этом интервале, если , то функция имеет выпуклость.

Определение

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

(О необходимом условии существования точки перегиба)

Если функция имеет перегиб в точке , то или не существует.

Теорема

(О достаточном условии существования точки перегиба)

Если:

1. первая производная 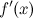непрерывна в окрестности точки ;