Железобетонной плиты в случае симметричного армирования

Однако использовать изгибные жесткости (22.15), (22.16) для анализа пластин можно только в случае цилиндрического изгиба, т.к. высоты 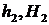могут быть неодинаковы. Кроме того, есть еще жесткость на кручение. Но если армирование симметрично относительно срединной плоскости, то нейтральные линии, на которых 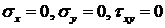будут лежать на этой срединной плоскости. Тогда .

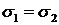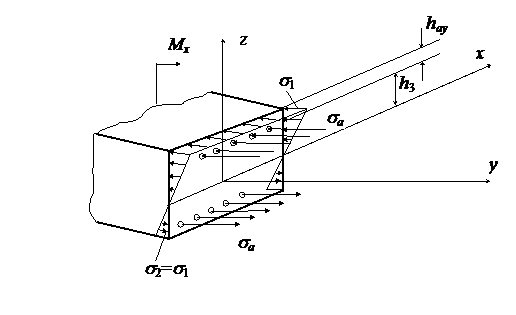
Рис.23.1

Снова рассмотрим левую часть балки или плиты. Условие ее равновесия имеют вид (далее учтено, что ):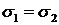

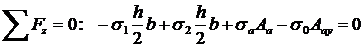(23.1)

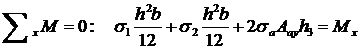(23.2)

Поскольку

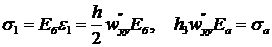(23.3)

То из (23.2) получим:

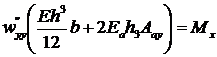(23.4)

Учитывая, что

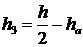
Получим

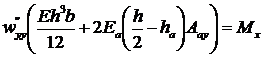(23.5)

Скобка при 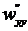называется для балки изгибной жесткостью в плоскости ZY. Обозначим ее через :

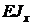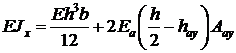(23.6)

Аналогично получим изгибную жесткость в плоскости ZX:

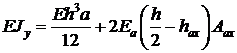(23.7)

Здесь 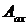- суммарная площадь арматуры, уложенной в направлении оси х, а 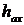- толщина защитного слоя этой арматуры.

Для пластин вместо изгибной жесткости вводят понятие цилиндрическая жесткость. Она представляет собой погонную жесткость и может быть получена по формулам:

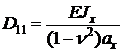(23.8)

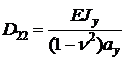(23.9)

Здесь 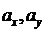размеры пластины вдоль осей х, у соответственно.

Если продольная и поперечная арматуры не сварены между собой, то крутильная жесткость для плиты определяется как обычно:

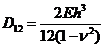(23.10)

Уравнение равновесия элемента пластины принимает вид, аналогичный уравнению Софи-Жермен:

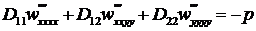(23.11)

Ясно, что в случае шарнирного опирания оно решается тем же методом, что и для изотропной пластины, т.е. перемещение может быть представлено в виде:

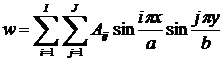. (23.12)

Коэффициенты 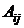определятся методом Бубнова-Галеркина.
24. ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ АРМИРОВАННЫХ ПЛАСТИН

Рассмотрим предельное состояние элемента железобетонной балки или пластины. В этом случае обычно считают, что в растянутой зоне напряжения вызывают растрескивание бетона. Поэтому там напряжениями пренебрегают.

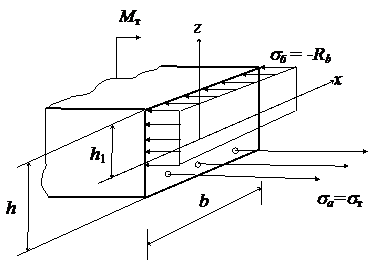
Рис.24.1

Рассмотрим левую часть балки (см.рис.24.1)

В сжатой зоне бетона напряжения считаются постоянными и равными предельному значению 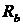. Напряжения в арматуре полагают равными пределу текучести:

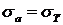(24.1)

Высоту сжатой зоны 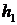найдем из условия равновесия левой части балки:

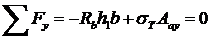(24.2)

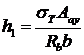(24.3)

Из второго уравнения равновесия найдем предельный момент М_т:

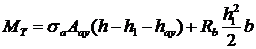(24.4)

Здесь - толщина защитного слоя.

В случае пластины используют погонный предельный момент:

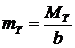(24.5)

Рассмотрим случай армирования под некоторым углом a к оси у:

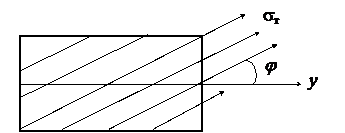
Рис.24.2

Тогда при проектировании на ось у вклад напряжений в арматуре будет меньше. Вместо (24.2) получим

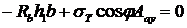(24.6)

Отсюда

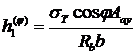(24.7)

Выражение для 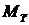также изменится:

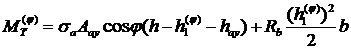(24.8)

Рис.24.3

В случае армирования сеткой (рис.24.3) вместо (24.6) получим

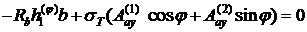(24.9)

Следовательно высота сжатой зоны бетона будет

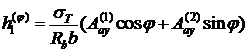(24.10)

Выражения для 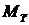при изгибе около оси Х получим из соотношения

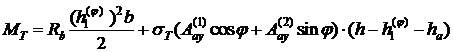(24.11)

Здесь 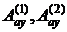- суммарная площадь арматуры в направлениях 1 и 2 соответственно. Можно показать, что для квадратной сетки

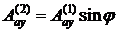(24.12)

25. ВЫЧИСЛЕНИЕ ПРЕДЕЛЬНОЙ НАГРУЗКИ ДЛЯ ПЛАСТИН

КИНЕМАТИЧЕСКИМ МЕТОДОМ

Рассмотрим простейший случай нагружения постоянной нагрузкой р. Эксперименты и расчеты показывают, что разрушение происходит по линиям, изображенным на рис.25.1.

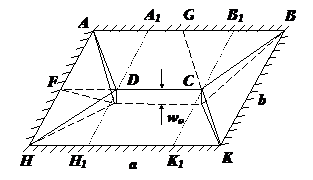
Рис.25.1

Пусть известен погонный предельный момент 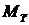. Для оценки 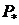сверху надо задать поле перемещений. Для простоты будем считать, что ÐВСК = 90°. Пусть перемещение w=1, тогда угол излома на линии DС легко вычисляется (см.рис.25.2).

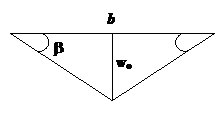
Рис.25.2

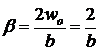(25.1)

Следовательно, работа изгибающего момента 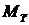будет

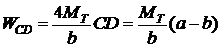(25.2)

Аналогично вычисляется работа на линии излома СК (см.рис.25.3). Тогда

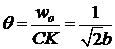(25.3)

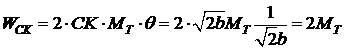(25.4)

На линии излома АВ угол излома равен b. Поэтому

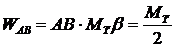(25.5)

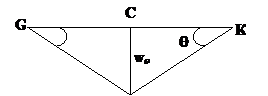Рис.25.3

На линии АН угол излома будет

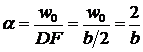(25.6)

Следовательно,

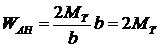(25.7)

Суммируя работу на всех линиях излома получаем работу изгибающего момента :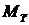

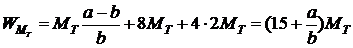(25.8)

Чтобы найти работу нагрузки 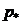учтем, что перемещения изменяются линейно по линиям координат. Тогда получим, что она равна объему, образующемуся под плоскостью АВКН, умноженному на :

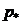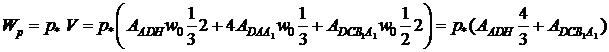(25.9)

Здесь 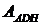- площадь треугольника ADH, 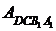- площадь прямоугольника DCB₁A₁ (см.рис.25.1). Выразим их через a,b:

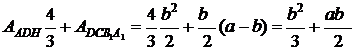
Приравнивая работы 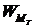и 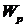и учитывая, что 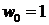, получим значение 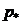в виде: 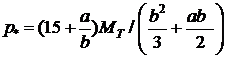(25.10)

Сравним со случаем замены давления нагрузки сосредоточенной силой Р = р А_АВКН. Тогда точное решение дает

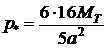
Приближенное решение дает 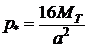, т.е. на 20% меньше.

Список литературы

1. Тимошенко С.П., Гудьер Дж. Теория упругости. – М.: Наука, 1975. – 576 с.
2. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности. - М.: «Высшая школа», 1984. – 472 с.
3. Работнов Ю.Н. Механика деформируемого твердого тела. - М.: «Наука», 1979. – 744 с.
4. Зубчанинов В.Г. Основы теории упругости и пластичности. – М.: Высшая школа, 1990. – 368 с.
5. Александров А.В. Потапов В.Д. Основы теории упругости и пластичности.- М.: Высшая школа, 1990.- 400 с.
6. Самуль В.И. Основы теории упругости и пластичности. – М.: Высшая школа, 1982. – 264 с.
7. Саргасян А.Е. Сопротивление материалов, теория упругости и пластичности. - М.: «Высшая школа», 2002.-286 с.
8. Кац А.М. Теория упругости. - СПб.: Лань, 2002. – 208 с.
9. Елисеев В.В. Механика упругих тел. - СПб.: Изд-во СПбГПУ, 2003. - 336 с.
10. Безухов Н.И. Основы теории упругости, пластичности и ползучести. – М.: Высшая школа, 1986. – 512 с.
11. Горшков А.Г., Старовойтов Э.И., Тарлаковский Д.В. Теория упругости и пластичности. – М.: Издательство «Физматлит», 2002 –416 с.
12. Кожаринова Л.В. Основы теории упругости и пластичности: учебное пособие для студентов строительных специальностей. - Орел: ОрелГТУ, 2009. - 85 с.
13. Барашков В.Н., Смолина И.Ю., Путеева Л.Е., Песцов Д.Н.. Основы теории упругости. – Томск : Изд-во Том. гос. архит.-строит. ун-та, 2011. – 184 с.

Содержание

	Введение................................................................................................
1.		Уравнения равновесия.........................................................................
	1.1.	Уравнения равновесия внутреннего малого элемента......................
	1.2.	Уравнения равновесия граничного элемента.....................................
	1.3.	Типы плоских задач теории упругости..............................................
2.		Кинематические соотношения ...........................................................
	2.1.	Соотношения Коши.............................................................................
	2.2	Следствие из соотношений Коши - условие совместности деформаций...........................................................................................
3.		Решения уравнений теории упругости в напряжениях.....................
	3.1.	Задача о дамбе.......................................................................................
	3.2.	Функция напряжений (функция Эри).................................................
4.		Некоторые методы приближенного решения задач теории упругости. Метод коллокаций.............................................................
5.		Метод Бубнова-Галеркина...................................................................
6.		Метод Рэлея-Ритца...............................................................................
7.		Метод конечных разностей.................................................................
8.		Метод конечных элементов.................................................................
9.		Теорема о минимуме потенциальной энергии упругой системы и ее применение для опосредованной оценки точности решения.....
10.		Задача Фламана.....................................................................................
11.		Осесимметричные задачи теории упругости.....................................
12.		Задача Кирша........................................................................................
13.		Задачи термоупругости........................................................................
14.		Теория изгиба жестких плит................................................................
	10.1.	Гипотезы Кирхгоффа-Лява..................................................................
	10.2.	Уравнение Софии-Жермен (уравнение для прогиба).............
	10.3.	Условия на границах пластины...........................................................
	10.4.	Точные решения задачи об изгибе жестких пластин........................
		1. Решение об изгибе защемленной эллиптической пластины........
		2. Задача о свободно опертой прямоугольной пластине под синусоидальной нагрузкой..................................................................
	10.5.	Решение задачи изгиба свободно опертой по краям пластины при произвольной нагрузке методом Бубнова-Галеркина.......................
	10.6.	Изгиб пластины под действием сосредоточенных сил.....................
	10.7.	Пластина на упругом основании.........................................................
15.		Приближенное выражение для касательных напряжений и угла закрутки при чистом кручении тонкой пластины
		Устойчивость плоской формы изгиба тонких балок
		Устойчивость пластин
18.		Расчёт тонких оболочек.......................................................................
	18.1.	Расчёт куполов по безмоментной теории...........................................
	18.2.	Краевой эффект.....................................................................................
		Теория пологих оболочек
		Устойчивость цилиндрической панели
		Устойчивость замкнутой цилиндрической оболочки
		ВЫРАЖЕНИЕ ДЛЯ ИЗГИБНОЙ ЖЕСТКОСТИ ЖЕЛЕЗОБЕТОННОЙ ПЛИТЫ
		ВЫРАЖЕНИЕ ДЛЯ ИЗГИБНОЙ ЖЕСТКОСТИ ЖЕЛЕЗОБЕТОННОЙ ПЛИТЫ В СЛУЧАЕ СИММЕТРИЧНОГО АРМИРОВАНИЯ
		ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ АРМИРОВАННЫХ ПЛАСТИН
		ВЫЧИСЛЕНИЕ ПРЕДЕЛЬНОЙ НАГРУЗКИ ДЛЯ ПЛАСТИН КИНЕМАТИЧЕСКИМ МЕТОДОМ
	Список литературы...............................................................................
	Содержание...........................................................................................

Каюмов Рашит Абдулхакович

Основы теории упругости и элементы теории пластин и оболочек

Редактор

Корректор

Подписано в печать 22.11.15 Формат 60х84/16

Заказ № Печать ризографическая Усл.печ.л. 5

Тираж 90 Бумага офсетная №1 Уч.-изд.л. 5

Отпечатано в полиграфическом секторе

Издательства КГАСУ.

420043, г.Казань, ул.Зеленая, д.1