Определение и свойства сходящихся рядов

СОДЕРЖАНИЕ

Введение……………………………………………………………………….4

Тема 1. Определение и свойства сходящихся рядов. 5

Тема 2. Признаки сходимости рядов с неотрицательными членами. 14

Тема 3. Абсолютно и условно сходящиеся ряды.. 31

Тема 4. Сходимость функциональных рядов. 40

Тема 5. Степенные ряды.. 53

Тема 6. Ряд Тейлора. 66

Тема 7. Ряды Фурье. 84

Список литературы.. 95

Предметный указатель. 96

Введение.

Учебное пособие по курсу числовые и функциональные ряды, которое мы хотим представить читателям, является исправленным и дополненным по сравнению с более ранними изданиями. В этом учебном пособии в небольшом объеме содержится обширный материал. Использование этого материала предоставляет широкие возможности для совершенствования учебного процесса студентов различных специальностей и профилей бакалавриата и специалитета, которые реализуются в рамках современных ФГОС ВО. Так же, данное издание может быть использовано студентами старших курсов и аспирантов, в качестве справочного пособия для повышения уровня научных исследований, особенно в областях математического моделирования, численных методов и комплексов программ. Элементы теории сопровождаются примерами с подробными решениями. Представлено решение типового варианта контрольной работы. Приводятся варианты упражнений для самостоятельных занятий.

Учебное пособие направлено на более тщательное изучение разделов математического анализа, поэтому содержит дополнительный материал. Это пособие направлено в помощь студентам для более глубокого понимания и усвоения материала, а так же для успешной сдачи экзаменов. Учебное пособие охватывает следующие темы раздела “числовые и функциональные ряды”: определение и свойства сходящихся рядов, признаки сходимости рядов с неотрицательными членами, абсолютно и условно сходящиеся ряды, сходимость функциональных рядов, степенные ряды, ряд Тейлора и ряды Фурье.

Издание является логическим продолжением предыдущих изданий авторов, посвященных дифференциальному и интегральному исчислению функций одной и нескольких переменных, а также курса дифференциальных уравнений с элементами теории устойчивости.

Материал структурирован в виде семи тем, содержащих основные определения, теоремы и соответствующие примеры. Конец доказательств помечается знаком ■, начало решения примеров помечается знаком 3, конец решения – знаком 4.

Учебное пособие соответствует утвержденной программе курса высшей математики в технологическом университете и рекомендовано кафедрой «Прикладная математика» в качестве дополнительной литературы для изучения материала студентами первого и второго курса.

ЧИСЛОВЫЕ РЯДЫ

Задачи повышенной сложности

Исследовать на сходимость ряды:

93. 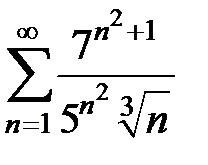.	94. .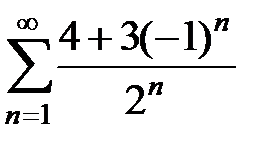
95. 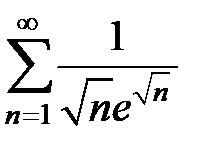.	96. .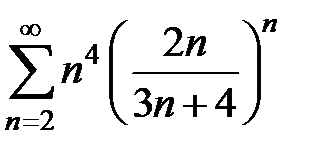
97. 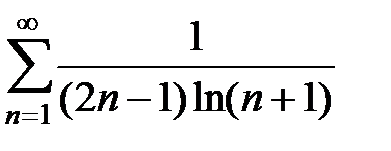.	98. .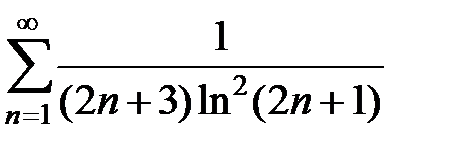
99. 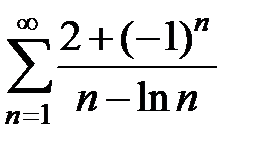.	100. .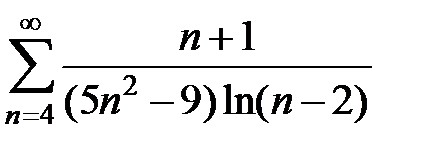
101. 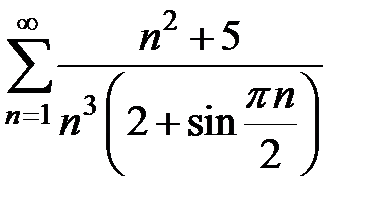.	102. .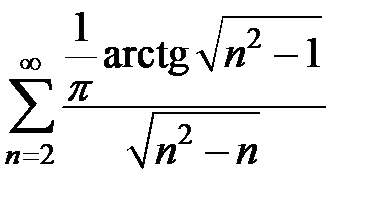
103. 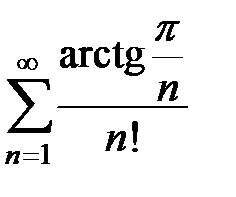.	104. .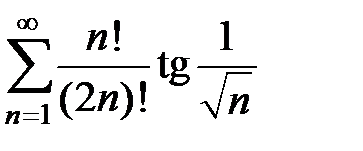
9.105. 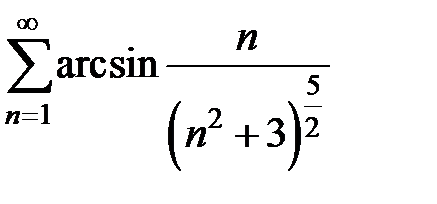.	9.106. .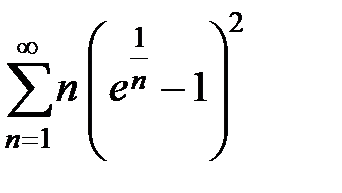

107. .

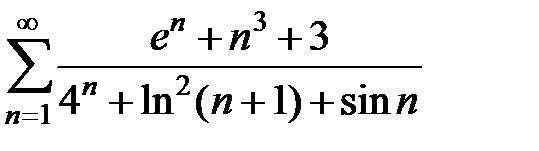108. .

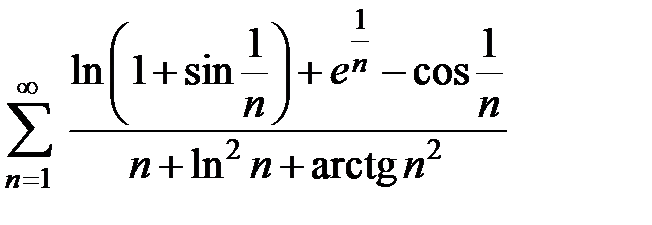109. Исследовать на сходимость ряд 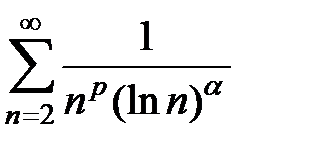при различных действительных значениях 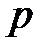и .

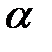110. Исследовать на сходимость ряд 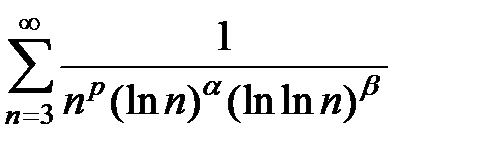при различных действительных значениях 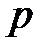, 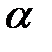и .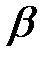

111. Положим 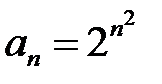. Доказать, что ряд 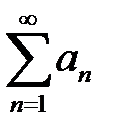расходится, а ряд 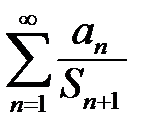сходится.

112. Доказать, что сумма ряда с неотрицательными членами не изменится при произвольной перестановке его членов.

Тема 3. Абсолютно и условно сходящиеся ряды

3.1. Абсолютно сходящиеся ряды

Рассмотрим теперь ряды с действительными членами произвольных знаков. Такие ряды называются знакопеременными.

Теорема(достаточное условие сходимости знакопеременного ряда). Пусть дан ряд с произвольными (действительными или комплексными) членами

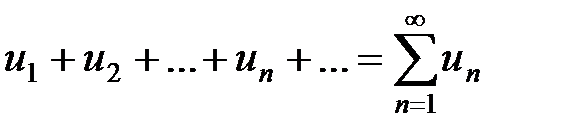. (15)

Если сходится ряд

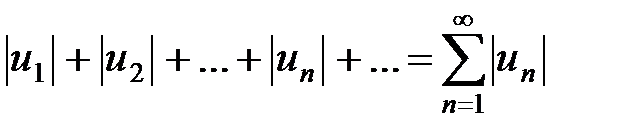, (16)

составленный из абсолютных величин членов данного ряда, то сходится и данный числовой ряд.

Доказательство.В силу необходимости выполнения условия Коши для сходимости ряда (см. п.1.4), для любого ε > 0 существует такой номер N(ε), что при любом n ≥ N(ε) и любом целом p ≥ 0 выполняется неравенство

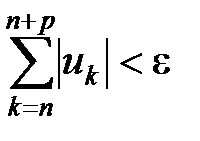. (17)

Поскольку

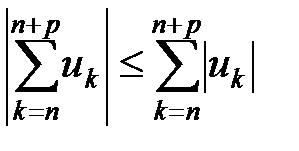
(в частности, для комплексных чисел это неравенство вытекает из неравенства треугольника[1]), то из (17) следует, что для всех номеров n ≥ N(ε) и всех целых p ≥ 0 выполняется неравенство

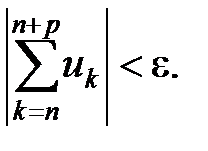
А это и означает в силу достаточности выполнения условия Коши для сходимости ряда, что ряд (15) сходится. ■

Мы доказали, что из условия сходимости ряда (16) вытекает сходимость ряда (15). Обратное утверждение, вообще говоря, неверно. Существуют знакопеременные ряды, которые сходятся, а ряды, составленные из абсолютных величин их членов, расходятся. Например, ряд 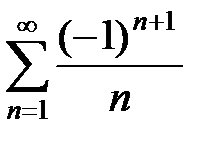сходится (это будет доказано в п.3.2), а ряд 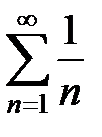, составленный из абсолютных величин его членов, расходится (гармонический ряд).

Определение.Ряд с произвольными (действительными или комплексными) членами 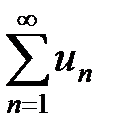, называют абсолютно сходящимся, если сходится действительный ряд 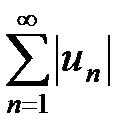из абсолютных величин его членов.

Используя данное определение доказанную выше теорему можно сформулировать так: Если ряд абсолютно сходится, то он сходится.

Пример 23. Исследовать на абсолютную сходимость ряд .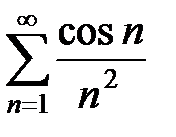

3Составим ряд из абсолютных величин членов исходного ряда:

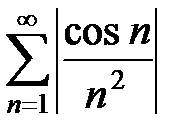. (19)

Так как при любом n имеет место соотношение 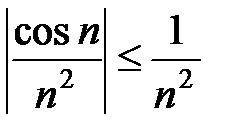, а ряд 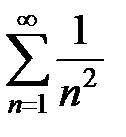сходится (ряд Дирихле, a = 2 > 1), то по признаку сравнения ряд (19) сходится. Следовательно, исходный ряд сходится абсолютно. 4

3.2. Знакочередующиеся ряды. Признак Лейбница

Определение. Знакочередующимся рядом называется ряд, у которого члены попеременно то положительны, то отрицательны, т.е. ряд такого вида:

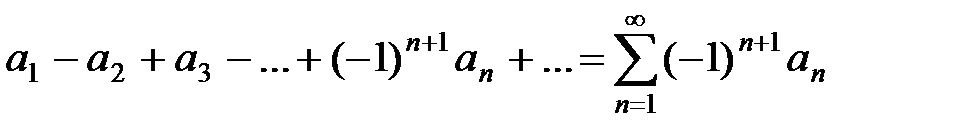, где a_n> 0, "n Î N. (20)

Для знакочередующихся рядов имеет место следующий достаточный признак сходимости:

Теорема (признак Лейбница).Пусть знакочередующийся ряд (20) удовлетворяет условиям:

1) a₁³ a₂³ a₃³…³ a_n³ a_n+1³…;

2) .

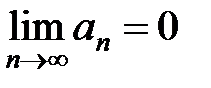Тогда этот знакочередующийся ряд сходится, его сумма неотрицательна и не превосходит первого члена.

Доказательство.Рассмотрим сначала частичную сумму четного числа членов ряда (20)

S_2n= a₁– a₂+ a₃– a₄+…+ a_2n–1– a_2n= (a₁– a₂) + (a₃– a₄) +…+ (a_2n–1– a_2n). Из первого условия теоремы следует, что выражение в каждой скобке неотрицательно. Значит, сумма S_2n≥ 0 и не убывает с возрастанием номера n. С другой стороны эту сумму можно записать так:

S_2n= a₁– (a₂– a₃) – (a₄– a₅) –…– (a_2n–2– a_2n–1) – a_2n .

Заметим, что S_2n≤ a₁. Таким образом, последовательность S₂, S₄, S₆,…, S_2n… не убывает и ограничена сверху. Следовательно, она имеет предел 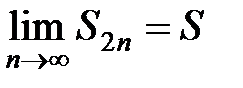, причем 0 ≤ S ≤ a₁.

Рассмотрим теперь частичные суммы нечетного числа членов ряда (20). Очевидно, что S_2n+1= S_2n+ a_2n+1. Отсюда следует, что

,

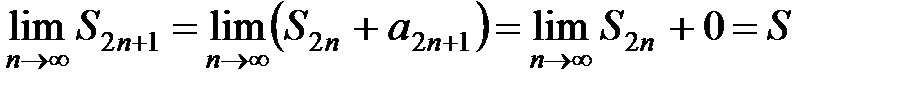так как 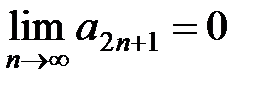по второму условию теоремы. Итак, 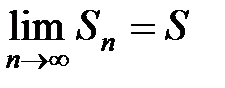как при четном, так и при нечетном n. Следовательно, ряд (20) сходится, причем 0 ≤ S ≤ a₁ . ■

Если знакочередующийся ряд 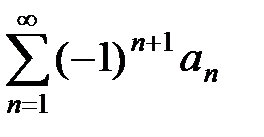, a_n> 0, n Î N, удовлетворяет условиям признака Лейбница, то модуль суммы всякого его остатка 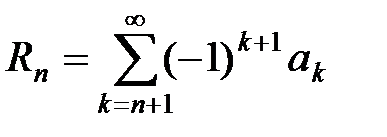оценивается сверху числом a_n+1: |R_n| £ a_n+1, n Î N. Для вычисления суммы такого ряда с заданной точностью d решаем неравенство a_{n +1} < d, откуда находим количество членов ряда, которое необходимо взять для вычисления суммы ряда с заданной точностью d. Далее вычисляем n-ю частичную сумму S » S_n= a₁ – a₂+…+(–1)^n–1a_n.

Пример 24. Исследовать на сходимость ряд .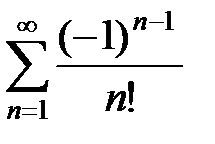

3Проверим условия признака Лейбница для данного знакочередующегося ряда с :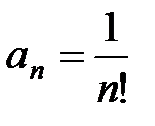

1) последовательность 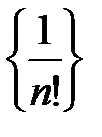убывает;

2) .

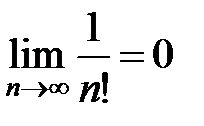Следовательно, по признаку Лейбница исходный ряд сходится.4

Пример 25. Вычислить сумму ряда 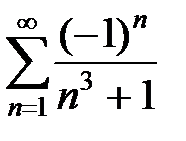с точностью до 0,01.

3Данный знакочередующийся ряд удовлетворяет условиям признака Лейбница:

1) Последовательность 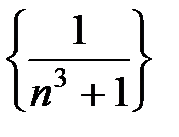убывает;

2)

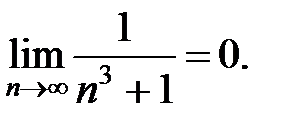
Следовательно, справедливо неравенство

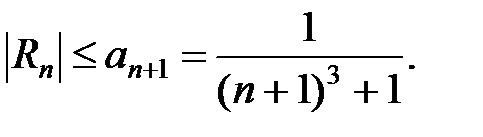
Если a_n+1 < δ, то и |R_n| < δ. Следовательно, достаточно найти минимальное число 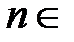N, для которого выполняется неравенство

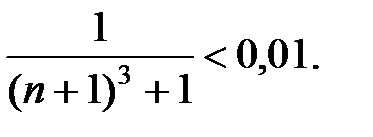
Преобразуем это неравенство: (n + 1)³+ 1>100, n > 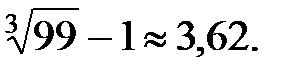В результате находим, что n = 4. Таким образом,

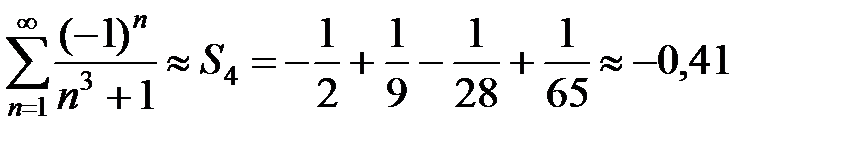
с точностью до 0,01. 4

3.3. Условно сходящиеся ряды

Определение. Ряд с произвольными (действительными или комплексными) членами 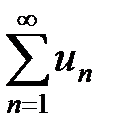называют условно сходящимся,если он сходится, но не является абсолютно сходящимся, т.е. если 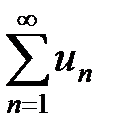сходится, а ряд 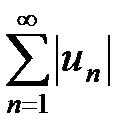расходится.

Заметим, что деление сходящихся рядов на абсолютно и условно сходящиеся весьма существенно. Например, для условно сходящихся рядов сумма ряда не равна сумме положительных и сумме отрицательных членов ряда, как это имеет место для абсолютно сходящихся рядов. В общем случае различие свойств таких рядов отражают следующие теоремы.

Теорема. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.

Теорема (Римана). Если ряд сходится условно, то какое бы мы ни задали значение А, конечное или равное ±¥, можно так переставить члены этого ряда, что его сумма будет в точности равной А.

Пример 26. Исследовать на абсолютную и условную сходимость ряд .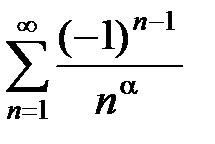

3Сначала изучим ряд 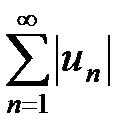. В нашем случае 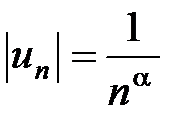. Если a £ 0, то 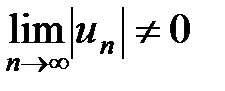и, значит, ряд 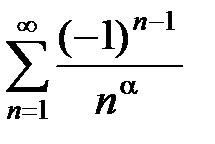расходится. При a > 0 возможны два варианта:

а) если a > 1, то ряд 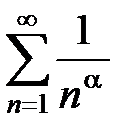сходится, откуда следует, что ряд 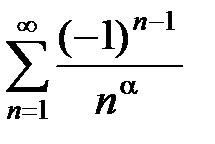сходится абсолютно;

б) если 0 < a £ 1, то ряд 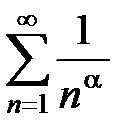расходится, значит, исходный ряд не будет сходиться абсолютно.

Исследуем ряд 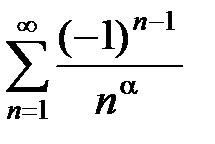на условную сходимость. Докажем, что этот ряд удовлетворяет признаку Лейбница.

Действительно, во-первых, последовательность 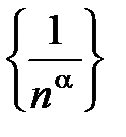убывает, во-вторых, 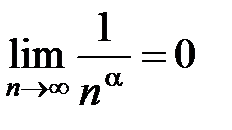. Согласно признаку Лейбница ряд сходится.

Таким образом, при a £ 0 ряд 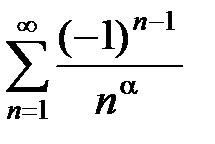расходится, при 0 < a £ 1 сходится условно, при a > 1 сходится абсолютно.4

Пример 27. Исследовать на абсолютную и условную сходимость ряд .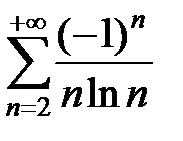

3Проверим, сходится ли ряд из модулей членов ряда, т.е. ряд 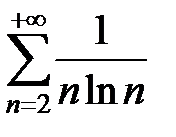. Функция 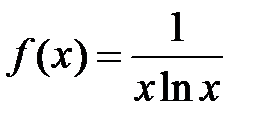удовлетворяет всем требованиям, наложенным на нее в интегральном признаке Коши,

.

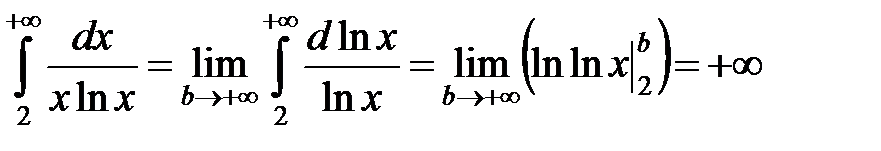Следовательно, ряд 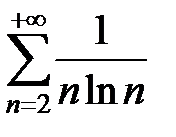расходится, т.е.ряд 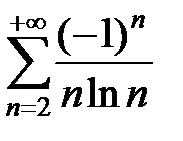не является абсолютно сходящимся.

Исследуем ряд 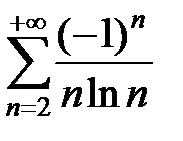на условную сходимость. Последовательность 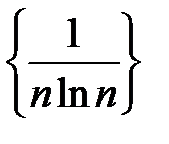убывает, 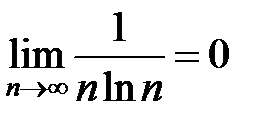. Следовательно, по признаку Лейбница ряд сходится. Значит, данный ряд сходится условно. 4

Пример 28. Исследовать на абсолютную и условную сходимость ряд 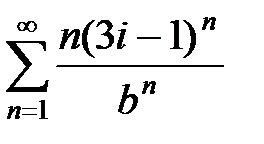, b Î R, b > 0.

3Исследуем этот ряд на абсолютную сходимость. Для выяснения сходимости ряда 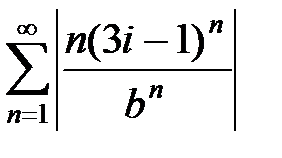воспользуемся признаком Даламбера. Обозначая 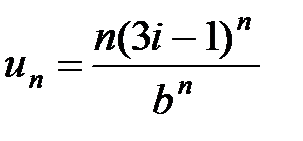, получаем , , .

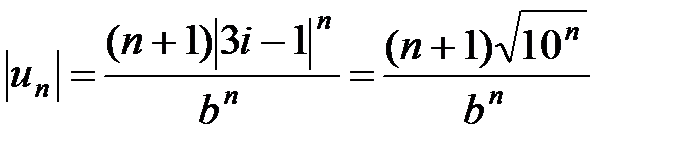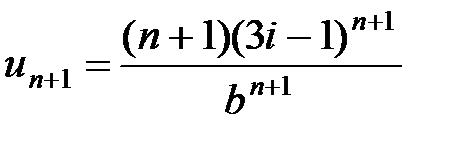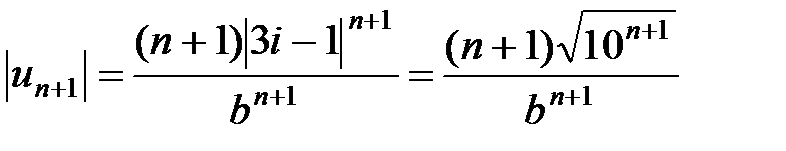Следовательно, .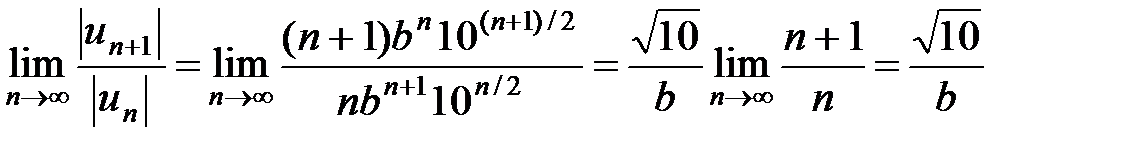

Таким образом, если 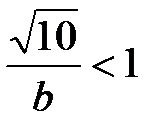, т.е. 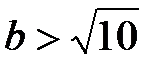, то ряд 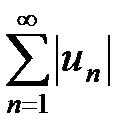сходится и, следовательно, исходный ряд сходится абсолютно. Если же 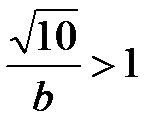, т.е. 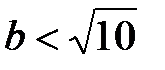, то ряд 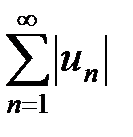расходится и, следовательно, исходный ряд не является абсолютно сходящимся. Более того, исходный ряд в этом случае расходится в силу невыполнения необходимого признака сходимости ряда.

При 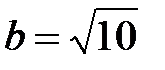признак Даламбера использовать нельзя. В этом случае |u_n| = n, и поскольку |u_n| не стремится к нулю при n ® ¥, то не выполняется необходимый признак сходимости как для ряда 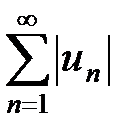, так и для ряда 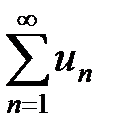. Следовательно, в этом случае исходный ряд расходится.4

Исследовать на абсолютную и условную сходимость следующие ряды:

147. 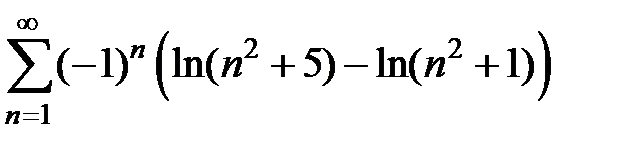.	148. .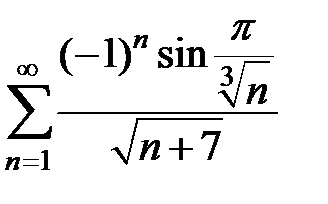
149. 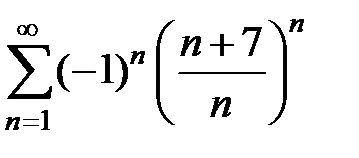.	150. .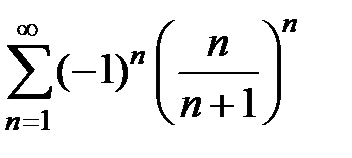
151. 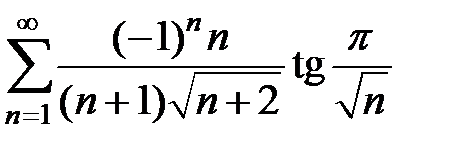.	152. .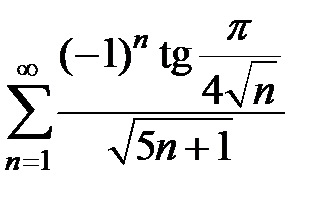
153. 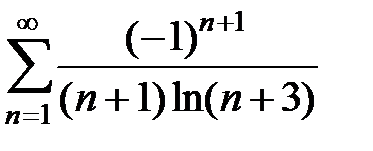.	154. .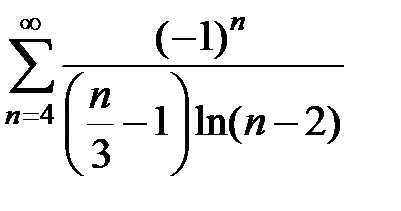
155. 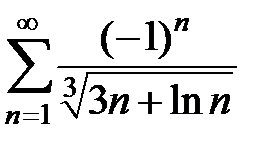.	156. .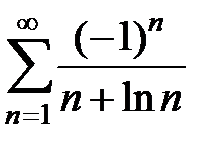
157. 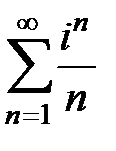.	158. .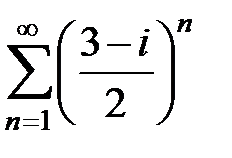
159. 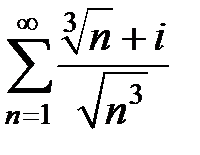.	160. .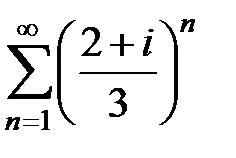

161. Доказать, что члены абсолютно сходящегося ряда можно переставлять произвольным образом; при этом сумма ряда не изменится.

162. Пусть ряд 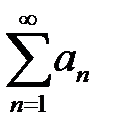сходится и 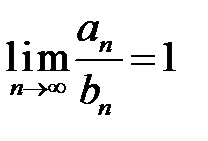. Можно ли утверждать, что сходится ряд ?

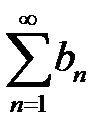Рассмотреть пример 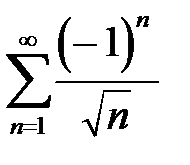и .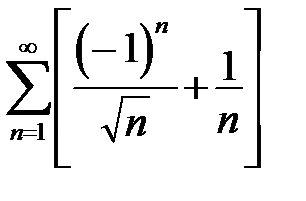

9.163. Показать, что сумма S условно сходящегося ряда 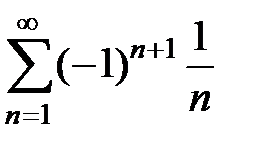уменьшится вдвое, если после каждого положительного члена ряда поместить два последующих отрицательных, и увеличится в полтора раза, если после двух положительных членов поместить один отрицательный.

164. Члены сходящегося ряда 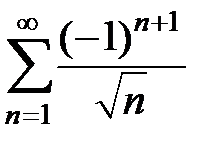переставить так, чтобы он стал расходиться.

ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Задачи повышенной сложности

Исследовать ряд на равномерную и абсолютную сходимость.

185. .

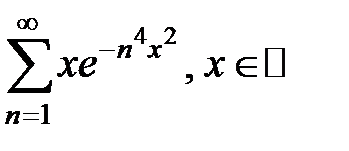186. .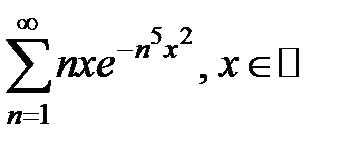

187. Доказать, что если члены равномерно сходящегося в области 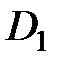функционального ряда 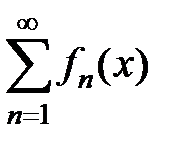умножить на одну и ту же ограниченную в области 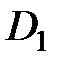функцию 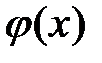, то равномерная сходимость ряда не нарушится.

188. Доказать, что если функции 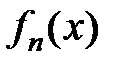непрерывны в области 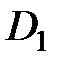и ряд 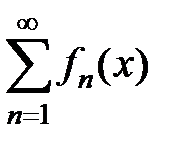равномерно сходится в этой области, то его сумма 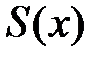непрерывна в области .

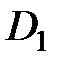189. Определить при 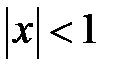сумму и остаток ряда 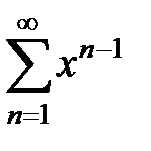и показать, что он сходится равномерно на отрезке 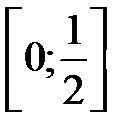. При каком 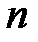остаток 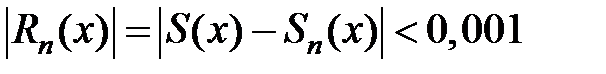для любого 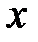на этом отрезке?

190. Показать, что ряд 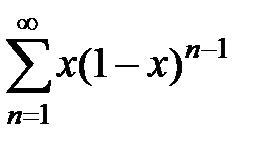сходится неравномерно на отрезке 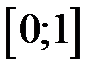и равномерно на отрезке 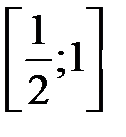. При каком 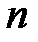остаток 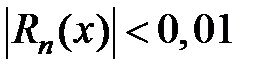для любого 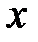на отрезке ?

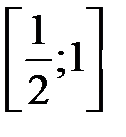191. Показать, что ряд 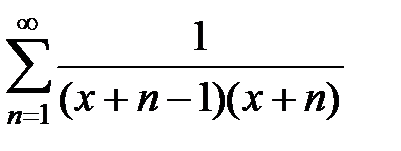сходится равномерно к 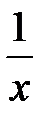в интервале 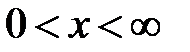. При каком 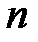(и любом 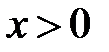) остаток ряда ?

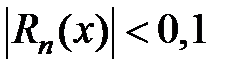192. Показать, что ряд 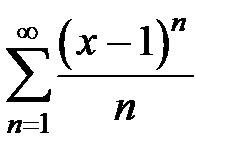сходится равномерно на отрезке 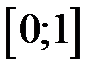. При каких 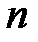и любом 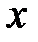на этом отрезке ?

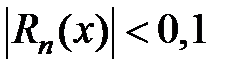Тема 5. Степенные ряды

5.1. Основные понятия. Теорема Абеля

Определение.Функциональный ряд вида

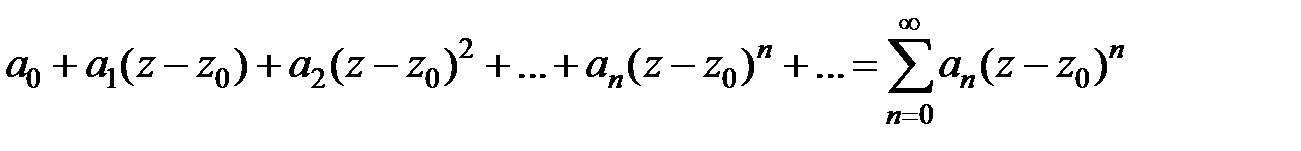, (9)

где a_n, z, z₀Î C, называется степенным рядом по степеням (z – z₀) Числа a_n, n = 0, 1, 2,… называются коэффициентами степенного ряда, z₀– центром степенного ряда.

В частности, ряд

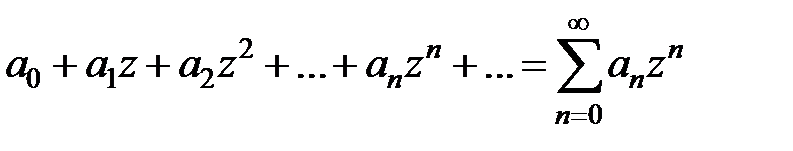(10)

является степенным по степеням z. С помощью замены z – z₀= Z ряд (9) сводится к ряду (10).

Придавая z различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений z, при которых ряд (10) сходится, называется областью сходимости степенного ряда. Это множество всегда не пусто, так как любой степенной ряд (10) сходится при z = 0.

Теорема 1 (Абеля).Если степенной ряд (10) сходится в точке z = z₁¹ 0, то он абсолютно сходится для всех z таких, что |z| < |z₁|. Если же ряд (10) расходится в точке z = z₂ ¹ 0, то он расходится и для всех z таких, что |z| > |z₂|.

0

|z1|

z1

K1

Доказательство. а) Пусть K₁= {z: |z| < |z₁|} – круг на комплексной плоскости с центром в точке О радиуса |z₁|, как изображено на рисунке, и пусть z – произвольная точка круга K₁, т.е. |z| < |z₁|, и поэтому

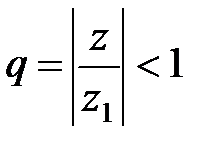. (11)

Так как ряд (10) по условию сходится в точке z₁, то должно выполняться условие 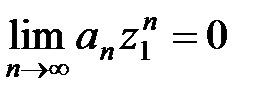, откуда следует, что последовательность 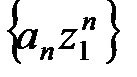ограничена, т.е. существует число М > 0 такое, что

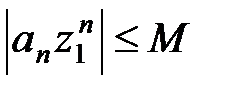, n = 0, 1, 2,… (12)

Используя неравенства (11) и (12), получаем:

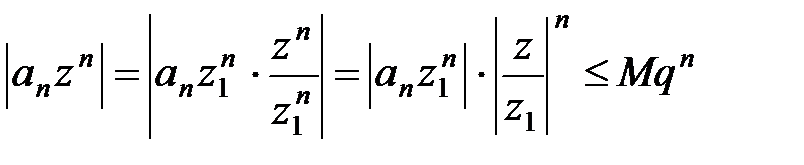, где 0 £ q < 1. (13)

Так как ряд 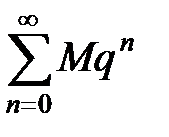, составленный из членов геометрической прогрессии со знаменателем 0 £ q < 1, сходится, то по признаку сравнения сходится и ряд 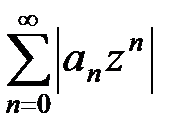, т.е. ряд (10) сходится абсолютно в каждой точке круга K₁.

б) Пусть теперь ряд (10) расходится в точке z₂ ¹ 0. Требуется показать, что он расходится для всех z, удовлетворяющих условию |z| > |z₂|. Предположим обратное, т.е. допустим, что при некотором значении z, таком, что |z| > |z₂|, ряд (10) сходится. Тогда по только что доказанной первой части теоремы ряд (10) должен сходиться и в точке z₂. Но это противоречит тому, что в точке z₂ряд расходится. ■

5.2. Радиус и круг сходимости степенного ряда

Теорема 2.Для всякого степенного ряда (10) справедливо одно из следующих утверждений:

1) существует число R > 0, такое, что при всех z, таких, что |z| < R , ряд сходится абсолютно, а при |z| > R – расходится;

2) ряд сходится только в точке z = 0;

3) ряд сходится для всех z.

Поясним эту теорему. Пусть D – множество всех точек сходимости ряда (10). Это непустое множество, т.к. в точке z = 0 ряд (10) сходится.

Если D – неограниченное множество, то ряд (10) сходится в произвольной точке z комплексной плоскости. В самом деле, возьмем точку z₁Î D, такую, что |z| < |z₁|. Тогда по теореме Абеля ряд (10) будет сходиться в точке z (третье утверждение).

Пусть D – ограниченное множество. Может оказаться, что множество D состоит из одной точки z = 0. Тогда ряд (10) сходится только в точке z = 0 и расходится при z ¹ 0 (второе утверждение).

абс. сходится

z1

z2

R

расходится

Пусть теперь D содержит точку z₁ ¹ 0. Тогда по теореме Абеля ряд (10) будет сходиться для всех z, таких, что |z| < |z₁|. Если z₂Ï D, | z₂| > |z₁|, то ряд (10) будет расходиться для всех z, таких, что |z| > |z₂|. Тогда существует число R: |z₁| < R < |z₂|, такое, что окружность |z| = R (на рисунке обозначена пунктиром) отделяет область сходимости от области расходимости, т.е. ряд сходится для всех z, таких, что |z| < R и расходится для всех z, таких, что |z| > R (первое утверждение).

Вопрос о сходимости ряда (10) в точках окружности |z| = R, R > 0 остается открытым и решается отдельно для каждого ряда.

Определение. Пусть задан степенной ряд 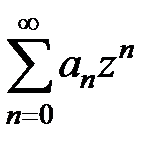. Если R – неотрицательное число или +¥, обладает тем свойством, что при всех z, для которых |z| < R, этот ряд сходится, а при всех z, для которых |z| > R – расходится, то оно называется радиусом сходимости степенного ряда. Множество точек z, для которых |z| < R, называется – кругом сходимости ряда (в случае ряда с действительными членами интервал (–R, R) – интервалом сходимости).

Так, в доказанной выше теореме в случае 2) полагают радиус сходимости R = 0, в случае 3) R = +¥.

Теорема 3. Если существует конечный или бесконечный 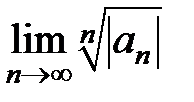, то для радиуса R сходимости ряда (10) справедлива формула

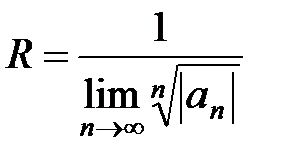, (14)

а если существует конечный или бесконечный 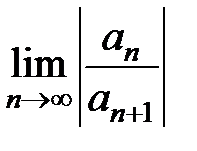, то

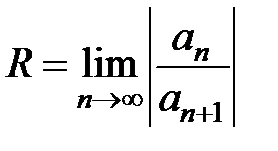. (15)

Доказательство. 1) Докажем сначала формулу (14). Обозначим .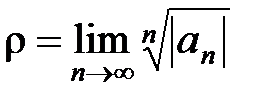

а) Пусть 0 < r < +¥ и пусть z₁– произвольная точка круга 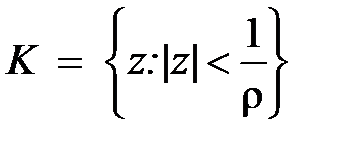, тогда 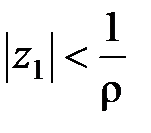. Рассмотрим предел

.

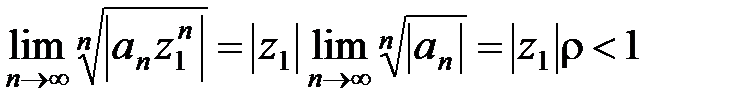По признаку Коши (см. п.2.3) ряд 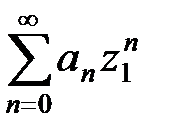абсолютно сходится. Так как точка z₁– произвольная точка круга K, то ряд (10) абсолютно сходится в этом круге.

Пусть точка z₂лежит вне круга K, тогда 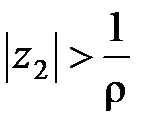и поэтому

.

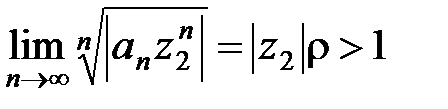Следовательно, ряд 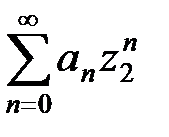расходится при .

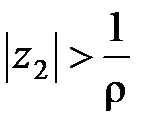Если правая часть равенства (14) положительное число, то ряд (10) сходится в круге Kи расходится вне этого круга. Значит, 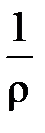– радиус сходимости ряда (10).

б) Если r= 0, то 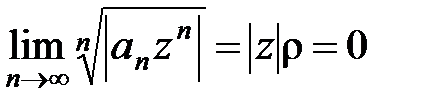для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (14) верна и в этом случае.

в) Если r = +¥, то для любой точки z ¹ 0 имеем 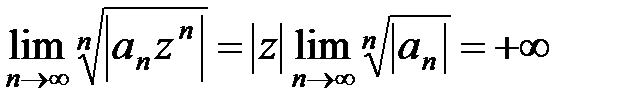и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.

Таким образом, величина 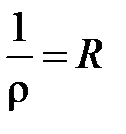– радиус сходимости степенного ряда (10).

2) Теперь докажем формулу (15). Доказательство аналогично первому случаю. Обозначим .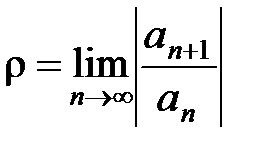

а) Пусть 0 < r < +¥ и пусть z₁– произвольная точка круга 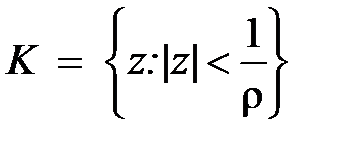, тогда 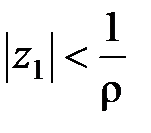. Рассмотрим предел

.

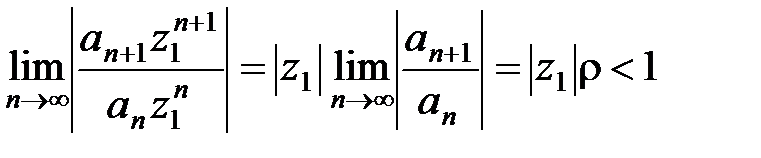По признаку Даламбера (см. п.2.2) ряд 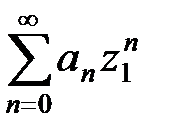абсолютно сходится. Так как точка z₁– произвольная точка круга K, то ряд (10) абсолютно сходится в этом круге.

Пусть точка z₂лежит вне круга K, тогда 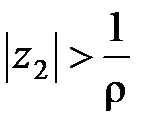и поэтому

.

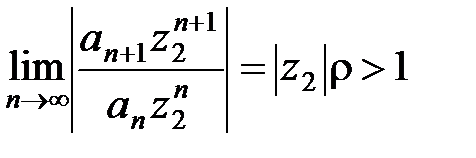Следовательно, ряд 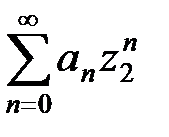расходится при .

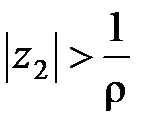Если правая часть равенства (15) положительное число, то ряд (10) сходится в круге Kи расходится вне этого круга. Значит, 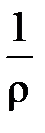– радиус сходимости ряда (10).

б) Если r= 0, то 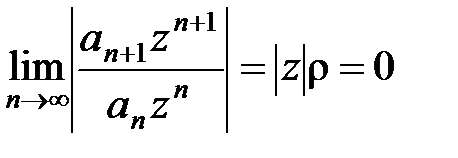для любой точки z комплексной плоскости, и поэтому ряд (10) сходится при любом z. Это означает, что радиус сходимости ряда R = +¥ и формула (15) верна и в этом случае.

в) Если r = +¥, то для любой точки z ¹ 0 имеем 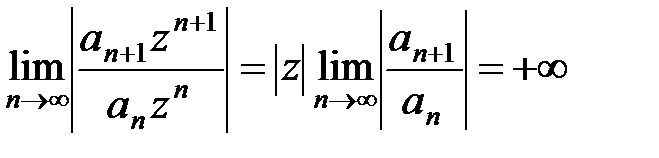и поэтому ряд (10) при z ¹ 0 расходится. Это означает, что R = 0.

Таким образом, величина 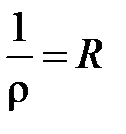– радиус сходимости степенного ряда (10). ■

Если пределы 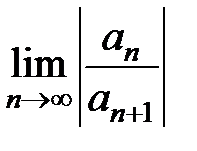и 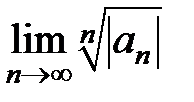для степенного ряда 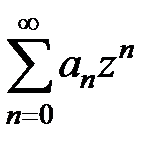не существуют (как, например, для рядов только с четными или нечетными степенями z), то формулы (14) и (15) применять нельзя. Однако непосредственное использование признаков Даламбера и Коши для рядов 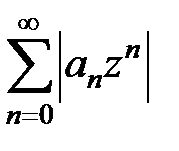часто позволяет определить радиус круга сходимости.

Все сказанное с помощью преобразования типа Z = z – z₀ (z – новая переменная, z₀ – фиксировано) переносится и на степенные ряды по степеням (z – z₀) вида (9). Областью сходимости такого ряда является круг вида |z – z₀| < R с точностью до его граничных точек. Этот круг называется кругом сходимости ряда (9), а R – его радиусом сходимости.

Областью сходимости степенного ряда с действительными членами

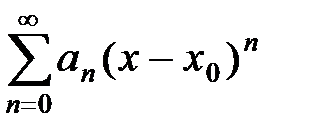
может оказаться либо интервал (x₀ – R, x₀ + R), либо отрезок [x₀ – R, x₀ + R], либо один из полуинтервалов (x₀ – R, x₀ + R] или [x₀ – R, x₀ + R). Если 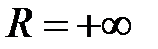, то областью сходимости будет вся числовая ось, т.е. интервал 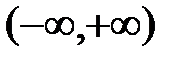, если R = 0, то область сходимости будет состоять из одной точки x₀.

Для отыскания области сходимости степенного ряда

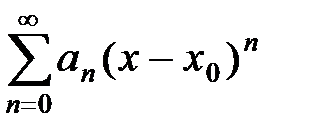
нужно сначала вычислить его радиус сходимости R (например, по одной из формул (14), (15)) и тем самым найти интервал сходимости (x₀ – R, x₀ + R), в котором ряд абсолютно сходится, затем исследовать сходимость ряда в концах интервала сходимости – в точках x = x₀ – R, x = x₀ + R.

Пример 6. Найти радиус сходимости и область сходимости ряда .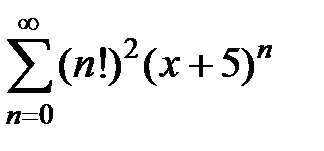

3Выпишем x₀= –5 и коэффициенты ряда a_n= (n!)². Существует 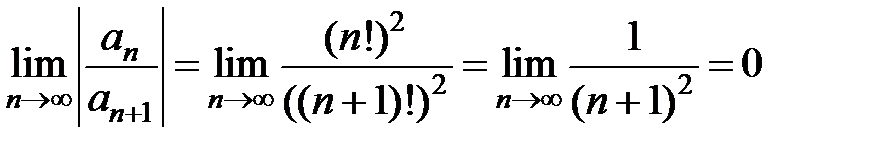. Таким образом, радиус сходимости R = 0, область сходимость состоит из единственной точки x = –5.4

Пример 7. Найти радиус сходимости и область сходимости ряда 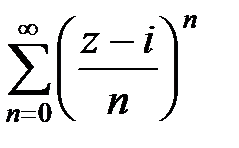, z Î C.

3Заметим, что z₀= i и 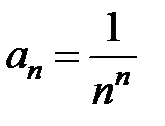. Использую формулу (12), находим радиус сходимости ряда 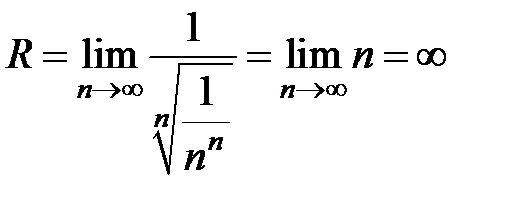. Таким образом, R = ¥. Это означает, что ряд сходится всюду на комплексной плоскости C.4

Пример 8. Найти радиус, интервал и область сходимости ряда .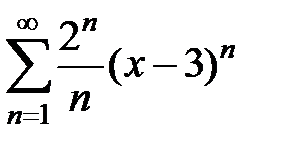

3Выпишем x₀= 3 и коэффициенты ряда 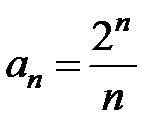. Найдем 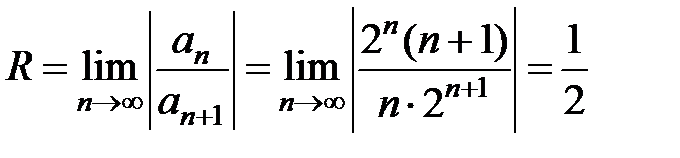. Концы интервала сходимост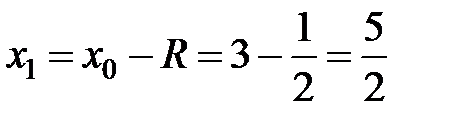и и .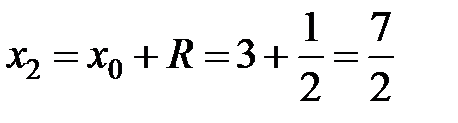

Итак, ряд абсолютно сходится для всех x из интервала .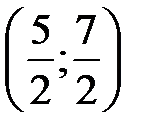

Исследуем поведение ряда на концах интервала сходимости. Подставляем в заданный ряд 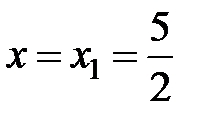. Получится числовой ряд 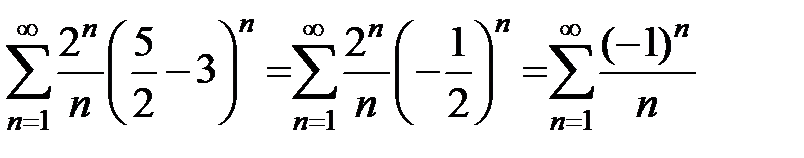. Этот знакочередующийся ряд удовлетворяет условиям признака Лейбница, следовательно, он сходится.

Подставим в заданный ряд 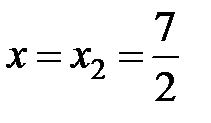. Получим 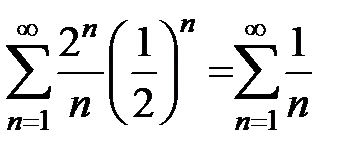. Получили гармонический ряд, который, как известно, расходится.

Итак, область сходимости – 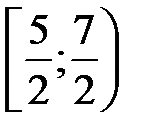(к интервалу сходимости присоединился один из его концов).4

9.193. Сформулировать теорему Абеля для ряда (6).

9.194. Степенной ряд по степеням 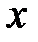сходится в точке 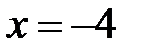. Является ли этот ряд в точке 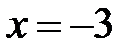абсолютно сходящимся, условно сходящимся или расходящимся?

9.195. Пусть 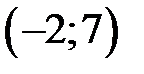– интервал сходимости степенного ряда по степеням 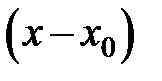. Найти .

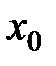9.196. Пусть 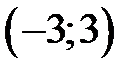– интервал сходимости степенного ряда 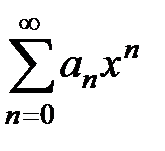. Какой интервал сходимости имеет степенной ряд ?

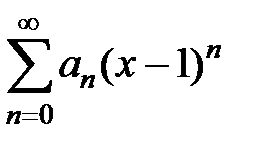9.197. Пусть 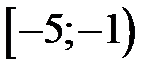– область сходимости степенного ряда 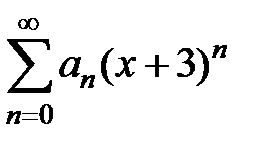. Является ли ряд 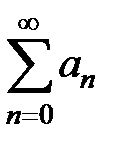абсолютно сходящимся, условно сходящимся или расходящимся?

9.198. Радиусы сходимости двух степенных рядов по степеням 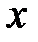равны 5 и 6 (соответственно). Какой радиус сходимости имеет сумма этих рядов?

Найти радиус, интервал и область сходимости степенных рядов .

9.199. 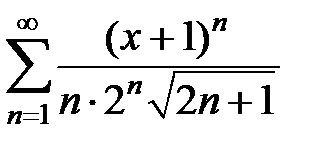.	9.200. .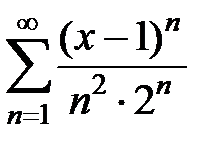
9.201. 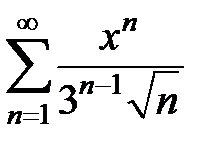.	9.202. .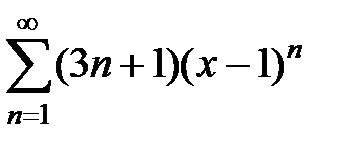
9.203. 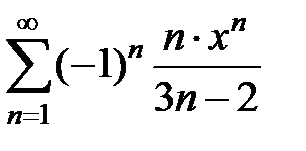.	9.204. .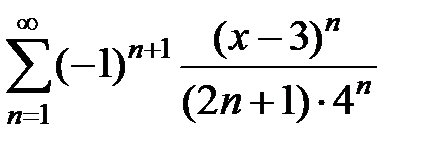
9.205.