Экспериментальные методы исследования закона дисперсии фононов
Наиболее мощный метод исследования закона дисперсии фононов — комбинационное рассеяние разного типа частиц (волн) на колебаниях кристаллической решетки. Это неупругое рассеяние: частица (волна), взаимодействуя с колебаниями решетки, меняет не только направление движения, но и энергию (частоту).
Рассмотрим комбинационное рассеяние света. Пусть на кристалл падает пучок монохроматического света с волновым вектором 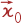 и частотой
и частотой 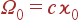 (рис. 7).
(рис. 7).
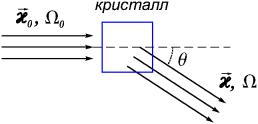 Рис. 7. Рис. 7. |
Если исследовать спектр света, рассеянного кристаллом в определенном направлении, то в простейшем случае он будет иметь вид, изображенный на рис. 8.
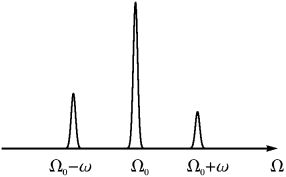 Рис. 8. Рис. 8. |
Помимо высокого центрального пика, расположенного на частоте падающего света Ω0 (упругое рассеяние), появляются еще два сателлита, сдвинутых влево и вправо на частоту длинноволнового оптического фонона ω:
| Ω = Ω0±ω | (67) |
Левый пик называют стоксовым, правый — антистоксовым.
Изменение частоты при рассеянии невелико, т. к. частота оптического фонона меньше частоты света в десятки раз. Действительно, характерная энергия кванта света, ħΩ0, равна 1 эВ, а энергия оптического фонона по нашей оценке (см.) составляет около 50 мэВ.
Если в кристалле имеется несколько ветвей оптических фононов, то в спектре комбинационного рассеяния будет наблюдаться несколько пар сателлитов.
Частоты, на которых располагаются линии спектра рассеянного света являются ''комбинациями'' частоты падающего света Ω0 и частоты фонона ω. Из-за этого рассеяние и называется комбинационным.
Впервые эффект комбинационного рассеяния был экспериментально обнаружен и объяснен Г. С. Ландсбергом и Л. И. Мандельштамом в 1928 г.; в экспериментах использовались кристаллы кварца и исландского шпата. В том же году Ч. В. Раман обнаружил комбинационное рассеяние в жидкостях, поэтому эффект комбинационного рассеяния также называют эффектом Рамана, а рассеяние — рамановским. В 1930 г. Раману за обнаружение комбинационного рассеяния была присуждена Нобелевская премия.
Комбинационное рассеяние наблюдается не только в твердых телах. Например, при рассеянии на молекулах газа сдвиг линий комбинационного рассеяния будет определятся частотой колебаний атомов в молекуле. Если у молекулы несколько колебательных степеней свободы, то в спектре рассеянного излучения будет наблюдаться несколько линий.
Возникает вопрос: почему при комбинационном рассеянии на кристалле получаются столь узкие пики (линии) излучения? Ведь оптические фононы имеют дисперсию и их частоты занимают достаточно широкий непрерывный интервал? Дело в том, что свет, рассеиваемый в данном направлении, взаимодействует только со строго определенным колебанием решетки. Проще всего показать это, описывая рассеяние на квантовом языке, хотя тот же результат можно получить и в рамках классической физики.
В квантовой механике каждой волне соответствует квазичастица (а частице — волна). Электромагнитному полю соответствуют фотоны, колебаниям решетки — фононы.
Явление комбинационного рассеяния заключается в том, что фотон падающего на кристалл света либо испускает фонон (стоксов процесс), либо поглощает его (антистоксов процесс). Эти процессы можно проиллюстрировать соответствующими фейнмановскими диаграммами (рис. 9).
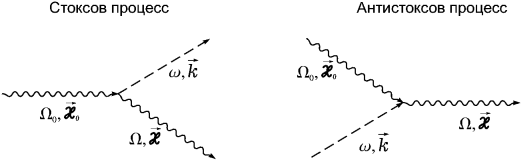 Рис. 9. Рис. 9. |
Энергия и импульс должны сохраняться, т. е. при рассеянии импульс и энергия фотона уменьшается (стоксов процесс) или увеличивается (антистоксов процесс) на импульс и энергию фонона соответственно.
Фотон падающего на кристалл света имеет энергию ħΩ0 и импульс 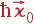 , рассеянный фотон — энергию ħΩ и импульс
, рассеянный фотон — энергию ħΩ и импульс 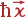 . Энергия и импульс фонона равны ħω и
. Энергия и импульс фонона равны ħω и 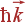 , где ω – частота, а
, где ω – частота, а 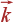 — волновой вектор фонона.
— волновой вектор фонона.
Таким образом:
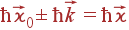 | (68) |
 | (69) |
Здесь знак ''–'' соответствует стоксовому процессу, ''+'' — антисотксовому.
На постоянную Планка можно сократить:
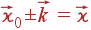 | (70) |
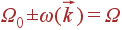 | (71) |
То, что постоянная Планка не входит в эти уравнения, свидетельствует о том, что к такому же результату можно было прийти, описывая рассеяние языком классической физики.
Частота света и колебаний решетки являются функциями соответствующих волновых векторов:  ,
, 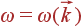 . Поэтому, если задать направление и частоту падающего света и направление рассеяния, а также ветвь колебаний решетки, то уравнения (70) и (71) будут однозначно определять волновой вектор колебания решетки
. Поэтому, если задать направление и частоту падающего света и направление рассеяния, а также ветвь колебаний решетки, то уравнения (70) и (71) будут однозначно определять волновой вектор колебания решетки 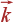 и изменение частоты рассеянного света.
и изменение частоты рассеянного света.
Как уже говорилось, характерные энергии оптических фононов (~ 50 мэВ) много меньше характерных энергий фотонов видимого света (~ 1 эВ). Другими словами, частота и, соответственно, длина волнового вектора фотона при рассеянии меняются мало: 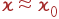 . Поэтому, как видно из рис. 10, длина волнового вектора фонона, участвующего в рассеянии, приблизительно равна
. Поэтому, как видно из рис. 10, длина волнового вектора фонона, участвующего в рассеянии, приблизительно равна  , где θ — угол рассеяния. Максимального значения
, где θ — угол рассеяния. Максимального значения 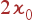 она достигает при θ = π, т. е. при рассеянии света назад.
она достигает при θ = π, т. е. при рассеянии света назад.
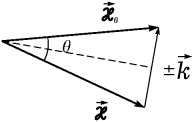 Рис. 10. Рис. 10. |
Длина волны света видимого диапазона по порядку величины равна 1 мкм = 104Å. Поэтому в комбинационном рассеянии света участвуют только длинноволновые фононы, волновой вектор которых (k~ 10–4Å) очень мал по сравнению с размерами зоны Бриллюэна (π/a~ 1 Å–1).
Частота оптических фононов с такими волновыми векторами практически не отличается от  , см. рис. 11. Поэтому смещение стоксовой и антистоксовой линий при комбинационном рассеянии на оптических фононах не зависит от направления рассеяния и равно ω0. Таким образом, по спектру комбинационного рассеяния можно определить лишь одну точку дисперсионной зависимости оптических фононов.
, см. рис. 11. Поэтому смещение стоксовой и антистоксовой линий при комбинационном рассеянии на оптических фононах не зависит от направления рассеяния и равно ω0. Таким образом, по спектру комбинационного рассеяния можно определить лишь одну точку дисперсионной зависимости оптических фононов.
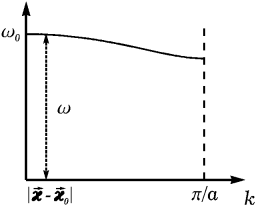 Рис. 11. Рис. 11. |
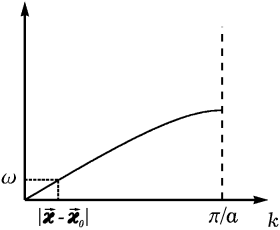 Рис. 12. Рис. 12. |
Мандельштам и Ландсберг в своих первых экспериментах по комбинационному рассеянию предполагали обнаружить рассеяние на акустических, а не на оптических колебаниях решетки. Изменение частоты при таком рассеянии намного меньше, чем при рассеянии на оптических фононах (рис. 12) и может быть обнаружено лишь при очень хорошем спектральном разрешении измерительных приборов.
Рассеяние на акустических фононах действительно наблюдается и носит название рассеяния Мандельштама-Бриллюэна.
Закон дисперсии акустических колебаний при малых волновых векторах линеен: ωак = sk, где s — скорость звука. Поэтому изменение частоты света при рассеянии на угол θ равно:
 | (72) |
Видно, что относительное изменение частоты очень мало. Скорость света в кристалле по порядку величина равна 108м/с, скорость звука — 103м/с, поэтому s/c~ 10–5. Отметим также, что при рассеянии на акустических фононах изменение частоты света зависит от угла рассеяния, см. рис. 12. (При рассеянии на оптических колебаниях сдвиг частоты равен ω0 независимо от направления рассеяния).
На спектре комбинационного рассеяния (рис. 8) высота стоксового пика больше чем антистоксового. Этому явлению легко дать качественное объяснение: для того, чтобы поглотить фонон, нужно, чтобы он в кристалле был, а испустить фонон можно, казалось бы, и ''на пустом месте'', без помощи других фононов. Поэтому при низких температурах, когда фононов мало, интенсивность антистоксовой линии намного меньше, чем стоксовой.
Однако, не все так просто: как показал Эйнштейн, имеющиеся в кристалле фононы ''помогают'' излучению фононов (вынужденное излучение). Вынужденное излучение будет более подробно рассмотрено ниже в применении к свету, а пока лишь скажем, что вероятность рассеяния с поглощением фонона пропорциональна числу фононов данного типа N, а вероятность обратного процесса — рассеяния с испусканием фонона — пропорциональна N+1. Единица в последнем выражении как раз и соответствует испусканию фонона ''на пустом месте'' (спонтанному излучению).
Если пренебречь малым изменением частоты при рассеянии, то коэффициенты пропорциональности в этих вероятностях можно считать одинаковыми. В состоянии термодинамического равновесия число фононов данного типа с частотой ω описывается распределением Бозе-Эйнштейна:
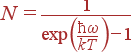 | (73) |
Отсюда для отношения интенсивностей стоксовой и антистоксовой линий получаем:
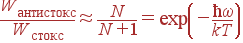 | (74) |
Это отношение позволяет по данным рассеяния измерить температуру кристалла. Интенсивности стоксовой и антистоксовой линий сильно различаются при низких температурах, когда kT<ħω. При kT>>ħω, в классическом пределе, интенсивности обеих линий равны.
Итак, мы рассмотрели комбинационное рассеяние света на оптических и акустических колебаниях решетки. Один из выводов этого рассмотрения состоит в том, что в рассеянии участвуют лишь длинноволновые фононы. Поэтому с помощью комбинационного рассеяния света видимого диапазона можно получить информацию только о длинноволновой части фононного спектра: определить частоты 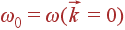 для оптических фононов и скорость звука s для акустических.
для оптических фононов и скорость звука s для акустических.
Как с помощью комбинационного рассеяния исследовать весь фононный спектр, в частности, область больших волновых векторов? Для этого нужно изучать рассеяние частиц (или квазичастиц), длина волны которых сравнима с постоянной решетки: в рассеянии таких частиц могут участвовать коротковолновые фононы.
Электромагнитное излучение с такими длинами волн принадлежит рентгеновскому диапазону, мы уже рассматривали упругое рассеяние рентгеновских волн на неподвижной идеальной кристаллической решетке. Энергия кванта такого излучения по порядку величины равна 10000 эВ. Напомним, что энергия оптического фонона составляет 0.03-0.1 эВ: заметить такое изменение на фоне 10000 эВ очень трудно.
Поэтому для изучения коротковолнового фононного спектра в качестве рассеивающихся частиц используют нейтроны. Нейтрон нейтрален, он слабо взаимодействует с электронной системой кристалла. Но главное, энергия нейтрона, обладающего длиной волны порядка постоянной решетки, сравнима с энергией фонона:
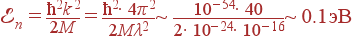 | (75) |
Энергии нейтронов, испускаемых при ядерных реакциях, на много порядков больше, поэтому, чтобы использовать нейтроны для исследования фононного спектра, приходится их замедлять.
Зная энергию падающего нейтрона и нейтрона, рассеянного в определенном направлении, мы можем определить энергию и импульс фонона, воспользовавшись законами сохранения энергии и импульса:
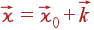 | (76) |
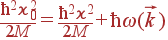 | (77) |
Меняя энергию нейтронов и направление рассеяния, можно исследовать закон дисперсии фононов.
На самом деле, в спектре рассеянных нейтронов будут также присутствовать пики, вызванные рассеянием с участием нескольких фононов.
Необходимо сделать одно замечание о законе сохранения импульса (76).
Из-за дискретности кристаллической решетки волновые вектора 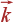 и
и 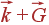 соответствуют одному и тому же фонону. (Здесь
соответствуют одному и тому же фонону. (Здесь  — произвольный вектор обратной решетки). Поэтому мы условились описывать колебания волновыми векторами, лежащими в первой зоне Бриллюэна, т.к. любой вектор можно перенести в первую зону, прибавляя к нему вектора обратной решетки.
— произвольный вектор обратной решетки). Поэтому мы условились описывать колебания волновыми векторами, лежащими в первой зоне Бриллюэна, т.к. любой вектор можно перенести в первую зону, прибавляя к нему вектора обратной решетки.
В комбинационном рассеянии света участвуют фононы с малыми волновыми векторами, которые автоматически оказываются в первой зоне Бриллюэна.
Волновой вектор нейтрона сравним с размерами первой зоны Бриллюэна. В связи с этим может возникнуть вопрос: распространяется ли ограничение волновых векторов фононов первой зоной Бриллюэна на закон сохранения импульса (76)?
Оказывается, что нет: формально в рассеянии может участвовать фонон с произвольным волновым вектором. Мы можем рассматривать частоту фононов, как периодическую функцию 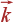 , не ограничиваясь первой зоной Бриллюэна. При этом надо помнить, что волновые вектора, отличающиеся на вектор постоянной решетки, описывают одно и тоже колебание.
, не ограничиваясь первой зоной Бриллюэна. При этом надо помнить, что волновые вектора, отличающиеся на вектор постоянной решетки, описывают одно и тоже колебание.
Есть другая возможность: считать что 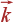 обязательно лежит в первой зоне Бриллюэна, но вместо (76) писать закон сохранения импульса в следующей форме:
обязательно лежит в первой зоне Бриллюэна, но вместо (76) писать закон сохранения импульса в следующей форме:
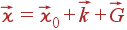 | (78) |
Здесь  — произвольный вектор обратной решетки. Можно считать, что мы пишем закон сохранения импульса для трех частиц: нейтрона, фонона и кристалла как целого. При этом кристалл как целое может отдать или забрать не любой импульс, а лишь импульс, соответствующий произвольному вектору обратной решетки
— произвольный вектор обратной решетки. Можно считать, что мы пишем закон сохранения импульса для трех частиц: нейтрона, фонона и кристалла как целого. При этом кристалл как целое может отдать или забрать не любой импульс, а лишь импульс, соответствующий произвольному вектору обратной решетки  .
.
