Лекция 1. Виды нелинейности. Нелинейная упругость

В линейной механике используется, во-первых, принцип суперпозиции, т.е. считается, что от перемены порядка воздействия результат не меняется, причем, результат от одновременных воздействий можно получить путем сложения результатов от поочередных воздействий. Во-вторых, считается, что во сколько раз увеличивается воздействие, во столько раз увеличивается и отклик (закон Гука, второй закон Ньютона, закон Винклера и т.д.).

В нелинейной механике нарушается или то, или другое, а чаще и то, и другое.

Причины нелинейности в МДТТ:

1. Физическая нелинейность, т.е. нелинейная зависимость напряжений и деформаций. σ=σ(ε)

Примеры:

σ σ

сталь бетон

ε ε

2. Неупругие свойства (ползучесть, пластичность, растрескивание).

3. Сильное изменение геометрии конструкции, которое приводит к изменению направления действия внешних сил.

4. Конструктивная нелинейность. Возникает, когда при некоторых нагрузках в работу включаются не работавшие до этого элементы или связи. Например, при некотором перепаде температур подключается в работу правая

опора и появляются напряжения.

5. Нелинейные задачи возникают при оптимизации конструкции, поскольку неизвестными являются напряжения, деформации и геометрические характеристики, которые входят в уравнения равновесия в виде произведений функций, зависящих от них.

Получение нелинейных диаграмм деформирования.

σ3 σ4

σ2

σ1

Для решения задач с физической нелинейностью необходимо найти функцию σ=σ(ε). Аппроксимация σ должна отвечать физическому смыслу.

При использовании полинома степень не должна быть больше 3.

Е₀ – стандартный ГОСТ-й модуль упругости.

Е₁, Е₂ – необходимо найти.

Дано: σ=6 МПа; σ=11 МПа; σ=18 МПа; σ=16МПа; ε=0,001; ε=0,0015; ε=0,002; ε=0,003; Е₀=30000 МПа.

Найти: Е₁, Е₂

Решение: Т.к. число уравнений больше числа неизвестных, то используем условие минимума невязки между экспериментальными и расчетными значениями σ.

Перепишем уравнение

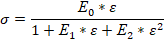
в виде: Е₁*ε+Е₂*ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> =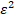

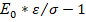
Подставив значения, получим:

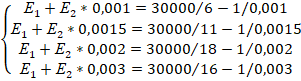
Используем метод минимизации квадратичной невязки.

Пусть имеется переопределенная система уравнений .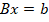

Найдем невязку .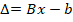

В качестве нормы . .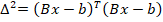

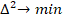По теореме Ферма .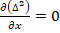

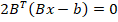
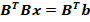
Запишем матрицы:

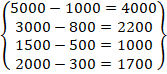B= b= x=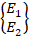

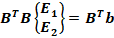
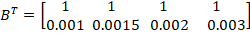
Получим:

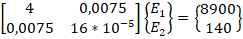
Решение Е₁=8,1*10²

Е₂=4,2*10⁴

Примечание:

1. Е₀, Е₁, Е₂ называются механическими характеристиками материала.

Е₀ – начальный модуль упругости. Е₀=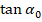

Е= 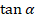- секущий модуль упругости.

Δσ

Δε

α₀ α

По ГОСТ 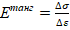– тангенциальный модуль упругости.

Тангенциальный модуль упругости используется редко, поскольку требует сложных методов расчета (метод Ньютона).

2. К сожалению, задачи отыскания механических характеристик Е₁, Е₂, Е₀

является, как правило, математически неустойчивой, т.е. малые изменения экспериментальных данных вызывают большие изменения Е₁, Е₂.