Проверочный расчет зубчатой передачи

Проверим межосевое расстояние:

а_w = (d₁ + d₂) /2 = (56,79 + 223,12) /2 = 140 мм.

Проверим контактные напряжения s_н, МПа:

,

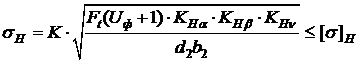где K – вспомогательный коэффициент. Для косозубых передач K = 376, а для прямозубых K = 436;

Ft = 2Т₂ × 10³ / d₂ – окружная сила в зацеплении, Н, для нашего случая, где Т₂ = Т₃ имеем,

Ft = 2Т₃ × 10³ / d₂= 2 × 448 × 10³ / 223,12 = 4015,7 Н.

Кнa – коэффициент, учитывающий распределение нагрузки между зубьями: определяем по графику (рис. 4) в зависимости от окружной скорости колес ν = w₃ d₂ / (2 × 10³), м/с и степени точности передачи получаем 9 по (табл. 4):

ν= 11,5×223,12 / (2 × 10³)= 1,28 м/с.

Принимаем по графику, Кнa= 1,11.

Кнn – коэффициент динамической нагрузки определяем по табл. 5, в зависимости от окружной скорости колес и степени точности передачи (табл. 4),

Кнn= 1,01.

Кн_β, U_ф, d₂, b₂ – значения перечисленных величин определяли ранее.

Подставим полученные величины, имеем, что

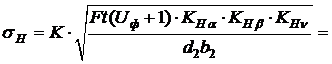
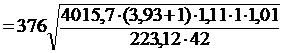= 578,6 МПа.

Полученное значение контактного напряжения sн меньше допускаемого [s]н = 640 МПа.

Определим степень недогрузки по контактным напряжениям:

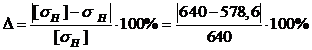= 9,5%.

Допускаемая недогрузка передачи (s_н < [s]_н) не более 10% и перегрузка (s_н > [s]_н) до 5%. Если условие прочности не выполняется, то следует изменить ширину венца колеса b₂. Если эта мера не даст должного результата, то либо надо увеличить межосевое расстояние а_w, либо назначить другие материалы колес или другую термообработку, пересчитать допускаемые контактные напряжения и повторить весь расчет передач.

Проверим напряжение изгиба зубьев шестерни s_F1 и колеса s_F2, МПа:

,

,

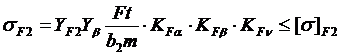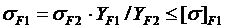где m – модуль зацепления, m = 2 мм; b₂ = 42 мм, ширина венца зубчатого колеса; F_t = 4015,7 Н, окружная сила в зацеплении; КFa – коэффициент, учитывающий распределение нагрузки между зубьями, зависит для косозубых от степени точности передачи.

Степень точности 6 7 8 9

Коэффициент КFa 0,72 0,81 0,91 1,00

Для прямозубых КFa = 1, задается.

К_Fβ – коэффициент неравномерности нагрузки по длине зуба, выбираем аналогично К_Нβ, К_Fβ = 1; КFν – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи (см. табл. 5), К_Fν = 1,05; Y_F1 и Y_F2 – коэффициенты формы зуба шестерни и колеса. Определяются по табл. 6 в зависимости от числа зубьев шестерни Z₁ и колеса Z₂ для прямозубых, а для косозубых – в зависимости от эквивалентного числа зубьев шестерни и колеса,

Zn₁ = Z₁ / cos³b и колеса Zn₂ = Z₂ / cos³b,

где β – угол наклона зубьев, определяемый ранее.

Zn₁ = Z₁ / cos³b = 28 / cos³9,6° = 29.

Zn₂ = Z₂ / cos³b = 110 / cos³9,6° = 115.

По табл.6 имеем: Y_F1 = 3,8; Y_F2 = 3,6.

Y_β = 1 – b° /140° – коэффициент, учитывающий наклон зуба,

Y_β = 1 – 9,6°/140° = 0,93.

[s]_F1 = 314 МПа и [s]_F2 = 294 МПа – допускаемые напряжения изгиба шестерни и колеса (определены ранее).

Подставим известные величины и определим:

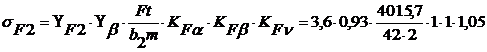= 168 МПа

s_F1 = s_F2 × Y_F1 / Y_F2 = 168 · 3,8 / 3,60 = 177,4 МПа.

Проверочный расчет показал, что расчетные значения s_F значительно меньше [s]_F, это допустимо, т.к. нагрузочная способность большинства зубчатых передач и рассматриваемого примера в частности, ограничивается контактной прочностью. Если s_F > [s]_F свыше 5%, то надо увеличить модуль m, соответственно пересчитать число зубьев шестерни Z₁ и колеса Z₂ и повторить проверочный расчет на изгиб. При этом межосевое расстояние а_w не изменяется, а следовательно, не нарушается контактная прочность передачи.