Равномерное распределение ДСВ
Виды распределений случайных величин
Равномерное распределение ДСВ
Случайная величина 
, принимающая целые значения от 1 до 
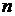, имеет равномерное распределение, если
.
Найдем математическое ожидание и дисперсию равномерно распределенной случайной величины :
;
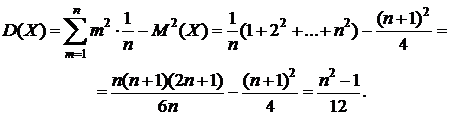
Пример. Имеется связка из 5 ключей, из которых только один подходит к открываемому замку. Найти распределение случайной величины – числа ключей, которые пришлось опробовать прежде, чем открыли замок.
Очевидно, может принимать значения от 1 до 5, вероятности которых можно вычислить так:
; 
.
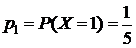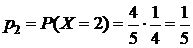Если 
, значит, опробованы 2 ключа. Данное событие представляет собой произведение двух событий: первый ключ не подошел, вероятность 4/5, второй подошел – вероятность 1/4.
Далее рассуждаем аналогично:
; 
;
.
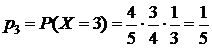Биномиальное распределение ДСВ
Случайная величина , принимающая целые значения от 0 до 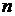, имеет биномиальное распределение, если
.
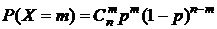Такое распределение имеет случайная величина , равная числу осуществлений некоторого события А в серии из 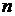испытаний, в каждом из которых вероятность появления события А постоянна и равна 
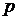. Числовые характеристики биномиального распределения можно найти по формулам:
.
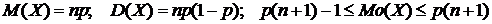Пример. В корзине 50 шаров, из них 10 черных. Достают 5 шаров, причем выборка осуществляется с возвращением. Охарактеризовать случайную величину Х — число обнаруженных в выборке шаров черного цвета.
Величина Х может принимать значения от 0 до 5, т. к. выборка проводится с возвращением, вероятность 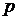обнаружить всякий раз черный шар постоянна и равна 10/50 = 0,2. Вероятности каждого значения вычислим по формуле Бернулли:
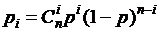, где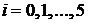 
.
Получим ряд распределения:
 | ||||||
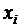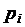 | 0,32768 | 0,4096 | 0,2048 | 0,0512 | 0,0064 | 0,00032 |
Найдем функцию распределения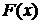 
:
 |  |  |  |  |  |  |  |
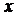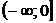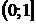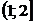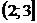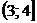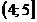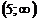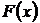 | 0,32768 | 0,73728 | 0,94208 | 0,99328 | 0,99968 |
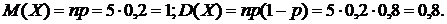
Наивероятнейшее значение ( 
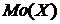) определяется из неравенства
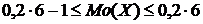или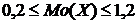 
.
Целым значением, удовлетворяющим этим двум неравенствам, является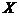 
= 1. Значит, 
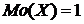, что видно и из ряда распределения.
Распределение Пуассона ДСВ
Случайная величина , принимающая бесконечное множество значений 0,1,2… имеет распределение Пуассона, если
,
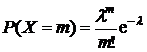где 
– параметр распределения, имеет смысл среднего числа наступлений события за единицу времени. Величины, которые подчиняются подобному распределению, были описаны в разделе.
Числовые характеристики пуассоновского распределения:
.
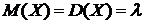Виды распределений случайных величин
Равномерное распределение ДСВ
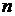Случайная величина , принимающая целые значения от 1 до , имеет равномерное распределение, если
.
Найдем математическое ожидание и дисперсию равномерно распределенной случайной величины :
;
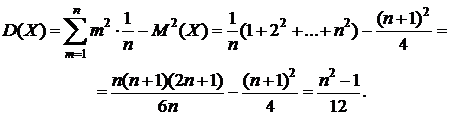
Пример. Имеется связка из 5 ключей, из которых только один подходит к открываемому замку. Найти распределение случайной величины – числа ключей, которые пришлось опробовать прежде, чем открыли замок.
Очевидно, может принимать значения от 1 до 5, вероятности которых можно вычислить так:
; .
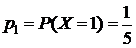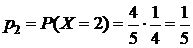Если , значит, опробованы 2 ключа. Данное событие представляет собой произведение двух событий: первый ключ не подошел, вероятность 4/5, второй подошел – вероятность 1/4.
Далее рассуждаем аналогично:
; ;
.
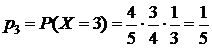