Разложение функции в степенной ряд. Ряд Тейлора
Определение 3.1.Если для функции f(x) справедливо равенство:
f(x) = c0+c1(x-a)+c2(x-a)2+¼+cn(x-a)n+¼, 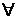 xÎХ, (3.1)
xÎХ, (3.1)
то говорят, что функция f(x) разложена в степенной ряд на множестве Х, а сам ряд называют её разложением по степеням разности 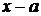 .
.
Заметим, что согласно (3.1) функция f(x) является суммой степенного ряда на множестве Х.
Теорема 3.1(о единственности разложения функции в степенной ряд). Пусть функция f(x) разложена в степенной ряд на некотором промежутке Х в соответствии с равенством (3.1), то
1) функция f(x) имеет на промежутке Х производные любого порядка;
2) это разложение единственно.
► По условию, равенство (3.1) имеет место при любом x из промежутка Х. Положив в этом равенстве x = a, получим c0 = f(a).
Равенство (3.1) можно почленно дифференцировать сколько угодно раз. Имеем:
f¢(x) = c1 + 2c2(x-a) + 3c3(x-a)2 + ¼ + ncn(x-a)n-1 + ¼,
f²(x) = 2×1×c2 + 3×2×c3(x-a) + ¼ + n(n - 1)cn(x-a)n-2 + ¼,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
f (k)(x) = k!ck + (k+1) k …2ck+1(x-a) + ¼ + n(n - 1)…(n−k+1)cn(x-a)n-k + ¼,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . .
Положим в этих равенствах x = a, получим:
c1 = f¢(a), f²(a) = 2!c2× Þ 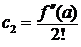 ; … f (k)(a) = k!ck× Þ
; … f (k)(a) = k!ck× Þ 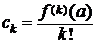 ,… .
,… .
Заменим в последнем равенстве k на n:
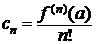 , n = 1, 2, ¼ . (3.2)
, n = 1, 2, ¼ . (3.2)
Итак, для коэффициентов ряда из правой части (5.1) всегда справедливо равенство (5.2) независимо от того, как было получено это разложение.◄
Подставим (5.2) в (5.1):
f(x) = f(a)+f¢(a)(x-a)+ 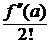 (x-a)2+¼+
(x-a)2+¼+ 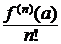 (x-a)n+¼=
(x-a)n+¼=
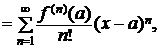
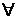 xÎХ, (3.3)
xÎХ, (3.3)
Ряд из равенства (3.3) называется рядом Тейлора функции f(x). Из теоремы 3.1 следует, что если функция f(x) разложена в степенной вида (3.1), то это всегда её ряд Тейлора.
Теорема, обратная теореме 3.1 не верна, т. е. функция, имеющая производные любого порядка на множестве Х, может быть не представима на нём своим рядом Тейлора.
Теорема 3.2(необходимое и достаточное условие разложения функции в ряд Тейлора). Пусть функция f(x) имеет производные любого порядка на множестве Х. Для того, чтобы f(x) могла быть разложена в ряд Тейлора на множестве Х, необходимо и достаточно, чтобы остаточный член Rn(x) её формулы Тейлора стремился к нулю при 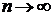 для
для 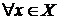 .
.
►Напишем для функции f(x) формулу Тейлора:
f(x) = f(a)+f¢(a)(x-a)+ 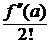 (x-a)2+¼+
(x-a)2+¼+ 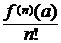 (x-a)n+Rn(x) или
(x-a)n+Rn(x) или
f(x) = Tn(x)+Rn(x), (3.4)
где Tn(x)= f(a)+f¢(a)(x-a)+ 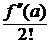 (x-a)2+¼+
(x-a)2+¼+ 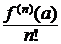 (x-a)n − многочлен Тейлора. Очевидно, что Tn(x) есть частичная сумма ряда Тейлора, т.е. Tn(x)=Sn(x). Тогда (3.4) преобразуется к виду:
(x-a)n − многочлен Тейлора. Очевидно, что Tn(x) есть частичная сумма ряда Тейлора, т.е. Tn(x)=Sn(x). Тогда (3.4) преобразуется к виду:
f(x) = Sn(x)+Rn(x), (3.5)
Из равенства (3.5) следует:
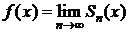 ,
, 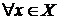
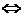 Rn(x)
Rn(x) 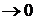 при
при 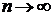 для
для 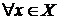 .◄
.◄
Разложение некоторых элементарных функций
В ряды Маклорена
Пусть функция f(x) имеет производные любого порядка в некоторой окрестности точки 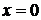 . В равенстве (3.3) положим a = 0, ряд (3.3) принимает вид:
. В равенстве (3.3) положим a = 0, ряд (3.3) принимает вид:
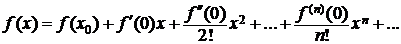
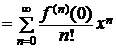 . (4.1)
. (4.1)
Ряд (4.1) называют рядом Маклорена. Ряд Маклорена − это ряд по степеням х.
Напишем для f(x) формулу Маклорена с остаточным членом в форме Лагранжа:
 ,
, 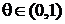 . (4.2)
. (4.2)
Используя равенство (4.2) и теорему 3.2, разложим в ряд Маклорена функции: ex , sin x, cos x, ln(1 + x), acrtg x, (1+ x)α. Предварительно докажем лемму.
Лемма. 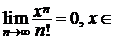 R.
R.
►Рассмотрим ряд 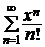 и исследуем его на абсолютную сходимость по признаку Даламбера. Имеем:
и исследуем его на абсолютную сходимость по признаку Даламбера. Имеем:
 при
при  R.
R.
Данный ряд сходится абсолютно на всей вещественной оси, поэтому его общий член стремится к нулю при 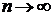 при
при  R, т.е.
R, т.е. 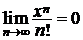 .◄
.◄
1. 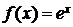 ,
,  R. Имеем f (n)(x) = ex, f (n)(0) = 1, f(n+1)(θх) = eθх для
R. Имеем f (n)(x) = ex, f (n)(0) = 1, f(n+1)(θх) = eθх для  R и
R и 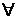 nÎN. Напишем для f(x) = exформулу Маклорена вида (4.2):
nÎN. Напишем для f(x) = exформулу Маклорена вида (4.2):
 ,
, 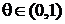 .
.
Для остаточного члена Rn(x)  справедливо неравенство:
справедливо неравенство:
 для
для  R.
R.
Отсюда следует с учётом леммы, что Rn(x) 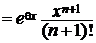
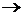 0 при
0 при 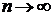 для
для  R. Но тогда ряд Маклорена
R. Но тогда ряд Маклорена
 (4.3)
(4.3)
в силу теоремы 4.2 сходится к функции exвсей вещественной оси.
2. f(x) = sinx,  R. Имеем f (n)(x) =
R. Имеем f (n)(x) =  ,
,
f (n)(0) = 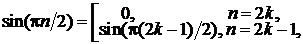
f (n+1)(θх) =  для
для  R и
R и 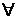 n Î N,
n Î N, 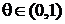
Имеем 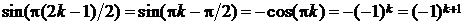 ,
, 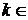 Z. Отсюда для производных от функции f(x) = sinx в точке х = 0 имеем равенство:
Z. Отсюда для производных от функции f(x) = sinx в точке х = 0 имеем равенство:
f (2k)(0)=0, f (2k−1)(0)=(−1)k+1.
Напишем для f(x) = sinx формулу Маклорена вида (6.2):
 ,
, 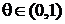 .
.
Для остаточного члена Rn(x)  верно неравенство:
верно неравенство:
 для
для  R.
R.
Отсюда, с учётом леммы, следует, что Rn(x) 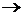 0 при
0 при 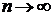 для
для  R. Но тогда ряд Маклорена
R. Но тогда ряд Маклорена
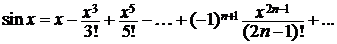 (4.4)
(4.4)
в силу теоремы 4.2 сходится к функции sinx на всей вещественной оси.
3.f(x) = cosx,  R. Ряд Маклорена можно получить, рассуждая так же, как в случае функции sinx. Однако рациональнее применить теорему о почленном дифференцировании степенного ряда. Запишем ряд (6.4) в несколько ином виде:
R. Ряд Маклорена можно получить, рассуждая так же, как в случае функции sinx. Однако рациональнее применить теорему о почленном дифференцировании степенного ряда. Запишем ряд (6.4) в несколько ином виде:
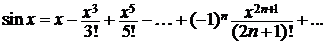
и продифференцируем обе части полученного равенства:
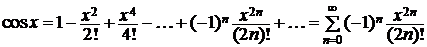 ,
, 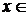 R. (4.5)
R. (4.5)
