Нелинейные резистивные цепи постоянного тока

6.1.1. Для стабилизации тока в нагрузке R_н используются параллельно включенные позистор (рис.74.а), ВАХ которого приведена на рис.74.б и резистор с сопротивлением R.

а) б)

Рис.74. Схема цепи и ВАХ позистора

Подобрать значение R так, чтобы ток 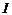был постоянен при изменении напряжения на позисторе от 3 до 10 В. Найти ток стабилизации .

Решение:

Чтобы цепь работала как стабилизатор тока, нужно подобрать такое сопротивление R, при котором суммарная ВАХ параллельной цепи имеет горизонтальный участок (I=const). Это достигается при равенстве сопротивления R резистора модулю дифференциального сопротивления позитрона на падающем участке ВАХ. Следовательно, на участке 3≤U≤10 В (см. рис. 74.б), дифференциальное сопротивление позитрона:

Тогда Ток стабилизации можно определить аналитически для любого значения напряжения на данном участке, например для U=10 В:

Ток стабилизации можно получить графически, сложив ординаты ВАХ позитрона и резистора (см. рис.74,б).

6.1.2. Рассчитать ток в нелинейном резисторе при питании цепи (рис.75.а) от источника ЭДС Е=24 В. ВАХ нелинейного резистора представлена на рис.75.б. Параметры цепи: R₁=R₂=4 Ом, R₃=3 Ом; R₄=1 Ом. Найти токи в остальных ветвях цепи.

а)

б)

Рис.75. Схема цепи и ВАХ нелинейного резистора

Решение:

Задачу целесообразно решить методом эквивалентного генератора. Размыкаем ветвь bd и находим напряжение на разомкнутых зажимах Ubdxx . Определим входное сопротивление без ветви с Rнр.

Э.Д.С. эквивалентного источника равна . Далее, закоротим E и определим входное сопротивление относительно разомкнутых зажимов bd.

Итак, параметры эквивалентного генератора: Eэкв=6 В. Rвн=1.5 А (см. рис. 75,в)

Рис.75в.

На ВАХ нелинейного резистора построим нагрузочную характеристику:

Точка пересечения ВАХ нелинейного резистора с нагрузочной характеристикой (т. А) даёт рабочий режим цепи:

Используя эти данные, определим остальные токи в цепи:

Проверка:

6.1.3. Рассчитать ток в нелинейном резисторе при питании цепи (рис.75.а) от источника тока J=2А, ВАХ нелинейного элемента дана на рис. 75.б. Параметры цепи R₁=R₂=4Ом; R₃=3Ом, R₄=1Ом. Определив режим работы нелинейного резистора, определить токи в остальных ветвях цепи.

Ответы:

А;

Примечание: При расчёте внутреннего сопротивления эквивалентного генератора ветвь с источником тока I разомкнуть. Тогда:

6.1.4. В схеме на рис.76.а рассчитать токи во всех ветвях, ВАХ нелинейно го элемента дана на рис.76.б Параметры цепи: Е=20В, J=3A, R₁=R₂=R₃=2Ом

а) б)

в) Рис.76. Схема цепи и ВАХ нелинейного резистора

Решение:

Задачу решаем методом эквивалентного генератора. Находим параметры эквивалентного генератора, размыкаем ветвь с нелинейным элементом и находим Uabxx. По второму закону Кирхгофа:

Для определения внутреннего сопротивления эквивалентного генератора размыкаем ветвь с источником тока, а ЭДС закорачваем.

Получаем следующую цепь (см. рис. 76,г).

Нагрузочная характеристика нелинейного элемента:

Строим эту характеристику на ВАХ НР. Рис.76.г

Точка пересечения А дает рабочий режим цепи. Из графика вычисляем:

Рис. 77,г

6.1.5. Заменить нелинейный активный двухполюсник (рис.77.а) эквивалентным и определить его параметры, если Е₁=Е₂=30В. ВАХ нелинейного резистора заданы на рис.77.б

Рис.77. Активный двухполюсник и ВАХ нелинейных резисторов

Решение:

Смотрим решение задачи 6.1.14.

Ответы:

EЭ= 20 В, направлена в точке в.

U,В	I,А	U,В	I,А
-20	-6.5		0.5
-10	-3.25

6.1.6. Показать, что напряжение на выходе схемы рис.78.а пропорционально произведению напряжений U₁ и U₂, если ВАХ цепочки, состоящей из последовательно соединенных диода Д и резистора R, описывается квадратичной зависимостью I=BU²

Примечание: на рис.78б) напряжение U₂ направлено противоположно току I₃.

а) б)

Рис.78. Схемы цепей

а

Решение:

По второму закону Кирхгофа имеем:

;

6.1.7.К цепи, схема которой приведена на рис.78.в, приложено напряжение U=300В. ВАХ сопротивлений заданы уравнениями: , , . Определить ток и напряжение на участке «аb».

Рис.78. Схема цепи

а

Решение:

По первому закону Кирхгофа.

А с учётом ВАХ резисторов имеем:

По второму закону Кирхгофа:

Получаем систему уравнений:

Решая систему уравнения, относительно получаем квадратное уравнение:

.

6.1.8. Туннельный диод, ВАХ которого изображена на рис.79б, соединён последовательно с источником ЭДС Е=1 и резистором сопротивлением R (рис.79а). Сопротивление R изменяется от 0 до ¥. Построить график зависимости тока I в цепи от сопротивления R.

а) б)

Рис.79. Схема цепи и ВАХ туннельного диода

а

Решение:

Ток в схеме определим по точкам пересечения ВАХ туннельного диода с нагрузочной прямой, построенной по уравнению Ud=E-IR, где Ud- напряжение на диоде.

Проведем ряд нагрузочных характеристик, и по точкам пересечения их с ВАХ диода определим рабочий режим.
Построим ряд нагрузочных характеристик по данным ВАХ диода:

1=1-0.005R1 → R1=0;

0, 8=1-0.003R2 → R2 =66 Ом;

0,1=1- 0.00373R3 → R3=240 Ом;

0,3=1-0.00175R4 → R4=400 Ом;

0,5=1-0.0005R5 → R5=1000 Ом.

При возрастании R от 0 до ∞ нагрузочная прямая поворачивается против часовой стрелки, меняя положение от вертикального до горизонтального. При < 0 < R < 240 Oм ток плавно снижается от 5 мА до1,5 мА.

При 240 < R < 1000 Ом для каждой нагрузочной прямой появляются три точки пересечения с ВАХ диода, поэтому получаются три участка на характеристике I=f(R); при R > 1000 Ом образуется одна точка пересечения от 1мА до 0. График I=f(R) представлен на рис. 79,г.

г)

6.1.9. Два одинаковых нелинейных сопротивления, ВАХ каждого из которых изображена на рис.80, соединены в одном случае последовательно, а в другом параллельно. К цепи приложено напряжение 200 В.

Определить токи.

Рис.80. ВАХ нелинейного элемента

а

Решение:

1.Два одинаковых нелинейных элемента соединены последовательно (рис.80.а).

Рис.80.а Схема цепи.

Рис.80.б.

Построим результирующую ВАХ, сложив напряжение (абсциссы) при одинаковых токах (ординатах).

U (I) =U1 (I) + U2 (I). (Рис 80,б).

По результирующей характеристике и известном напряжении сети 200В определим I = 5А , U1 = U2 = 100 B.

2.Два одинаковых нелинейных элемента соединены последовательно (рис 80.в).

Рис.80в. Схема цепи.

По ВАХ элементов определим токи I1 и I2 при U = 200 В.

I1 = 5 А ; I2 = 5 А.

По первому закону Кирхгофа

I = I1 + I2 = 10 А.

6.1.10.Построить входную ВАХ 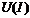схемы рис.81.а).

ВАХ нелинейных резистивных элементов HP1 и HP2 даны на рис.80.б),

R=5 Ом.

а)

б)

Рис.81. Схема цепи и ВАХ нелинейных элементов

а

Решение:

сначала строим ВАХ нелинейного резистивного элемента HP_э, эквивалентного параллельно соединенным HP1 и HP2.

Для этого складываем абсциссы ВАХ HP1 и HP2. В результате получим пунктирную кривую на рис. 82, б). HP_э соединен последовательно с резистором R, поэтому для получения результирующей ВАХ складываем ординаты ВАХ HP_э (пунктирная линия) и резистора сопротивлением R = 5 Ом (прямая линия). Красным (или жирным) вычерчена кривая, представляющая собой входную ВАХ.

6.1.11.Определить все токи методом эквивалентного генератора, если E1 = 18 В; Е2 = 6 В; J = 1 A; R1 = 3 Ом; R2 = 6 Ом. ВАХ нелинейного сопротивления задана на рис. 82.

а) б)

в) г)

Рис.82. Схема цепи и ВАХ нелинейного резистора

а

Решение:

Направление токов ветвей выберем произвольно (рис. 82.в ). Воспользуемся методом эквивалентного генератора. Исключим ветвь с Н.Э и определим напряжение на разомкнутых зажимах ab по формуле двух узлов.

U_{abxx =}

Закоротим источники E1 и E2 и найдем входное сопротивление относительно зажимов ab:

R_{bx = .}

Итак, параметры эквивалентного генератора:

E_экв = U_abxx = 8 В; R_вн = R_bx = 2 Ом.

Подключаем его к Н.Э, получаем схему (рис. 82,d)

a

Рис.82.d.

Рабочий режим Н.Э. найдем путем пересечения ВАХ с нагрузочной характеристикой нелинейного элемента, построенной по уравнению (м. А).

U_н.э = E_экв – I₃R_вн ;

U_н.э = 8 – 2I₃ .

Из графика находим I₃ = 3 А, U_ab = 2 В.

По второму закону Кирхгофа определим токи ветвей:

I₁ = = 5.33(А);

I₂ =

Проверка:

По первому закону Кирхгофа для узла a:

I₁ + I₂ - I₃ – J = 0.

5.33 – 1.33 – 3 – 1 = 0.

6.1.12.Рассчитать ток в нелинейном резисторе (рис.83,а) и мощность, выделяющуюся в нем. ВАХ резистора да на (рис. 83,б). Параметры цепи Е = 30В; J = 2A; R1 = 4 Ом ; R2= 1 Ом; R3 = 3 Ом ; R4= 2 Ом.

а) б)

Рис.83. Схема цепи и ВАХ нелинейного резистора

Рис.83.в

Решение:

Задачу решаем, используя метод эквивалентного генератора. Размыкая ветвь с нелинейным элементом. Схема приобретает вид (рис.84, г).

По формуле двух узлов определим напряжение между точками с и d.

Ucd = ;

Ucd = 15 В.

I₁ =

Рис.83.г

По второму закону Кирхгофа имеем :

U_abxx- JR₄+I₁R₁ = E ;

U_abxx = 22 В ;

E_экв = U_abxx = 22 В.

Далее, замыкаем источник ЭДС, размыкаем ветвь с источником тока и находим сопротивление относительно зажимов ab. (рис. 84, d)

Рис.83.д

R_bx = R₄ + ;

R_bx = R_вн = 4 Ом.

Параметры эквивалентного источника:

E _Экв = 22 В, R_вн = 4 Ом, (рис. 83,е).

Нагрузочная прямая

U_н.э = E _Экв – R_вн I ;

U_н.э = 22 – 4I.

Строим ее на графике ВАХ нелинейного элемента. Точка пересечения А дает рабочий режим цепи.

Потребляемая мощность в Н.Э:

P_н.э = U_ab I = 6 4 = 24 Вт.

Рис.83.г

6.1.13.Определить ток в нелинейном элементе, значения статического R_ст и дифференциального R_диф сопротивления при этом токе, если Е=20В, J=5А, R₁=3 Oм, R₂=2 Oм. Как изменится ток, Rст, Rдиф, если изменить полярность источника тока J. Схема цепи и ВАХ нелинейного элемента задана на рис.84.

а) б)

Рис.84. Схема цепи и ВАХ нелинейного элемента

Рис.84.в)

Решение:

Применим метод эквивалентного генератора. Разомкнем зажимы c и b и найдем напряжение U _bcxx (рис. 84,г).

U_ab = JR₂ = 5 2 = 10 В.

По второму закону Кирхгофа (рис. 85,г) запишем:

U_bcxx+ U_ab = E

U_bcxx = 10 В.

Рис.84.г)

Рис. 85, г

Разомкнем ветвь с источником тока, замкнем источник ЭДС и определим R_вн = R₁ + R₂ = 5 Ом.

Параметры эквивалентного источника E_экв = U_bcxx = 10 В, R_вн = 5 Ом.

Нагрузочная характеристика

U_н.э = E_экв - I R_вн ;

U_н.э = 10 – 5 I.

Строим прямую на графике ВАХ нелинейного элемента. Точка пересечения A дает рабочий режим.

Рис.84.д)

Итак, ток через нелинейный элемент

I = 1 А, U_н.э= 5 В.

Статическое сопротивление равно:

R_ст = = 5 Ом.

Для определения дифференциального сопротивления проведем касательную ВАХ через точку А. (пунктирная линия).

R _диф = ctgβ₁ = = -1 Ом.

Если изменить полярность источника,

E_экв = 30 В, R_вн= 5 Ом.

Нагрузочная характеристика нелинейного элемента:

U_н.э= 30 – 5I (см. рис. 84, в)

Рабочий режим – точка пересечения B.

I = 4,5 A, U_н.э= 7,5 B;

R_ст = = 1,666 Ом ; R _диф = ctgβ₂ = = 3 Ом.

6.1.14. Заменить нелинейный активный двухполюсник (рис.85.а) на эквивалентный и определить его параметры, ВАХ нелинейных элементов даны на рис.85.б, Е=30В, J=-1A.

а) б)

Рис.85. Схема цепи и ВАХ нелинейных элементов

Решение:

Строим зависимость токов I₁, J, I₂ в функции U_ab на основании следующих уравнений:

U _ab = E – U_н1 ; J = const ; U_ab = U _н2 (см. рис. 86, в) На основании первого закона Кирхгофа ток на входе двухполюсника I = J + I₂ –I₁ . Токи построены в функции одной и той же переменной U_ab, поэтому I(U_ab) = J(U_ab) + I₂(U_ab) – I₁(U_ab) (см. рис.86,в).

Эквивалентная схема приведена на рис.85,d.

Рис.85. в)

U_ab – U_э = E_э

U_ab = U_э + E_э

Значение E_э определяется точкой пересечения I = f(U_ab) и осью абсцисс E_э = 5 В.

U_н.э= U_ab - E_э

ВАХ нелинейного элемента получается, если I(U_ab) влево на E_э (рис.85,в).

Рис.85.д)

6.1.15. Нелинейный элемент имеет ВАХ, описываемую уравнением I=AU+bU³. Определить дифференциальное и статическое сопротивления элемента при напряжении: а) U=0 В, б) U=5 В.

Решение:

При U=0 В:

При U=5 В:

; ; ;

При U=0 В:

При U=5 В: