Тема 1. Числовые и степенные ряды.
Тема 1. Числовые и степенные ряды.
Основные свойства числовых рядов. Приближенное вычисление суммы числового ряда
Запишем основные сведения о числовых рядах:
 -
-  (1)
(1)
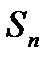 - это n-я частичная сумма ряда,
- это n-я частичная сумма ряда,
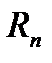 - это n-й частичный остаток ряда.
- это n-й частичный остаток ряда.
Числовой ряд (1) 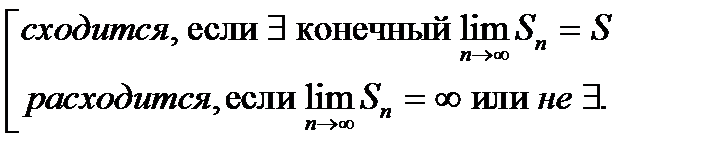
Число Sназывается суммой сходящегося ряда, это отражается равенством 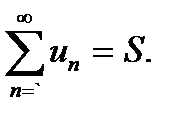
Очевидно, что любой ряд можно записать сложением его частичной суммы 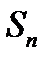 и соответствующего остатка
и соответствующего остатка 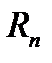 :
:
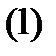

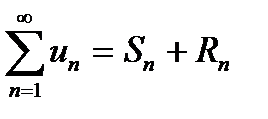 ;
;
Поэтому для сходящегося ряда верно, что  так как
так как 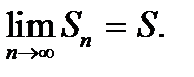
Оценки остатков некоторых сходящихся рядов. Приближенное вычисление суммы ряда
Рассмотрим сходящийся числовой ряд:
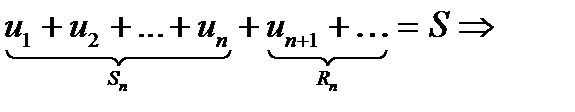

Так как  и
и 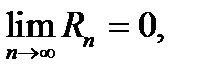 то при достаточно больших номерах n значения частичных сумм
то при достаточно больших номерах n значения частичных сумм  становится сколь угодно близкими к сумме ряда S , а значения соответствующих частичных остатков
становится сколь угодно близкими к сумме ряда S , а значения соответствующих частичных остатков 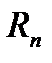 сколь угодно близкими к нулю. На основании этго можно вычислять приближенное значение суммы ряда S:
сколь угодно близкими к нулю. На основании этго можно вычислять приближенное значение суммы ряда S:
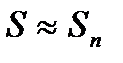 , погрешность этого приближенного равенства равна
, погрешность этого приближенного равенства равна 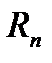 , она уменьшается с увеличением
, она уменьшается с увеличением 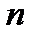 .
.
Задача «Вычислить сумму сходящегося числового ряда приближенно с наперед заданной точностью 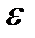 означает, что сумму ряда
означает, что сумму ряда 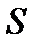 нужно заменить такой частичной суммой
нужно заменить такой частичной суммой 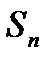 , чтобы соответствующий отбрасываемый остаток
, чтобы соответствующий отбрасываемый остаток 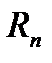 удовлетворял условию
удовлетворял условию  :
:
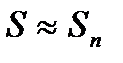 с точностью с точностью 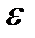 , если , если  (2) (2) |
Для практической работы по приближенной формуле (2) нужно иметь оценки для остатков сходящихся рядов.
Функциональные ряды. Определение. Понятие равномерной сходимости.
Функциональным называется ряд, членами которого являются функции, например одной переменной 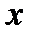 .
.
Общий вид:
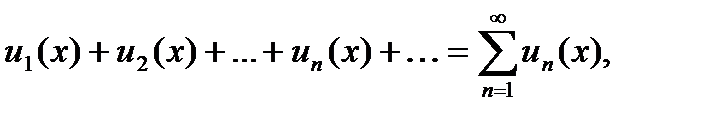 где
где 
Рассматривать ООФ функции  можно на
можно на  или
или 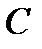 .
.
Примеры функциональных рядов:
1) 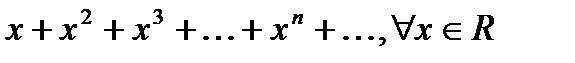 - степенной ряд
- степенной ряд
2) 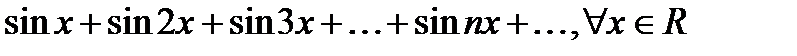 - пример тригонометрического ряда
- пример тригонометрического ряда
3) 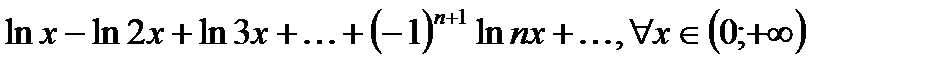
4) 
Точка сходимости функционального ряда 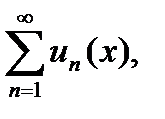 - это такое числовое значение
- это такое числовое значение  , при котором числовой ряд
, при котором числовой ряд 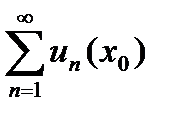 является сходящимся.
является сходящимся.
Точка расходимости функционального ряда 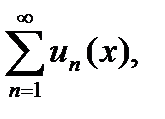 - это такое числовое значение
- это такое числовое значение  , при котором числовой ряд
, при котором числовой ряд  является расходящимся.
является расходящимся.
Область сходимости функционального ряда 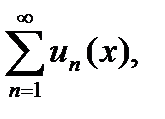 – это множество всех его точек сходимости.
– это множество всех его точек сходимости.
Область расходимости функционального ряда 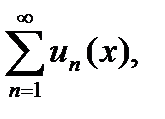 – это множество всех его точек расходимости.
– это множество всех его точек расходимости.
Пример:
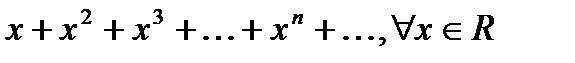

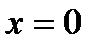 - точка сходимости, так как
- точка сходимости, так как 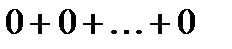 очевидно сходится.
очевидно сходится.
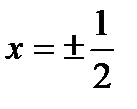 - точка сходимости, так как
- точка сходимости, так как 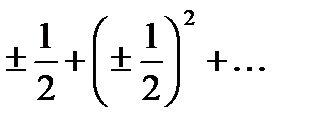 - сходится абсолютно.
- сходится абсолютно.
…
 - область сходимости данного ряда
- область сходимости данного ряда
 - область расходимости.
- область расходимости.
Сумма функционального ряда:
Рассмотрим функциональный ряд в области его сходимости:
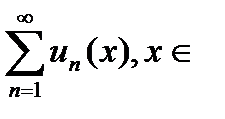 области сходимости ряда
области сходимости ряда 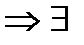 сумма ряда
сумма ряда
 области сходимости ряда, так что
области сходимости ряда, так что 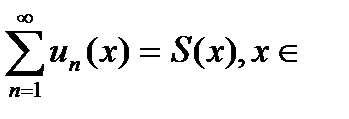 области сходимости.
области сходимости.
Пример:
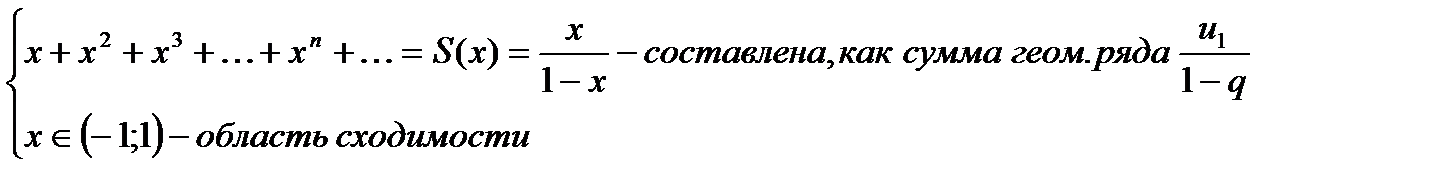
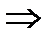
 , т.е. функция
, т.е. функция 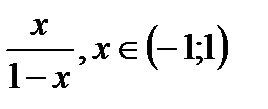 может быть представлена сходящимся степенным рядом.
может быть представлена сходящимся степенным рядом.
Связь суммы функционального ряда с его частичной суммой:
Рассмотрим сходящийся функциональный ряд:
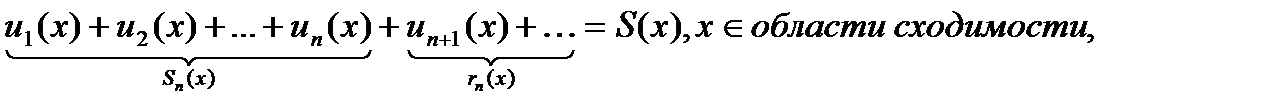
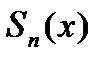 - п-я частичная сумма ряда,
- п-я частичная сумма ряда,
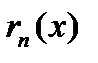 - п-ый частичный остаток
- п-ый частичный остаток
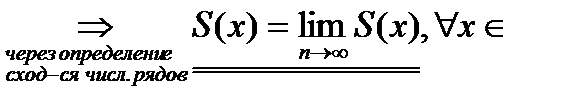 области сходимости
области сходимости
 области сходимости
области сходимости
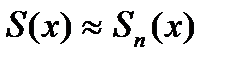 с погрешностью
с погрешностью 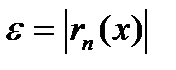 , при этом определить количество членов ряда n придется различным способом для различных х.
, при этом определить количество членов ряда n придется различным способом для различных х.
Степенные ряды
Степенным рядом называется функциональный ряд,членами которого являются степенные функции с натуральным показателем (или равным нулю).
Общий вид степенного ряда:
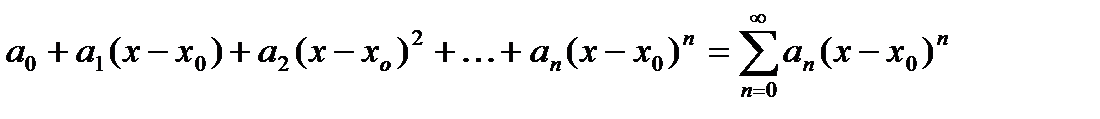
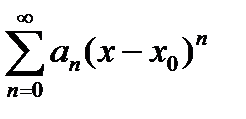 - степенной ряд по степеням разности
- степенной ряд по степеням разности 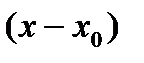 ,
,
где  - фиксированное число,
- фиксированное число,
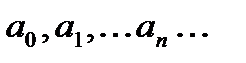 называются коэффициентами степенного ряда (
называются коэффициентами степенного ряда (  числа
числа 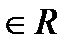 )
)
Частный случай, когда 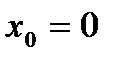 :
:
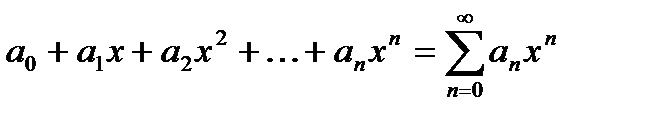 - степенной ряд по степеням
- степенной ряд по степеням 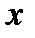 .
.
Теорема Абеля(важнейшая теорема для определения области сходимости степенного ряда):
Если ряд 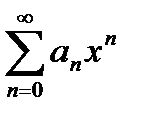 сходится в точке
сходится в точке 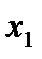 , то он сходится, причем абсолютно, при
, то он сходится, причем абсолютно, при 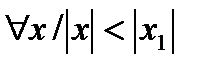 .
.
Если ряд 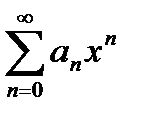 расходится в точке
расходится в точке 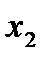 , то он расходится при
, то он расходится при 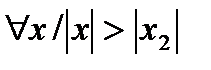 .
.
Иллюстрация к теореме Абеля:
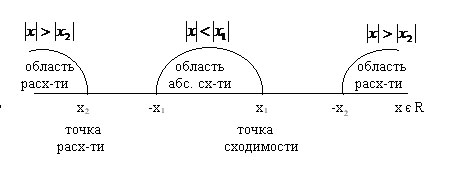
x=0 – тривиальная точка сходимости степенного ряда 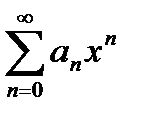
Понимание (обоснование) теоремы Абеля строится на использовании для знакоположительных числовых рядов признака сравнения в непредельной форме.
Следствие из теоремы Абеля:
R
R – радиус сходимости степенного ряда.
Таким образом для степенного ряда 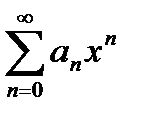 можно указать число
можно указать число 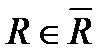 , называемое радиусом сходимости, такое что область абсолютной сходимости этого ряда представляет собой интервал
, называемое радиусом сходимости, такое что область абсолютной сходимости этого ряда представляет собой интервал 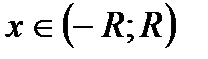 , симметричный относительно 0 и длины 2R;при этом на интервалах
, симметричный относительно 0 и длины 2R;при этом на интервалах 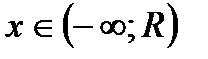 и
и 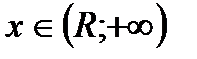 ряд всегда расходится; точки
ряд всегда расходится; точки 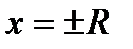 (точки концов этих интервалов) нужно исследовать для каждого ряда индивидуально.
(точки концов этих интервалов) нужно исследовать для каждого ряда индивидуально.
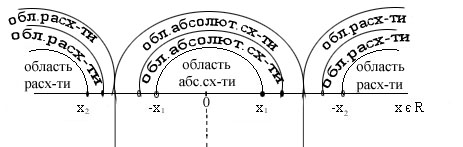
Схема области сходимости/расходимости степенного ряда 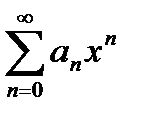 (теоретическая):
(теоретическая):
Аналогично получается теоретическая схема сходимости/расходимости общего степенного ряда 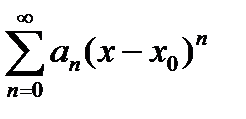
 - центр области сходимости.
- центр области сходимости.
Радиус сходимости R может оказаться:
1. R=0
2. R=число
3. R= 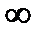
Примеры:
Определить область сходимости и область расходимости следующих степенных рядов:
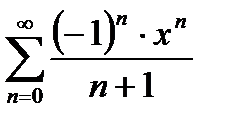
Так как степенной ряд по степеням х, то схема его области сходимости имеет вид:
Для вычисления R применим признак Даламбера к ряду, составленному из модулей членов данного ряда:
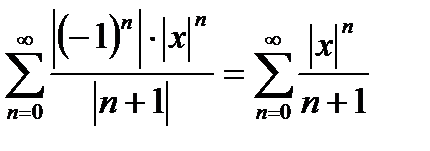
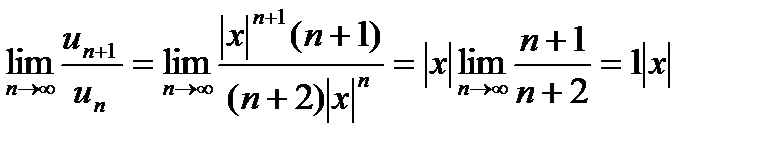
По признаку Даламбера:
Ряд из модулей 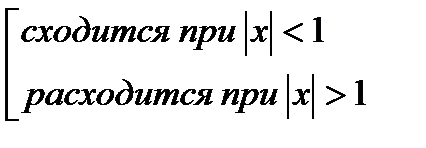
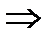 исходный степенной ряд сходится абсолютно, только при
исходный степенной ряд сходится абсолютно, только при 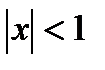 (признак абсолютной сходимости).
(признак абсолютной сходимости).
Сравнивая получившиеся результаты с теоретической схемой, заключаем, что:
1. R=1, так как исходный ряд сходится абсолютно только при 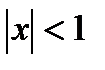
2. при 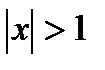 абсолютной сходимости быть не может, так как расходится ряд из модулей; сравнивая со схемой, получаем, что
абсолютной сходимости быть не может, так как расходится ряд из модулей; сравнивая со схемой, получаем, что 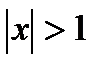 - это область расходимости.
- это область расходимости.
Дополнительно исследуем сходимость исходного ряда при 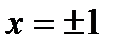 :
:
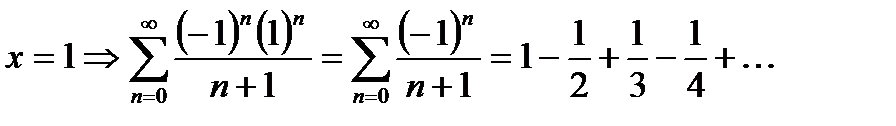 - ряд Лейбница, сходится условно.
- ряд Лейбница, сходится условно.
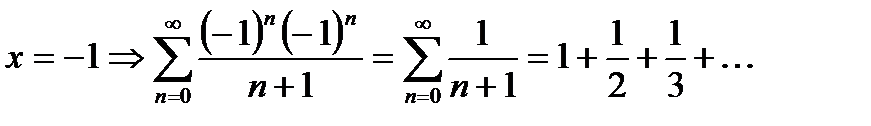 - гармонический ряд, расходится.
- гармонический ряд, расходится.
Окончательная схема области сходимости/расходимости исходного ряда:
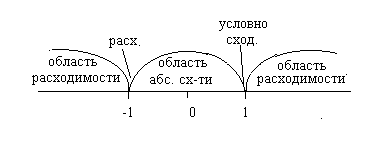
Ответ: 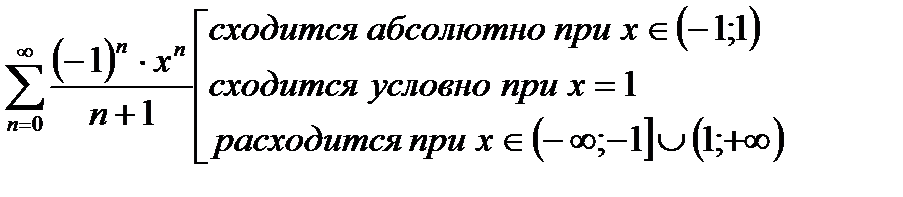
Замечание: если признак Даламбера или радикальный признак Коши применить к степенному ряду в общем виде 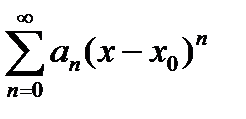 , то можно получить теоретические формулы для нахождения радиуса сходимости R.
, то можно получить теоретические формулы для нахождения радиуса сходимости R.
Ряд из модулей: 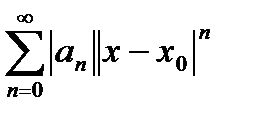
Признак Даламбера: 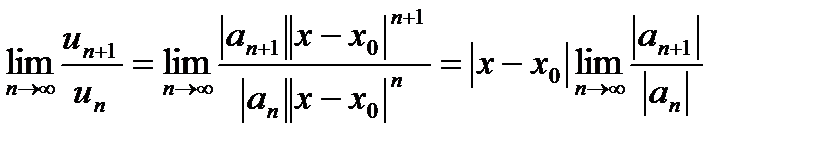
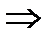 ряд из модулей сходится, если
ряд из модулей сходится, если 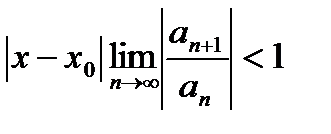 или расходится, если
или расходится, если 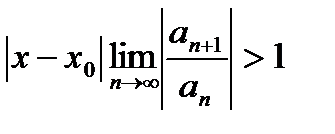 .
.
Теоретическая схема области сходимости/расходимости:
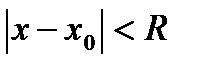
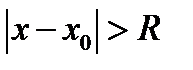
2R
Сравнивая результаты, полученные по признаку Даламбера с теоретической схемой, заключаем, что R нужно находить из условий: 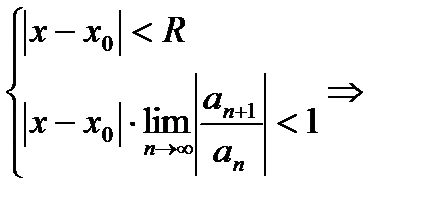
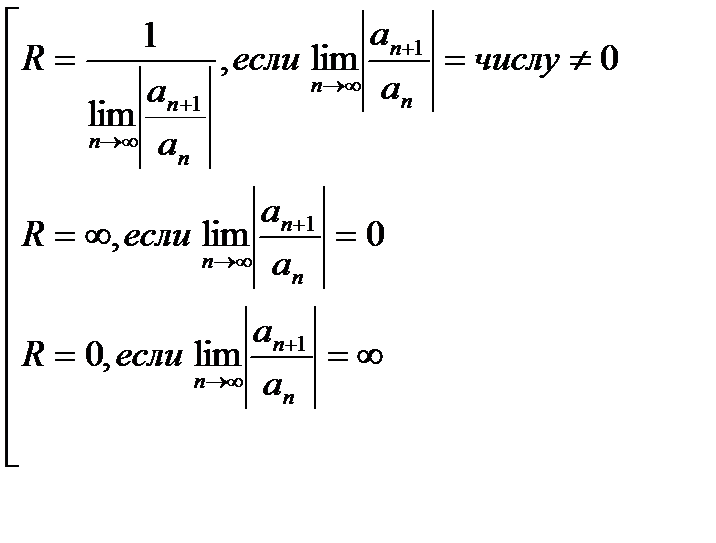
Однако выведенные формулы для R не очень удобны на практике, так как:
1. Для их применения нужно анализировать значение 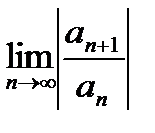
2. Для вычисления 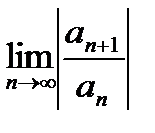 нужно, чтобы все
нужно, чтобы все 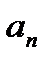 были отличны от нуля.
были отличны от нуля.
Например, для 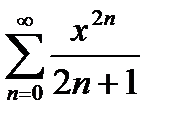 применять формулы для R нельзя, так как все
применять формулы для R нельзя, так как все 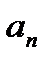 (нечетные) равны 0.
(нечетные) равны 0.
Ряды Тейлора и Маклорена.
Рассматриваем функцию  - дифференцируемая сколько угодно раз в точке
- дифференцируемая сколько угодно раз в точке  и некоторой ее окрестности
и некоторой ее окрестности  .
.
Рядом Тейлора для функции  в точке
в точке  называется следующий числовой ряд:
называется следующий числовой ряд:
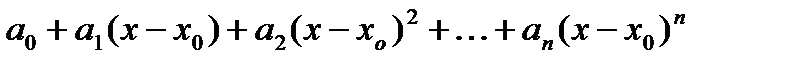 , (1)
, (1)
в котором коэффициенты 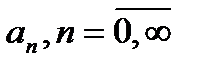 вычислены через функцию
вычислены через функцию  по следующим формулам:
по следующим формулам:
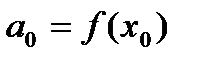 ,
,
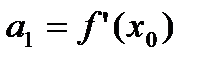 ,
,
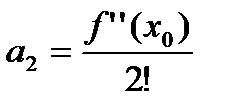 .
.
…
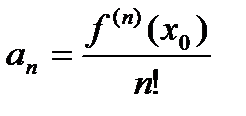
Рядом Маклорена для функции  называется частный случай ее ряда Тейлора в точке
называется частный случай ее ряда Тейлора в точке  =0:
=0:
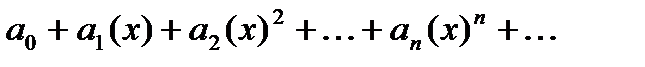 (2)
(2)
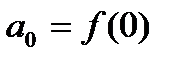 ,
,
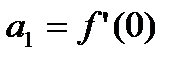 ,
,
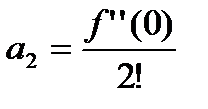 .
.
…
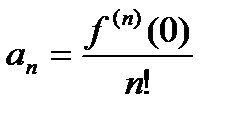
Название для рядов (1) и (2) сохраняются независимо от их сходимости/расходимости и даже в случае, если ряды сходятся не к функции  .
.
Если ряд Тейлора (Маклорена) сходится в некоторой области к функции  , то справедливо равенство:
, то справедливо равенство:
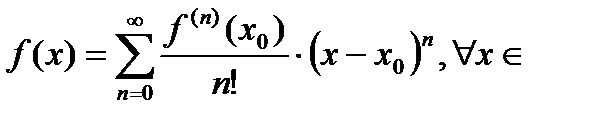 области сходимости ряда Тейлора. (3)
области сходимости ряда Тейлора. (3)
В этом случае это равенство называется разложением функции в ряд Тейлора в точке  .
.
Замечание: так как ряд Тейлора – это есть степенной ряд по степеням 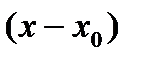 , его область сходимости записывается неравенством
, его область сходимости записывается неравенством 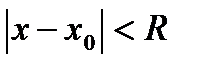 , R – радиус сходимости. Так как это неравенство описывает
, R – радиус сходимости. Так как это неравенство описывает 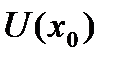 , то разложение функции
, то разложение функции  в ее ряд Тейлора справедливо в точке
в ее ряд Тейлора справедливо в точке  и некоторой ее окрестности
и некоторой ее окрестности 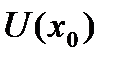 .
.
Пример:
Составить разложение функции 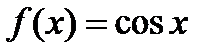 в ряд Тейлора в точке
в ряд Тейлора в точке 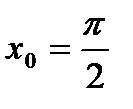 . Найти окрестность
. Найти окрестность 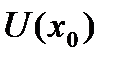 , в которой составленный ряд находится.
, в которой составленный ряд находится.
Решение:
Хотим получить следующее разложение:
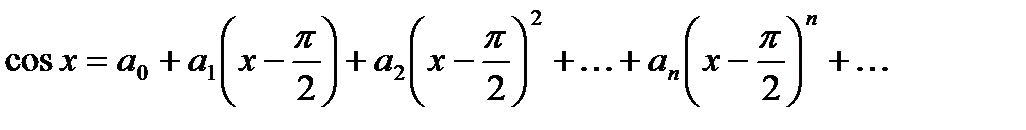 ,
,
где 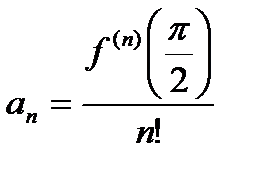 .
.
Разложение должно быть верно по окрестности 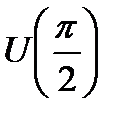 , т.е. при
, т.е. при 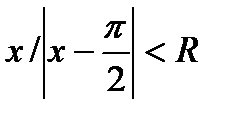 .
.
1. Вычислим коэффициенты Тейлора:
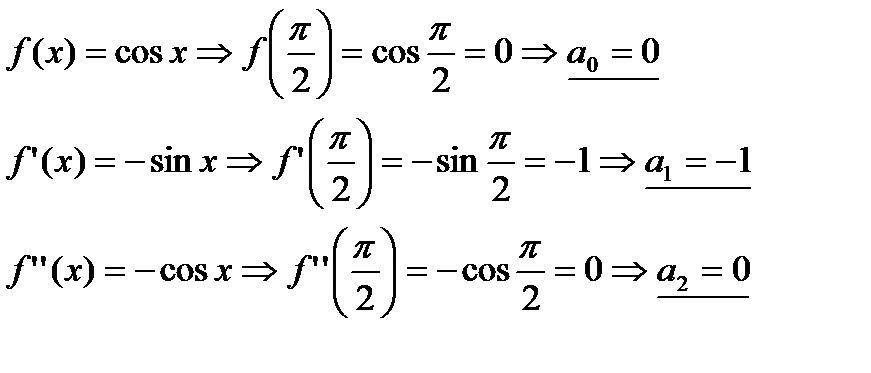
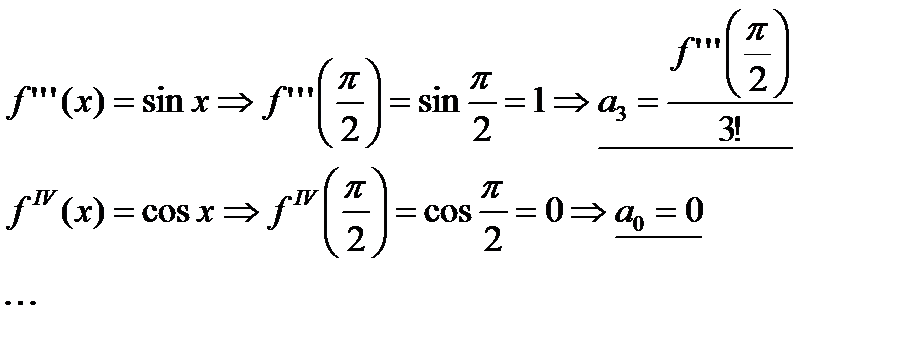

Составляем ряд Тейлора:
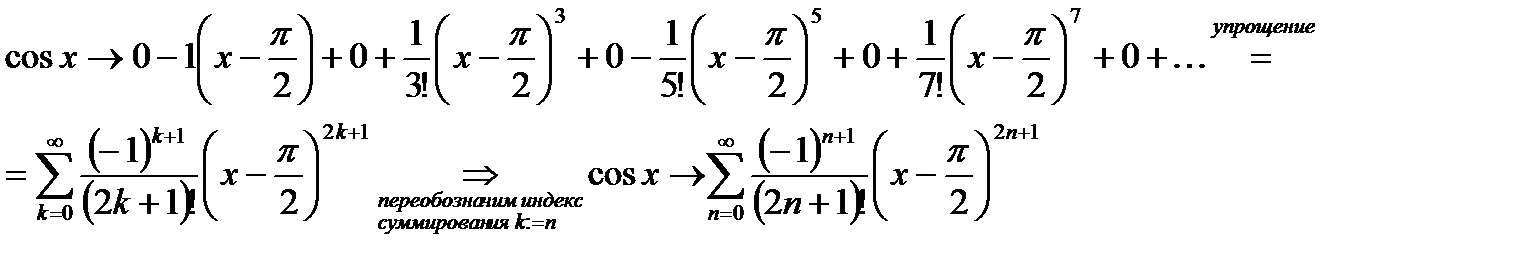
2. Зная, что составленный степенной ряд сходится абсолютно при 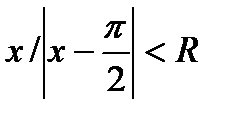 , вычислим R, применяя признак Даламбера к ряду из модулей:
, вычислим R, применяя признак Даламбера к ряду из модулей:
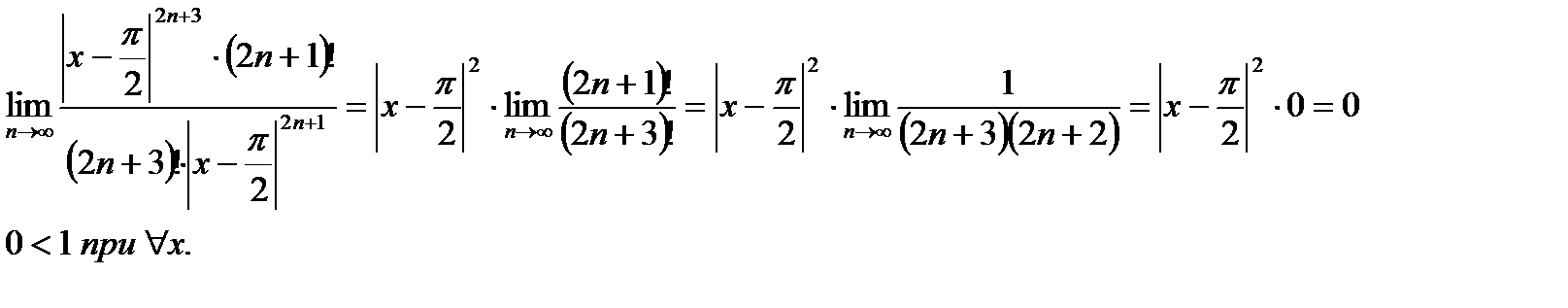
 составленный степенной ряд сходится при
составленный степенной ряд сходится при 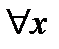 и его
и его 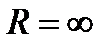 .
.
3. Составленный ряд сходится при 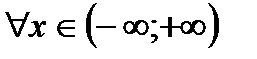 , но остается недоказанным, что его сумма
, но остается недоказанным, что его сумма 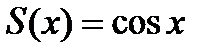 .
.
Поэтому ответ по задаче остается неполным.
Ответ: 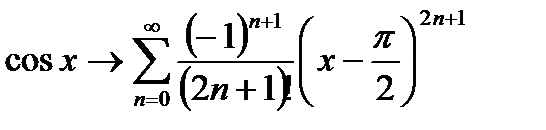 сходится абсолютно при
сходится абсолютно при 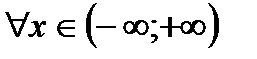 .
.
Остаточный член ряда Тейлора в форме Лагранжа:
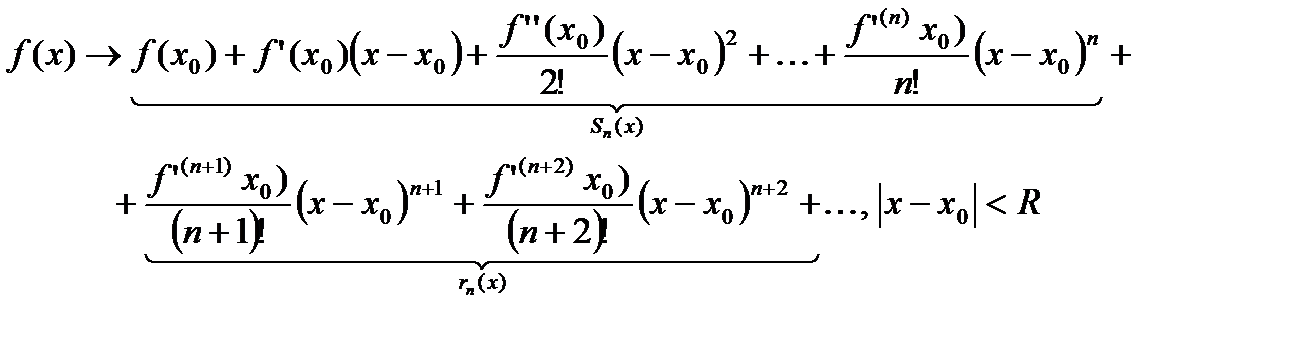
Можно показать, что:
1. Остаток ряда Тейлора записывается в нескольких конечных формах, наиболее распространенной из этих форм является форма Лагранжа:
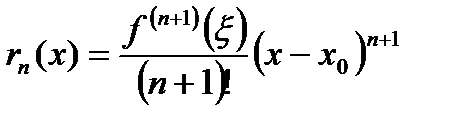 , где
, где 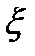 - некоторая фиксированная точка между точкой
- некоторая фиксированная точка между точкой  и точкой х.
и точкой х.
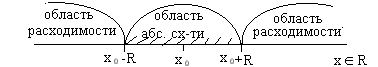
2R
2. Достаточным условием для того, чтобы составленный ряд Тейлора сходился именно к той функции, для которой он составлялся, является условие 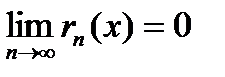 , где
, где 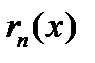 записано в форме Лагранжа.
записано в форме Лагранжа.
Пример:
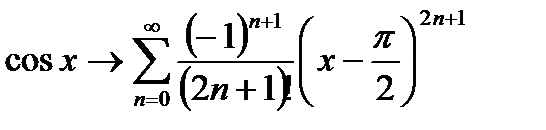 ,
, 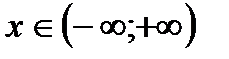
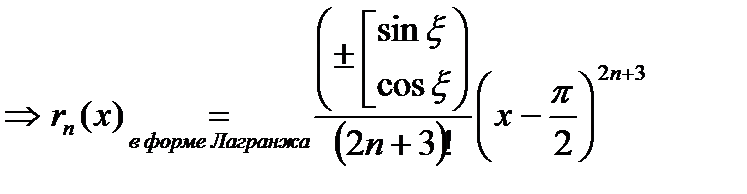 , где
, где 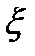 - некоторая фиксированная точка слева или справа от
- некоторая фиксированная точка слева или справа от  (между х и
(между х и  ).
).
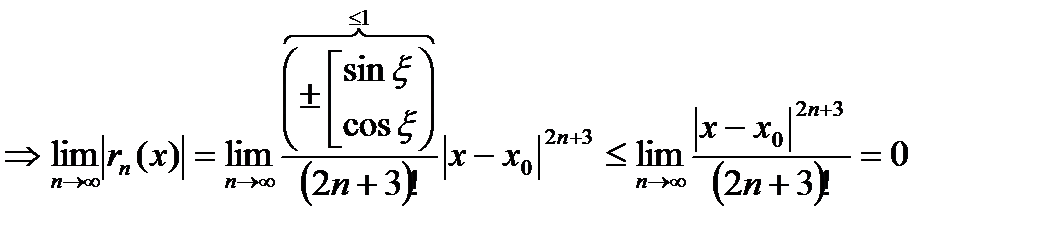 , так как
, так как 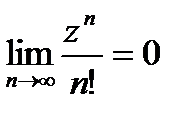 при
при 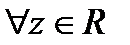 , т.е. степенная функция с любым основанием при увеличении ее основания растет медленнее, чем факторная ее показателя (будет обосновано позже).
, т.е. степенная функция с любым основанием при увеличении ее основания растет медленнее, чем факторная ее показателя (будет обосновано позже).
Таким образом, 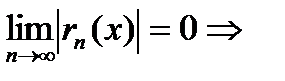 ряд сходится,
ряд сходится,
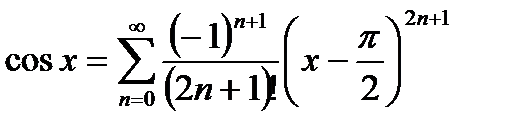 - это равенство называется разложением
- это равенство называется разложением 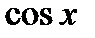 в ряд Тейлора в точке
в ряд Тейлора в точке 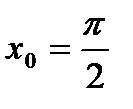 (или по степени
(или по степени 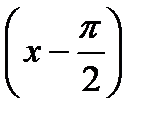 ).
).
Замечания к разложениям функций в ряды Тейлора:
1. Необходимым условием для разложения функции в ряд Тейлора является существование и непрерывность в точке  и
и 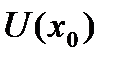 производных любого порядка, т.е. функция
производных любого порядка, т.е. функция  должна быть непрерывно дифференцируемой бесконечное количество раз в точке
должна быть непрерывно дифференцируемой бесконечное количество раз в точке  и
и 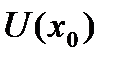 .
.
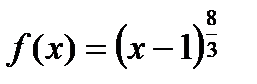 - такую функцию в точке
- такую функцию в точке 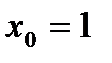 в ряд Тейлора разложить нельзя, так как
в ряд Тейлора разложить нельзя, так как 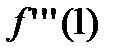 не
не 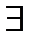 ( но в точке
( но в точке 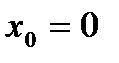 и других точках
и других точках  - можно)
- можно)
 разложение функции в степенной ряд в точке
разложение функции в степенной ряд в точке  это локальная процедура, так как она выполняется только по некоторой окрестности
это локальная процедура, так как она выполняется только по некоторой окрестности 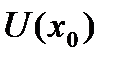
2. Если  в точке
в точке  разлагается в степенной ряд, то это разложение является единственным и совпадает с ее разложением в ряд Маклорена.
разлагается в степенной ряд, то это разложение является единственным и совпадает с ее разложением в ряд Маклорена.
Доказательство:
Пусть  имеет разложение в ряд по степеням
имеет разложение в ряд по степеням 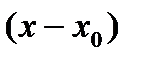 :
:
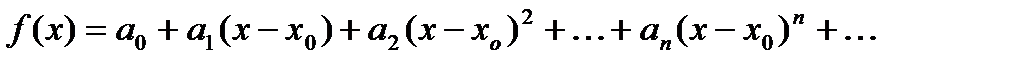 ,
, 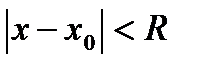
Это равенство справедливо при всех х из промежутка сходимости, следовательно, справедливо при  ,
,  при
при 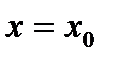
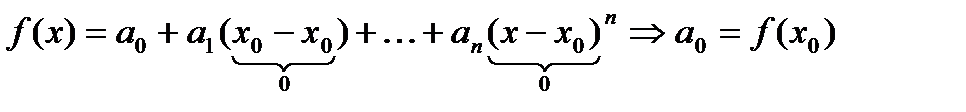
Так как степенные ряды можно почленно дифференцировать, то справедливо равенство:
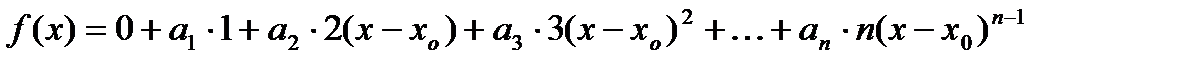 ,
, 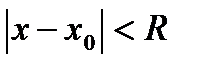
 при
при 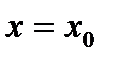
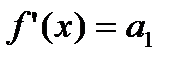 .
.
Аналогично, повторяя дифференцирование разложения в ряд и полагая 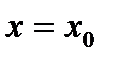 , получим
, получим 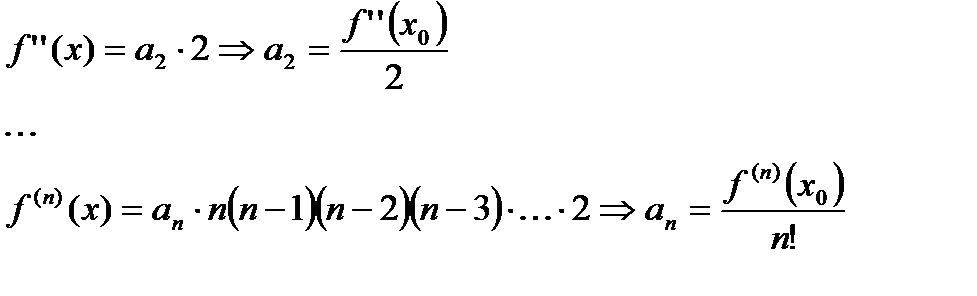
Для произвольно взятого разложения функции  в степенной ряд доказали, что его коэффициенты неизбежно совпадают с коэффициентами Тейлора
в степенной ряд доказали, что его коэффициенты неизбежно совпадают с коэффициентами Тейлора 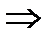 разложение
разложение  в степенной ряд единственно и совпадает с разложением Тейлора.
в степенной ряд единственно и совпадает с разложением Тейлора.
3. Достаточным условием для того, чтобы ряд Тейлора сходился к  является условие:
является условие:
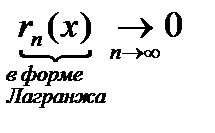
Обоснование этого факта для конкретной функции  является, как правило, затруднительным, поэтому в приложениях стараются получить разложение функции в степенной ряд, используя так называемые стандартные разложения в ряд Маклорена некоторых элементарных функций. При этом и промежуток сходимости и сумма ряда получаются автоматически.
является, как правило, затруднительным, поэтому в приложениях стараются получить разложение функции в степенной ряд, используя так называемые стандартные разложения в ряд Маклорена некоторых элементарных функций. При этом и промежуток сходимости и сумма ряда получаются автоматически.
Тема 1. Числовые и степенные ряды.
