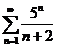Линейные неоднородные ДУ 2 порядка с постоянными коэффициентами со специальной правой частью.
Рассм. ДУ
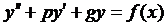
Общее решение такого уравнения:
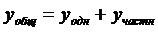 , где
, где 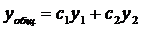
ФСР 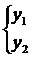 - уже рассматривали
- уже рассматривали
Укажем метод нахождения частного решения неоднородного уравнения
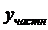 , если f(x) имеет специальный вид.
, если f(x) имеет специальный вид.
 Рассмотрим следующие случаи:
Рассмотрим следующие случаи:
I. 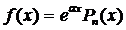 ,где
,где  - многочлен степени n.
- многочлен степени n.
а) 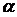 - не корень характеристического уравнения
- не корень характеристического уравнения 

 , где
, где 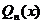 - многочлен степени n с неопределенными буквенными коэффициентами. Подставим
- многочлен степени n с неопределенными буквенными коэффициентами. Подставим 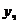 в ДУ и сравнив коэффициенты при одинаковых степенях найдём все буквы.
в ДУ и сравнив коэффициенты при одинаковых степенях найдём все буквы.
б) 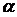 - корень характеристического уравнения кратности 1
- корень характеристического уравнения кратности 1 

в) 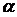 - корень характеристического уравнения кратности 2
- корень характеристического уравнения кратности 2 
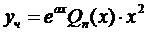
II. .  ,где M,Nчисла
,где M,Nчисла
a)  не корень характеристического уравнения
не корень характеристического уравнения 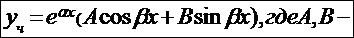 неопределенные коэффициенты.Подставив
неопределенные коэффициенты.Подставив  в ДУ и приравняв коэффициенты при
в ДУ и приравняв коэффициенты при 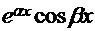
 находим А и В
находим А и В
б)  корень характеристического уравнения кратности 1
корень характеристического уравнения кратности 1 
 |
Замечание : Если в правой части 
 есть только
есть только  или
или 
в частном решении  должны быть и sin и cos , т.е тригонометрия должна быть полной.
должны быть и sin и cos , т.е тригонометрия должна быть полной.
III. . 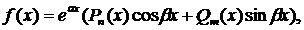
Где 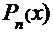 ,
,  -многочлены степеней m и n
-многочлены степеней m и n
a)  не корень характеристического уравнения
не корень характеристического уравнения 
 многочлены степени к с неопределенными коэффициентами
многочлены степени к с неопределенными коэффициентами
б)  корень характеристического уравнения
корень характеристического уравнения 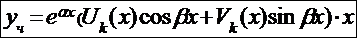
Метод вариации
Рассмотрим ДУ: 
Где правая часть f(x) произвольного вида (необязательно специального).
Общее решение соответствующего однородного уравнения:
 , где
, где 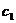 и
и 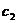 - произвольные const,
- произвольные const, 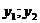 - ФСР.
- ФСР.
Будем варьировать 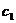 и
и 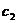 и считать, что
и считать, что 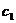 и
и 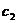 зависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде:
зависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде:
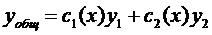
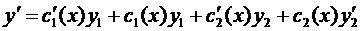
 (*)
(*)


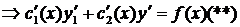
объединим 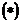 и
и  в систему
в систему
 - эта система для нахождения
- эта система для нахождения 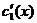 и
и 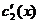 имеет единственное решение, т.к определитель системы
имеет единственное решение, т.к определитель системы  ,
,
для системы 2-х ЛНЗ надежнее решать систему по формулам Крамера
 , где
, где 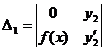
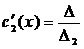 , где
, где 
решая систему получим 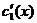 и
и 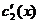 , проинтегрируем полученные функции по переменной х.
, проинтегрируем полученные функции по переменной х.
 - проинтегрируем по х
- проинтегрируем по х
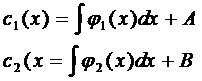 , где А и В – константы интегрирования
, где А и В – константы интегрирования
Таким образом общее решение неоднородного уравнения:

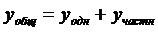
Пример:
1) 
Решение систем линейных ДУ 1 порядка с постоянными коэффициентами способом подстановки
Рассмотрим систему ДУ
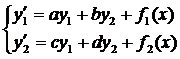 , где a,b,c,d – числа.
, где a,b,c,d – числа.
 - искомая функция
- искомая функция  - функции переменной х
- функции переменной х
продифференцируем по переменной х первое уравнение системы:
Дифф.(1) 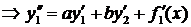
Подставим из (2) 

подставим из (1) 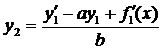
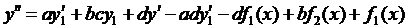
перенесем слагаемые с  и
и  налево
налево

получим линейное неоднородное ДУ 2 порядка с постоянными коэффициентами. Решая это уравнение получим  , продифференцируем
, продифференцируем  и найдём
и найдём 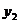 .
.
Пример:
1)  начальные условия:
начальные условия: 
РАЗДЕЛ: «Ряды»
Числовые ряды
Определение:Рассмотрим бесконечную числовую последовательность:
 числовым рядом называется выражение
числовым рядом называется выражение  , где
, где  – общий член ряда.
– общий член ряда.
Пример:
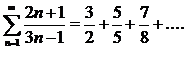 -знакоположительный ряд
-знакоположительный ряд
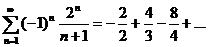 -знакочередующийся ряд
-знакочередующийся ряд
Последовательность  , где
, где  ;
; 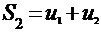 ;
; 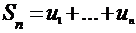 - последовательность частичных сумм ряда.
- последовательность частичных сумм ряда.
Каждая частичная сумма содержит конечное число слагаемых.
Числовой ряд 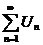 называется сходящимся, если существует конечный
называется сходящимся, если существует конечный
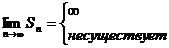 , то ряд называется расходящимся и суммы S не имеют.
, то ряд называется расходящимся и суммы S не имеют.
1)Рассмотрим ряд из членов геометрической прогрессии.
 , где n – частичная сумма ряда
, где n – частичная сумма ряда  - сумма n первых членов геометрической прогрессии.
- сумма n первых членов геометрической прогрессии.
Рассмотрим 3 случая:
1)  геометрическая прогрессия убывающая.
геометрическая прогрессия убывающая.
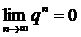
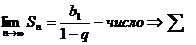 сходится и имеет сумму
сходится и имеет сумму 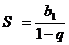
2) 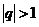

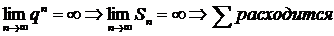
3) 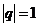
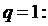
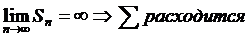

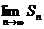 = не существует – ряд расходится.
= не существует – ряд расходится.
Вывод: ряд из членов геометрической прогрессии сходится если  и расходится
и расходится 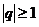

Элементарные свойства рядов
1) Если  (1) сходится и имеет сумму S, то
(1) сходится и имеет сумму S, то  (2) тоже сходится, и имеет сумму CS, где С-const.
(2) тоже сходится, и имеет сумму CS, где С-const.
Доказательство:Пусть  , n– ая частичная сумма 1 ряда.
, n– ая частичная сумма 1 ряда.
 , n–ая частичная сумма 2 ряда.
, n–ая частичная сумма 2 ряда.
Т.к 1 ряд сходится, то 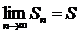 .
.
Рассмотрим 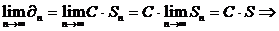 (2) ряд сходится.
(2) ряд сходится.
Конец доказательства.
2) Если 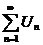 (1) сходится с суммой S1, и
(1) сходится с суммой S1, и 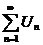 (2) сходится с суммой S2.
(2) сходится с суммой S2. 
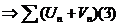 тоже сходится с суммой
тоже сходится с суммой 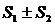 .
.
Доказательство:
Обозначим  - n – частичная сумма 1 ряда.
- n – частичная сумма 1 ряда.
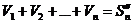 - n – частичная сумма 2 ряда.
- n – частичная сумма 2 ряда.
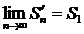

Рассмотрим n-ую частичную сумму ряда


 и сумма
и сумма  .
.
Конец доказательства.
3) Любой ряд может быть представлен в виде:
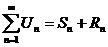 , где
, где  - n – частичная сумма
- n – частичная сумма
 - n – остаток ряда.
- n – остаток ряда.
n – остаток ряда  тоже является рядом.
тоже является рядом.
Если  , то и его остаток
, то и его остаток 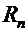 тоже сходится.
тоже сходится.
Доказательство: доказательство этого факта следует из того, что сумма ряда и сумма его остатка отличаются друг от друга на конечное число cлагаемых.
Конец доказательства.
Следствие: на сходимость ряда не влияет отбрасывание или приписывание в начало ряда конечного числа членов, например: 1+3+9+27+…
Дописывание : 1/9+1/3+1+3+9+27+.. отбрасывание: 1+3+5+7+9+11
4)Если 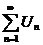 сходится с суммой S
сходится с суммой S 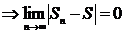 .
.
Общий вывод:на практике необязательно выяснять сходимость ряда по определению (вычисляя сумму S). Достаточно просто знать сходится этот ряд или расходится, поэтому, основное место в теории рядов занимают теоремы – признаки сходимости, которые позволяют исследовать ряд на сходимость, не вычисляя его суммы.
Признаки сходимости
Необходимый признак сходимости:
Если 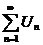 сходится, то общий член
сходится, то общий член 
Доказательство: Пусть  - n – частичная сумма.
- n – частичная сумма.
 - число.
- число.
При  ,
, 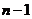 тоже
тоже 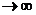 и
и  - n-1 – частичная сумма.
- n-1 – частичная сумма.
Она имеет предел  .
.
Т.к 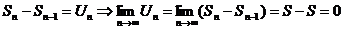
 конец доказательства.
конец доказательства.
Необходимый признак сходимости неудобен на практике, т.к по поведению общего члена Un на бесконечности нельзя судить о сходимости ряда.
На практике удобно пользоваться достаточным признаком расходимости ряда:
Если  не стремится к 0 при
не стремится к 0 при 

Примеры:
1) 
2)