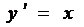Дифференциальные уравнения 1 порядка
Введение
При изучении некоторых явлений часто возникает ситуация, когда процесс не удаётся описать с помощью уравнения y=f(x) или F(x;y)=0. Помимо переменной х и неизвестной функции , в уравнение входит производная этой функции.
Определение:Уравнение, связывающее переменную х, неизвестную функцию y(x) и её производные называется дифференциальным уравнением. В общем виде дифференциальное уравнение выглядит так:
F(x;y(x); 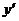 ;
; 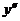 ;...;y(n))=0
;...;y(n))=0
Определение:Порядком дифференциального уравнения называется порядок входящей в него старшей производной.
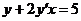 – дифференциальное уравнение 1 порядка
– дифференциальное уравнение 1 порядка
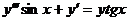 – дифференциальное уравнение 3 порядка
– дифференциальное уравнение 3 порядка
Определение:Решением дифференциального уравнения является функция, которая при подстановке в уравнение обращает его в тождество.
Дифференциальные уравнения 1 порядка
Определение: Уравнение вида 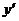 =f(x;y) или F(x;y;
=f(x;y) или F(x;y; 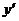 )=0 называется дифференциальным уравнением 1 порядка.
)=0 называется дифференциальным уравнением 1 порядка.
Определение:Общим решением дифференциального уравнения 1 порядка называется функция y=γ(x;c), где (с –const), которая при подстановке в уравнение обращает его в тождество. Геометрически на плоскости общим решением соответствует семейство интегральных кривых, зависящих от параметра с.
|
Примеры:
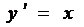
Теорема о существовании единственности решения дифференциального уравнения 1 порядка
Дано дифференциальное уравнение 1 порядка 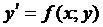 и функция f(x;y) непрерывна вместе с частными производными в некоторой области D плоскости XOY, тогда через точку М0(х0;y0)
и функция f(x;y) непрерывна вместе с частными производными в некоторой области D плоскости XOY, тогда через точку М0(х0;y0) 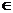 D проходит единственная кривая соответствующая частному решению дифференциального уравнения соответствующему начальному условию y(x0)=y0
D проходит единственная кривая соответствующая частному решению дифференциального уравнения соответствующему начальному условию y(x0)=y0
Через точку плоскости с данными координатами проходит 1 интегральная кривая.
Если не удаётся получить общее решение дифференциального уравнения 1 порядка в явном виде, т.е 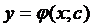 , то его можно получить в неявном виде:
, то его можно получить в неявном виде:
F(x; y; c) =0 – неявный вид
Общее решение в таком виде называется общим интегралом дифференциального уравнения.
По отношению к дифференциальному уравнению 1 порядка ставится 2 задачи:
1)Найти общее решение (общий интеграл)
2)Найти частное решение (частный интеграл) удовлетворяющее заданному начальному условию. Эту задачу называют задачей Коши для дифференциального уравнения.
Уравнения Бернулли

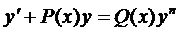 , где
, где 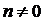 ;1
;1
Решаются такие уравнения так же как и линейные
Замена 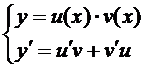

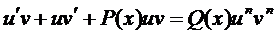
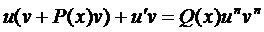

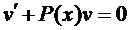
Явно 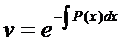
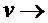
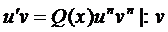
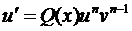 - дифференциальное уравнение с разделяющимися переменными.
- дифференциальное уравнение с разделяющимися переменными.
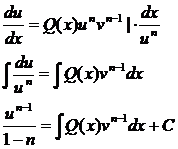
выразим явно u и найдём общее решение 
Примеры:
1) 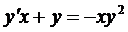
Теорема Коши.
Если функция 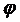 в (*) непрерывна вместе с частными производными:
в (*) непрерывна вместе с частными производными:
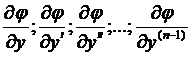 в области содержащей значения
в области содержащей значения
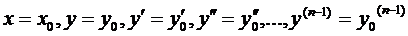 , то существует единственное решение дифференциального уравнения
, то существует единственное решение дифференциального уравнения 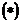 удовлетворяющее начальным условиям:
удовлетворяющее начальным условиям:
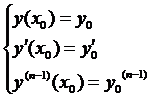
Замечание: для дифференциальных уравнений 2 порядка 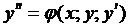
начальные условия имеют вид:
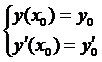
Решить дифференциальное уравнение порядка n означает:
1)Найти общее решение (общий интеграл)
2)Найти частное решение (частный интеграл), удовлетворяющее заданным условиям.
Определение:Общим решением дифференциального уравнения 2 порядка
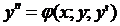 является функция
является функция 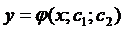 , такая что:
, такая что:
1) при любых значениях с1 и с2 эта функция – решение.
2) каковы бы ни были начальные условия на области, в которой выполняется теорема Коши всегда можно подобрать значения с1 и с2 удовлетворяющие начальным условиям.
Определение:Частным решением дифференциального уравнения 2 порядка является решение, при конкретных значениях с1 и с2.
Замечание: общее решение дифференциального уравнения 2 порядка может быть получено в неявном виде: 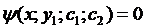
Линейные неоднородные ДУ
Это уравнения вида: 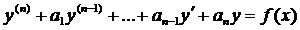
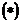
Теорема об общем решении ДУ:Общее решение ДУ(*) имеет вид:
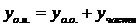 , где
, где 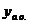 - общее решение соответствующего однородного уравнения.
- общее решение соответствующего однородного уравнения.
Доказательство: подставим 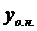 в
в 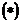
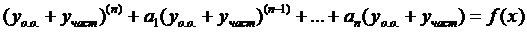
раскроем скобки и перегруппируемся:
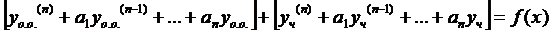 (верно)
(верно)
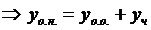
Если даны н.у
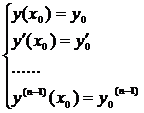
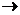 нужно показать, что все константы находятся однозначно
нужно показать, что все константы находятся однозначно
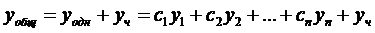 , где ФСР
, где ФСР 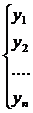
Продифференцируем 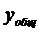 нужное количество раз и подставим н.у
нужное количество раз и подставим н.у
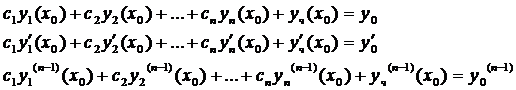
получим систему n-линейных уравнений с n неизвестными 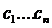 . Определитель этой системы
. Определитель этой системы 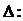
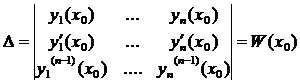 - определитель Вронского системы функций
- определитель Вронского системы функций 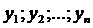 .
.
Т.к 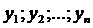 - ФСР
- ФСР 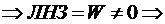 линейная система имеет единственное решение и все константы находятся однозначно.
линейная система имеет единственное решение и все константы находятся однозначно.
Конец доказательства.
Замечание:Общее решение соответствующего однородного уравнения
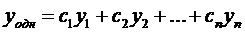 - линейная комбинация ФСР – известно
- линейная комбинация ФСР – известно
Основная трудность нахождения yч – решения неоднородного уравнения.
Метод вариации
Рассмотрим ДУ: 
Где правая часть f(x) произвольного вида (необязательно специального).
Общее решение соответствующего однородного уравнения:
 , где
, где 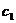 и
и 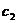 - произвольные const,
- произвольные const, 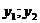 - ФСР.
- ФСР.
Будем варьировать 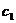 и
и 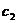 и считать, что
и считать, что 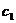 и
и 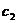 зависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде:
зависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде:
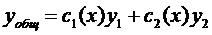
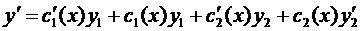
 (*)
(*)


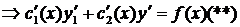
объединим 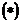 и
и  в систему
в систему
 - эта система для нахождения
- эта система для нахождения 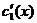 и
и 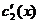 имеет единственное решение, т.к определитель системы
имеет единственное решение, т.к определитель системы  ,
,
для системы 2-х ЛНЗ надежнее решать систему по формулам Крамера
 , где
, где 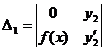
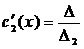 , где
, где 
решая систему получим 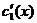 и
и 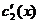 , проинтегрируем полученные функции по переменной х.
, проинтегрируем полученные функции по переменной х.
 - проинтегрируем по х
- проинтегрируем по х
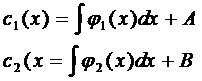 , где А и В – константы интегрирования
, где А и В – константы интегрирования
Таким образом общее решение неоднородного уравнения:

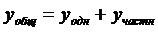
Пример:
1) 
РАЗДЕЛ: «Ряды»
Числовые ряды
Определение:Рассмотрим бесконечную числовую последовательность:
 числовым рядом называется выражение
числовым рядом называется выражение  , где
, где  – общий член ряда.
– общий член ряда.
Пример:
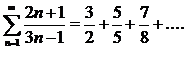 -знакоположительный ряд
-знакоположительный ряд
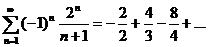 -знакочередующийся ряд
-знакочередующийся ряд
Последовательность  , где
, где  ;
; 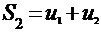 ;
; 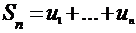 - последовательность частичных сумм ряда.
- последовательность частичных сумм ряда.
Каждая частичная сумма содержит конечное число слагаемых.
Числовой ряд 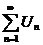 называется сходящимся, если существует конечный
называется сходящимся, если существует конечный
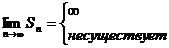 , то ряд называется расходящимся и суммы S не имеют.
, то ряд называется расходящимся и суммы S не имеют.
1)Рассмотрим ряд из членов геометрической прогрессии.
 , где n – частичная сумма ряда
, где n – частичная сумма ряда  - сумма n первых членов геометрической прогрессии.
- сумма n первых членов геометрической прогрессии.
Рассмотрим 3 случая:
1)  геометрическая прогрессия убывающая.
геометрическая прогрессия убывающая.
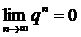
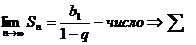 сходится и имеет сумму
сходится и имеет сумму 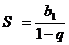
2) 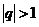

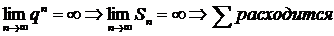
3) 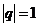
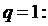
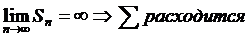

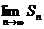 = не существует – ряд расходится.
= не существует – ряд расходится.
Вывод: ряд из членов геометрической прогрессии сходится если  и расходится
и расходится 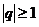

Элементарные свойства рядов
1) Если  (1) сходится и имеет сумму S, то
(1) сходится и имеет сумму S, то  (2) тоже сходится, и имеет сумму CS, где С-const.
(2) тоже сходится, и имеет сумму CS, где С-const.
Доказательство:Пусть  , n– ая частичная сумма 1 ряда.
, n– ая частичная сумма 1 ряда.
 , n–ая частичная сумма 2 ряда.
, n–ая частичная сумма 2 ряда.
Т.к 1 ряд сходится, то 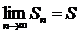 .
.
Рассмотрим 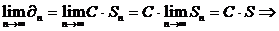 (2) ряд сходится.
(2) ряд сходится.
Конец доказательства.
2) Если 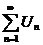 (1) сходится с суммой S1, и
(1) сходится с суммой S1, и 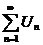 (2) сходится с суммой S2.
(2) сходится с суммой S2. 
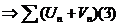 тоже сходится с суммой
тоже сходится с суммой 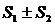 .
.
Доказательство:
Обозначим  - n – частичная сумма 1 ряда.
- n – частичная сумма 1 ряда.
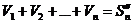 - n – частичная сумма 2 ряда.
- n – частичная сумма 2 ряда.
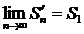

Рассмотрим n-ую частичную сумму ряда


 и сумма
и сумма  .
.
Конец доказательства.
3) Любой ряд может быть представлен в виде:
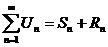 , где
, где  - n – частичная сумма
- n – частичная сумма
 - n – остаток ряда.
- n – остаток ряда.
n – остаток ряда  тоже является рядом.
тоже является рядом.
Если  , то и его остаток
, то и его остаток 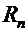 тоже сходится.
тоже сходится.
Доказательство: доказательство этого факта следует из того, что сумма ряда и сумма его остатка отличаются друг от друга на конечное число cлагаемых.
Конец доказательства.
Следствие: на сходимость ряда не влияет отбрасывание или приписывание в начало ряда конечного числа членов, например: 1+3+9+27+…
Дописывание : 1/9+1/3+1+3+9+27+.. отбрасывание: 1+3+5+7+9+11
4)Если 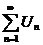 сходится с суммой S
сходится с суммой S 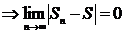 .
.
Общий вывод:на практике необязательно выяснять сходимость ряда по определению (вычисляя сумму S). Достаточно просто знать сходится этот ряд или расходится, поэтому, основное место в теории рядов занимают теоремы – признаки сходимости, которые позволяют исследовать ряд на сходимость, не вычисляя его суммы.
Признаки сходимости
Необходимый признак сходимости:
Если 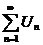 сходится, то общий член
сходится, то общий член 
Доказательство: Пусть  - n – частичная сумма.
- n – частичная сумма.
 - число.
- число.
При  ,
, 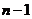 тоже
тоже 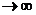 и
и  - n-1 – частичная сумма.
- n-1 – частичная сумма.
Она имеет предел  .
.
Т.к 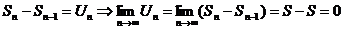
 конец доказательства.
конец доказательства.
Необходимый признак сходимости неудобен на практике, т.к по поведению общего члена Un на бесконечности нельзя судить о сходимости ряда.
На практике удобно пользоваться достаточным признаком расходимости ряда:
Если  не стремится к 0 при
не стремится к 0 при 

Примеры:
1) 
2) 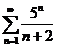
Радикальный признак Коши.
Дан ряд с положительными членами 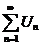 и
и 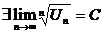
Если 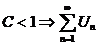 - сходиться
- сходиться
Если 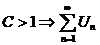 - расходиться
- расходиться
Если 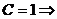 - вопрос о сходимости не решен
- вопрос о сходимости не решен
Доказательство:
по определению 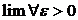
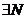 , начиная с которого
, начиная с которого 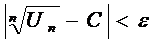
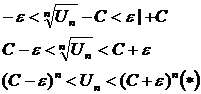
1) Пусть С<1 выберем 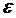 настолько малым, чтобы
настолько малым, чтобы 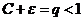 , тогда из правой части
, тогда из правой части 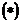

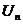 <
< 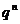 , ряд
, ряд 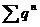 , где q<1 сходится как ряд из членов геометрической прогрессии, со знаменателем <1, тогда исходный ряд сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда.
, где q<1 сходится как ряд из членов геометрической прогрессии, со знаменателем <1, тогда исходный ряд сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда.
2) Пусть С>1 выберем 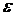 настолько малым, чтобы
настолько малым, чтобы 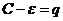 >1
>1  из левой части
из левой части 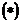
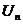 >
> 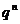 ;
; 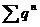 (q>1) расходится, как ряд из членов геометрической прогрессии, расходится по I признаку сравнения, т.к его члены больше членов сходящегося ряда.
(q>1) расходится, как ряд из членов геометрической прогрессии, расходится по I признаку сравнения, т.к его члены больше членов сходящегося ряда.
3)С=1
Возьмем 2 обобщенно гармонических ряда 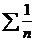 – расходится (p=1) и
– расходится (p=1) и 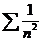 -сходится (p=2>1) и покажем, что С=1.
-сходится (p=2>1) и покажем, что С=1.
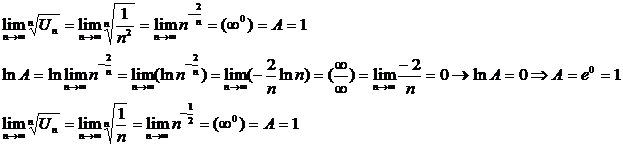
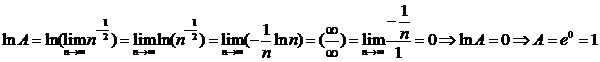
Таким образом при С=1 ряд может как сходится так и расходится.
Конец доказательства.
Примеры:
1) 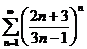
2) 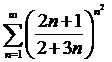
3) 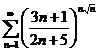
Интегральный признак Коши.
Дан ряд с положительными членами 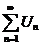 , что
, что 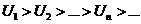 (
( 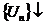 ) и функция f(x) – положительная и убывающая, связанная с рядом равенством f(n)=
) и функция f(x) – положительная и убывающая, связанная с рядом равенством f(n)= 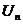 . Тогда несобственный интеграл
. Тогда несобственный интеграл 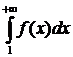 и
и 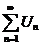 сходится и расходится одновременно.
сходится и расходится одновременно.
Доказательство:
f(n)=Un
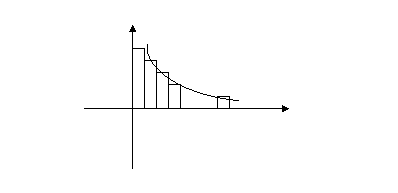
n
S ступенчатой фигуры над рядом (f(x))
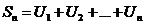 - n частичная сумма ряда.
- n частичная сумма ряда.
S ступенчатой фигуры под графиком функции f(x)
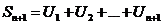 - n+1 частичная сумма ряда.
- n+1 частичная сумма ряда.
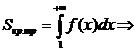 очевидно неравенство
очевидно неравенство 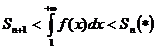
Пусть несобственный интеграл 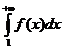 сходится
сходится 
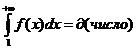
Из левой части 
 <числа
<числа 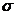

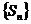 - ограничена сверху числом
- ограничена сверху числом 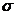

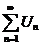 - сходится.
- сходится.
Пусть 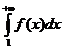 расходится
расходится 
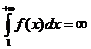
 из правой части (*)
из правой части (*) 
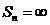

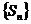 неограничен
неограничен  ряд расходится.
ряд расходится.
Конец доказательства.
Докажем, с помощью интегрального признака Коши, что обобщенно-гармонический ряд:
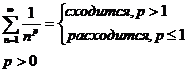
свяжем с эти рядом несобственный интеграл
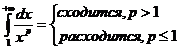 (доказано в несобственном интеграле)
(доказано в несобственном интеграле)  исходный несобственный интеграл сходится или расходится одновременно.
исходный несобственный интеграл сходится или расходится одновременно.
Примеры:
1) 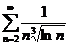
2) 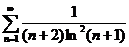
Функциональные ряды
Определение: 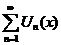 , где
, где 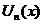 - функции переменной х называется функциональным рядом.
- функции переменной х называется функциональным рядом.
При некоторых значениях х функциональный ряд сходится, при других значениях х – расходится.
Определение:Множество значений переменной х, при которых функциональный ряд 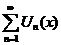 - сходится, называется областью сходимости функционального ряда. Задача нахождения области сходимости функционального ряда является весьма трудной, хотя для некоторых рядов область сходимости найти легко.
- сходится, называется областью сходимости функционального ряда. Задача нахождения области сходимости функционального ряда является весьма трудной, хотя для некоторых рядов область сходимости найти легко.
Пример:
1) 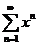
2) 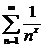
Степенные ряды
Определение:Степенным рядом называется ряд вида 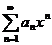 , где
, где 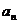 - коэффициент степенного ряда, зависит от n и не зависит от х.
- коэффициент степенного ряда, зависит от n и не зависит от х.
Степенной ряд является частным случаем функционального ряда, поэтому естественно поставить вопрос об области сходимости степенного ряда и его равномерной сходимости. Ответ на вопрос какой вид имеет область сходимости степенного ряда дает теорема Абеля.
Теорема Абеля:
Если 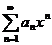 сходится в точке
сходится в точке 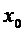
 он сходится во всех точках, удовлетворяющих неравенству
он сходится во всех точках, удовлетворяющих неравенству 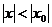 . Если
. Если 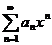 расходится в точке
расходится в точке 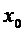
 он расходится во всех точках, удовлетворяющих неравенству
он расходится во всех точках, удовлетворяющих неравенству 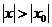 .
.
Доказательство:
Пусть 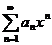 сходится в точке
сходится в точке 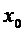
 будет сходится ряд
будет сходится ряд 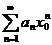
 по необходимому признаку сходимости
по необходимому признаку сходимости 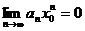
 числовая последовательность
числовая последовательность 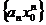 - ограничена, т.е существует число M>0, что
- ограничена, т.е существует число M>0, что 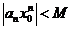 сразу для всех n.
сразу для всех n.
Возьмем любое х удовл. 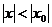 и рассмотрим
и рассмотрим 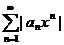 из абсолютных величин.
из абсолютных величин.
Оценим общий член этого ряда: 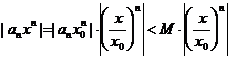
Ряд из членов геометрической прогрессии 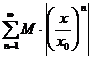 со знаменателем
со знаменателем 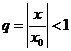 сходится
сходится  исходный
исходный 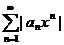 тоже сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда
тоже сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда 
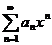 сходится абсолютно.
сходится абсолютно.
Пусть 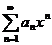 расходится в точке
расходится в точке 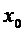 .
.
Возьмем любое х удовл. 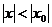 , нужно доказать, что
, нужно доказать, что 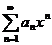 расходится при любом х, удовлетворяющем
расходится при любом х, удовлетворяющем 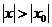 .
.
Предположим противное: 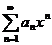 - сходится
- сходится  по 1 части доказательства он будет сходится в точке
по 1 части доказательства он будет сходится в точке 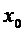 .
.
Полученное противоречие доказывает теорему.
Конец доказательства.
Из теоремы Абеля  что если степенной
что если степенной 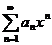 сходится в
сходится в 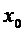
 он сходится в точке удовлетворяющей неравенству
он сходится в точке удовлетворяющей неравенству 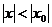 :
:
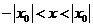
 сходится расходится
сходится расходится
расходится . .
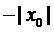 0
0 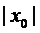
Если 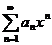 расходится в точке
расходится в точке 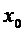 , тогда он расходится
, тогда он расходится 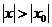
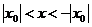
Вывод:существует интервал с центром в точке 0, радиусом R, внутри которого степенной ряд сходится, и вне которого расходится. Такой интервал называется интервалом сходимости степенного ряда, а R – радиусом сходимости степенного ряда. Укажем метод нахождения интервала сходимости.
Ряды Тейлора
На I курсе рассматривалась формула Тейлора для функции f(x) n+1 раз дифференцируемая в окрестности точки 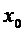 .
.
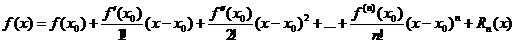
где 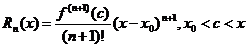
 Если f(x) любое число раз дифференцируема в окрестности точки
Если f(x) любое число раз дифференцируема в окрестности точки 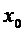

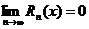 переходя к пределу
переходя к пределу  в формуле Тейлора получим:
в формуле Тейлора получим:
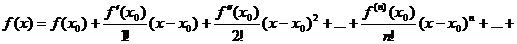
ряд стоящий в правой части равенства называется рядом Тейлора для функции f(x) по степеням 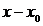 , а сама формула называется разложением функции f(x) в ряд Тейлора.
, а сама формула называется разложением функции f(x) в ряд Тейлора.
 Формально ряд Тейлора может быть получен для любой функции, но сходится к этой функции он будет только тогда, когда
Формально ряд Тейлора может быть получен для любой функции, но сходится к этой функции он будет только тогда, когда 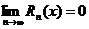
Если этот предел 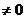 , то ряд либо расходится, либо сходится к совсем другой функции.
, то ряд либо расходится, либо сходится к совсем другой функции.
Ряды Маклорена
Если в ряде Тейлора 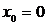 , то получим ряд Маклорена по степеням х.
, то получим ряд Маклорена по степеням х.
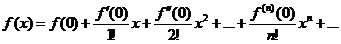
Остаточный член 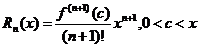
Получим разложение некоторых элементарных функций в ряд Маклорена и найдём интервалы сходимости этих рядов.
 1)
1) 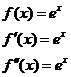
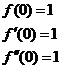
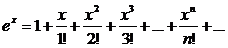 Интервал сходимости этого ряда найдем непосредственно по признаку Даламбера.
Интервал сходимости этого ряда найдем непосредственно по признаку Даламбера.
Интервал сходимости 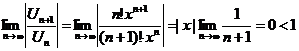
 При любом х ряд сходится по признаку Даламбера.
При любом х ряд сходится по признаку Даламбера.
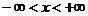 - интервал сходимости.
- интервал сходимости.
2)
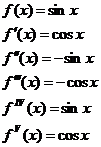
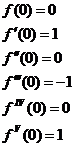

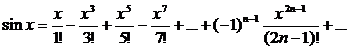
 т.к семейство производных любого порядка равномерно ограничено
т.к семейство производных любого порядка равномерно ограничено  при
при 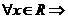 интервал сходимости
интервал сходимости 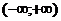
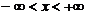
3)
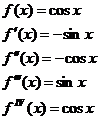
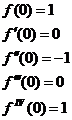


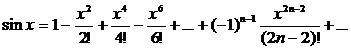
 - интервал сходимости.
- интервал сходимости.
4) Биномиальное разложение

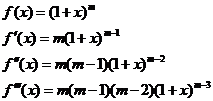
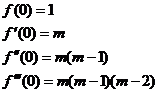

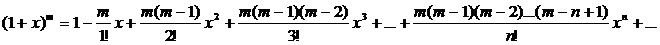
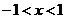 - интервал сходимости.
- интервал сходимости.
5) f(x)=ln(1+x)
Воспользуемся предыдущим биномиальным разложением:
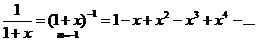
проинтегрируем почленно на отрезке 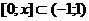
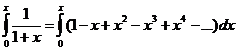
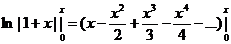
 снимем модуль, т.к 1+х>0
снимем модуль, т.к 1+х>0

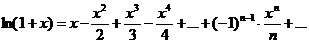
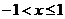 - можно показать.
- можно показать.
6) f(x)=arctgx
воспользуемся биномиальным разложением и заменим 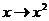
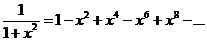
проинтегрируем на 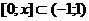
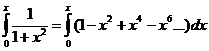


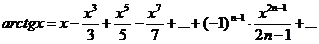
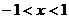
Введение
При изучении некоторых явлений часто возникает ситуация, когда процесс не удаётся описать с помощью уравнения y=f(x) или F(x;y)=0. Помимо переменной х и неизвестной функции , в уравнение входит производная этой функции.
Определение:Уравнение, связывающее переменную х, неизвестную функцию y(x) и её производные называется дифференциальным уравнением. В общем виде дифференциальное уравнение выглядит так:
F(x;y(x);  ;
; 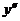 ;...;y(n))=0
;...;y(n))=0
Определение:Порядком дифференциального уравнения называется порядок входящей в него старшей производной.
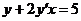 – дифференциальное уравнение 1 порядка
– дифференциальное уравнение 1 порядка
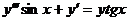 – дифференциальное уравнение 3 порядка
– дифференциальное уравнение 3 порядка
Определение:Решением дифференциального уравнения является функция, которая при подстановке в уравнение обращает его в тождество.
Дифференциальные уравнения 1 порядка
Определение: Уравнение вида 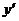 =f(x;y) или F(x;y;
=f(x;y) или F(x;y; 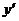 )=0 называется дифференциальным уравнением 1 порядка.
)=0 называется дифференциальным уравнением 1 порядка.
Определение:Общим решением дифференциального уравнения 1 порядка называется функция y=γ(x;c), где (с –const), которая при подстановке в уравнение обращает его в тождество. Геометрически на плоскости общим решением соответствует семейство интегральных кривых, зависящих от параметра с.
|
Примеры: