Данные для расчета автокорреляции

t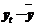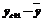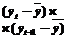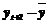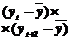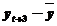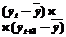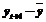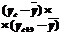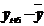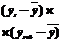
	40,2	11,2	450,24	22,2	892,44	-30,8	-1238,16	-16,8	-675,36	25,2	-423,36
	11,2	22,2	248,64	-30,8	-344,96	-16,8	-188,16	25,2	282,24	37,2	937,44
	22,2	-30,8	-683,76	-16,8	-372,96	25,2	559,44	37,2	825,84	1,2	44,64
	-30,8	-16,8	517,44	25,2	-776,16	37,2	-1145,76	1,2	-36,96	-62,8	-75,36
	-16,8	25,2	-423,36	37,2	-624,96	1,2	20,16	-62,8	1055,04	-26,8	-1683,04
	25,2	37,2	937,44	1,2	30,24	-62,8	-1582,56	-26,8	-675,36
	37,2	1,2	44,64	-62,8	-2336,16	-26,8	-996,96
	1,2	-62,8	-75,36	-26,8	-32,16
	-62,8	-26,8	1683,04
	-26,8
Σ			2698,96		-3564,68		-4572		775,44		-1196,68

Определяем среднее значение дисперсии δ²:

δ²=1/10(40,2²+11,2²+22,2²+(-30,8)²+(-16,8)²+25,2²+…+(-26,8)²)=1014,76.

Вычисляем коэффициенты автокорреляции:

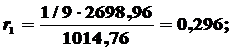
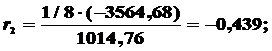
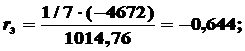
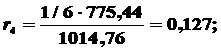
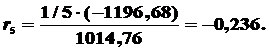
Представим полученные значения на графике. Откуда видно,

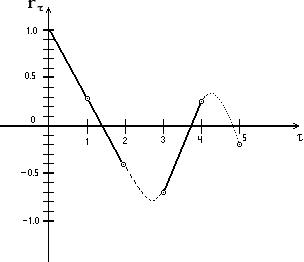
Рис. 7.2. График автокорреляции ВР

что коэффициент автокорреляции имеет колебательный затухающий характер. Это говорит о том, что по мере удаления от данной точки t стохастическая связь между значениями членов ВР уменьшается.

Формирование набора моделей прогнозирования

Методология экономического прогнозирования

Основная цель создания трендовых моделей экономической динамики – это сделать на их основе прогноз о развитии изучаемого процесса на предстоящий промежуток времени.

После того, как предварительный анализ информации убедил нас в том, что данные сопоставимы, однородны, аномальных наблюдений нет, число наблюдений достаточно для проявления тенденций, исследуемый процесс устойчив, а тенденция прослеживается отчётливо, можно приступить к подбору трендовых моделей и разработке прогноза.

Экономическое прогнозирование базируется на идее, что закономерность развития экономического процесса, действовавшая в прошлом (внутри ВР), сохранится и в прогнозируемом будущем, т.е. прогноз основан на экстраполяции (нахождение по ряду данных значений функции других её значений, находящихся вне этого ряда). Экстраполяция, проводимая в будущее, называется перспективной, а в прошлое – ретроспективной.

Прогнозирование методом экстраполяциибазируется на следующих предпосылках:

а) развитие исследуемого явления в целом следует описывать плавной кривой;

б) общая тенденция развития явлений в прошлом и в настоящем не должна претерпевать серьёзных изменений в будущем;

в) учет случайности позволяет оценить вероятность отклонения от закономерного развития.

Наиболее распространён метод экстраполяции на основе кривых роста экономической динамики.

Кривые роста и их выбор

Плавную кривую (гладкую функцию), аппроксимирующую ВР, принято называть кривой роста. Использование метода экстраполяции на основе кривых роста для прогнозирования базируется на двух предположениях:

- ВР экономического показателя действительно имеет тренд;

- общие условия, определяющие развитие показателя в прошлом, останутся без существенных изменений в течении периода упреждения.

Известно большое количество типов кривых роста для экономических процессов.