Дифференциал сложной функции

Функция многих переменных

Пусть x, y, z,...,t - независимые переменные, а u - величина, зависимая от них.

Величина u называется функцией переменных величин x, y, z,...,t, если каждой рассматриваемой совокупности этих величин соответствует одно определенное значение величины u и пишут: u=f(x,y,z,...,t).

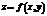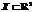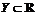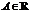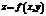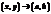Пусть дана функция с областью определения и множеством значений . Говорят, что точка является пределом функции при и пишут 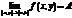или 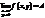, если .

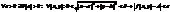Повторный предел

предел функции нескольких переменных, при к-ром предельный переход совершают последовательно по различным переменным. Пусть, напр., функция f двух переменных х и у определена на множестве вида 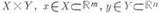, и пусть х 0, y0 - предельные точки соответственно множеств X и Y или символы оо (в случае, когда m=1 или n=1, х 0 и соответственно y0 могут быть бесконечностями со знаком: ). Если при любом фиксированном 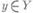существует предел

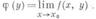
(1) и у функции j(у).существует предел

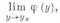
то этот предел наз. повторным пределом

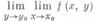(2)

функции f(x, у).в точке ( х 0, у 0)

Частная производная ФМП

В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

В явном виде частная производная функции f определяется следующим образом:

Дифференциал ФМП

Функция Z=f(x,y) называется дифференцируемой в точке P(x,y), если ее полное приращение ΔZ можно представить в виде Δz = A∙Δx+B∙Δy+ω(Δx,Δy), где Δx и Δy – любые приращения соответствующих аргументов x и y в некоторой окрестности точки Р, А и В – постоянные (не зависят от Δx,Δy),

ω(Δx,Δy) – бесконечно малое более высокого порядка, чем расстояние: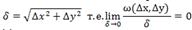

Если функция Z=f(x,y) дифференцируема в точке P(x,y), то она имеет в точке Р первые частные производные:

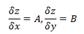
Теорема 2:

Если же частные производные непрерывны в окрестности точки Р, то эта функция дифференцируема, т.е существует дифференциал.

Дифференциал сложной функции

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x0, а функция g имеет производную в точке y0 = f(x0), то сложная функция h(x) = g(f(x)) также имеет производную в точке x0.

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

Теорема о равенстве смешанных производных

Если в некоторой окрестности точки 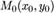функция 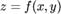имеет смешанные частные производные 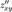и 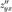, причём эти смешанные частные производные непрерывны в точке м0 , то они равны в этой точке: .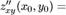

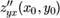Геометрический смысл дифференциала функции двух переменных

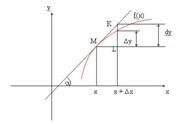
Из треугольника DMKL: KL = dy = tga×Dx = y¢×Dx

Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.

Частные производные высших порядков

Формула Тейлора

Пусть функция f(x,y) имеет полные производные вплоть до n-го порядка включительно в некоторой окрестности точки (x0,y0). Введём дифференциальный оператор

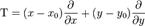
Тогда разложением в ряд Тейлора функции f(x,y) по степеням (x − x0)k и (y − y0)k в окрестности точки (x0,y0) будет

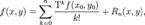
где Rn(x,y) — остаточный член в форме Лагранжа:

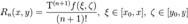
В случае функции одной переменной 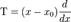, поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе T.

Неявная ФМП

при выполнении соответствующих условий, уравнение 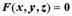задает неявно функцию 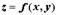. Это же уравнение может задавать неявно функцию 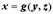или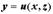

Экстремум ФМП

Пусть функция f (х, у) определена в точке M0 (x0, y0) и в некоторой её окрестности. Функция f (х, у) имеет максимум в точке(x0, y0), если f (x0, y0) > f (х, у) для всех точек (х, у). из некоторой окрестности точки(x0, y0). Если же f (x0, y0) < f (х, у)., то функция f (х, у) имеет минимум в точке M0 (x0, y0). Точки, в которых функция принимает максимальное и минимальное значения, называются экстремальными.

Метод наименьших квадратов

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Двойной интеграл

Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как

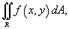
где R - область интегрирования в плоскости Oxy. Если определенный интеграл 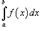от функции одной переменной 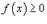выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости Oxy в области интегрирования R

Повторный интеграл

понятие интегрального исчисления. Вычисление двойного интеграла

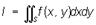
от функции f (x, у) по области S, ограниченной прямыми х = а, х = b и кривыми y = φ1(x), у = φ2(х), при некоторых условиях относительно функций f (x, у), φ1(x), φ2(х), производится по формуле:

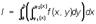
где при вычислении внутреннего интеграла х считается постоянным.

Тройной интеграл

Тройным интегралом называют кратный интеграл с d=3.

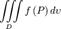
Здесь 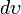— элемент объема в рассматриваемых координатах.

В прямоугольных координатах 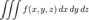, где 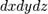является элементом объема в прямоугольных координатах.

Якобиан

функциональный определитель ½aik½1n с элементами 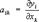, где yi = fi (X1,..., Xn), l £ i £ n, — функции, имеющие непрерывные частные производные в некоторой области А; обозначение:

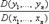
Якобиан часто применяется при анализе неявных функций

Равенство определителя Якоби нулю служит удобным необходимым и достаточным условием вырожденности преобразования координат, а неравенство его нулю — необходимым и достаточным условием невырожденности.

Замена переменных

Для вычисления двойного интеграла иногда удобнее перейти в другую систему координат.

Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции.

В новой системе координат вычисление двойного интеграла значительно упрощается.

Замена переменных в двойном интеграле описывается формулой

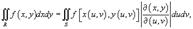
где 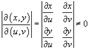выражение представляет собой так называемый якобиан преобразования 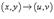, а S − образ области интегрирования R, который можно найти с помощью подстановки 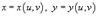в определение области R. Отметим, что в приведенной выше формуле 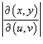означает абсолютное значение соответствующего определителя.

Двойной интеграл

Пусть область D ограничена линией r = r( ) и лучами = и = , где и r – полярные координаты точки на плоскости, связанные с ее декартовыми координатами x и y

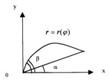
Рис. 5

соотношениями 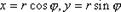(рис. 5). В этом случае

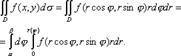
Замечание. Если область D в декартовых координатах задается уравнением, содержащим бином , например, и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах.

Если область D в декартовых координатах задается уравнением, содержащим бином 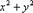, например, 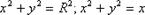и т.д., то вычисление двойного интеграла по такой области удобнее производить в полярных координатах.

Кратные интегралы

Кратный интеграл, интеграл от функции, заданной в какой-либо области на плоскости, в трёхмерном или n-мерном пространстве. Среди К. и. различают двойные интегралы, тройные интегралы и т. д. n-кратные интегралы.

Пусть функция f (x, y) задана в некоторой области D плоскости хОу. Разобьем область D на n частичных областей di, площади которых равны si, выберем в каждой области di точку (xi, hi) (см. рис.) и составим интегральную сумму

.

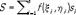
Нормаль к поверхности

Одной из основных характеристик поверхности является её нормаль — единичный вектор, перпендикулярный касательной плоскости в заданной точке:

.

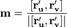
Знак нормали зависит от выбора координат.

Функция многих переменных

Пусть x, y, z,...,t - независимые переменные, а u - величина, зависимая от них.

Величина u называется функцией переменных величин x, y, z,...,t, если каждой рассматриваемой совокупности этих величин соответствует одно определенное значение величины u и пишут: u=f(x,y,z,...,t).

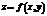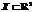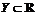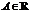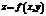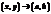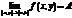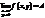Пусть дана функция с областью определения и множеством значений . Говорят, что точка является пределом функции при и пишут или , если .

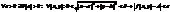Повторный предел

предел функции нескольких переменных, при к-ром предельный переход совершают последовательно по различным переменным. Пусть, напр., функция f двух переменных х и у определена на множестве вида 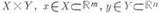, и пусть х 0, y0 - предельные точки соответственно множеств X и Y или символы оо (в случае, когда m=1 или n=1, х 0 и соответственно y0 могут быть бесконечностями со знаком: ). Если при любом фиксированном 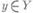существует предел

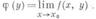
(1) и у функции j(у).существует предел

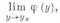
то этот предел наз. повторным пределом

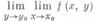(2)

функции f(x, у).в точке ( х 0, у 0)

Частная производная ФМП

В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

В явном виде частная производная функции f определяется следующим образом:

Дифференциал ФМП

Функция Z=f(x,y) называется дифференцируемой в точке P(x,y), если ее полное приращение ΔZ можно представить в виде Δz = A∙Δx+B∙Δy+ω(Δx,Δy), где Δx и Δy – любые приращения соответствующих аргументов x и y в некоторой окрестности точки Р, А и В – постоянные (не зависят от Δx,Δy),

ω(Δx,Δy) – бесконечно малое более высокого порядка, чем расстояние: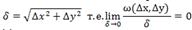

Если функция Z=f(x,y) дифференцируема в точке P(x,y), то она имеет в точке Р первые частные производные:

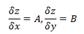
Теорема 2:

Если же частные производные непрерывны в окрестности точки Р, то эта функция дифференцируема, т.е существует дифференциал.

Дифференциал сложной функции

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x0, а функция g имеет производную в точке y0 = f(x0), то сложная функция h(x) = g(f(x)) также имеет производную в точке x0.

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.