Свойство математического ожидания.
Теорема 1. Математическое ожидание постоянной величины равно самой постоянной.
То есть, если C - постоянная величина, то
M(C)=C
Теорема 2. Математическое ожидание суммы двух (или нескольких) случайных величин равно сумме математических ожиданий слагаемых. То есть если X и Y - случайные величины, то.
M(X+Y)=M(x)+M(Y).
Следствие. Если С - постоянная величина, то M(X + С) = M (X) + С .
Теорема 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
m(xy)=m{x)0*m{y).
Следствие 1. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
Следствие 2. Постоянный множитель можно выносить за знак математического ожидания:
M(CX)=CM(X)
Следствие 3 Математическое ожидание разности любых двух случайных величин X и Y равно разности математических ожиданий этих величин
M(X-Y)=M(X)-X(Y)
Отклонение случайной величины.
Отклонением называют разность между случайной величиной и её математическим ожиданием
Теорема. Для любой случайной величины математическое ожидание её отклонения равно нулю, то есть M[X-M(X)]=0
X – случайная величина
M(X ) -её математическое ожидание
Дисперсия дискретной случайной величины.
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания.
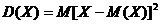
Дисперсия непрерывной случайной величины.
Это математическое ожидание квадрата отклонения этой случайной величины от её среднего значения
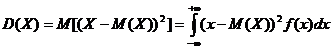,где f(x) – плотность вероятности случайной величины X
Теорема: Дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины (X)и квадратом математического ожидания, то есть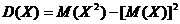 
Свойства дисперсии.
Теорема 1: Дисперсия постоянной величины равна нулю, то есть D(C)=0
Теорема 2: Дисперсия суммы двух независимых случайных величин X и Y равна сумме дисперсий этих величин: D(X+Y)=D(X)+D(Y)
Следствие 1. Дисперсия сумм нескольких взаимно независимых величин равна сумме дисперсий этих величин.
Следствие 2. Если C - постоянная величина, то D(X+C)=D(X)
Следствие 3. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин, то есть если случайные величины и независимы, то
D(X-Y)=D(X)+D(Y)
Теорема 3: Постоянный множитель можно выносить за знак дисперсии возводя его в квадрат: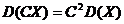 
Среднее квадратичное отклонение.
Это квадратный корень из дисперсии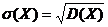 
Начальный момент порядка К.
Это математическое ожидание величины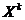 
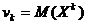
Связь между начальными и центральными порядками.
Центральный момент порядка К.
Это математическое ожидание величины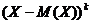 
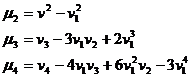
Нормальное распределение.
Это распределение вероятностей непрерывной случайной величины, которая описывается плотностью
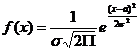определяется двумя параметрами
a – математическое ожидание
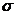- среднее квадратическое отклонение нормального распределения
Если a=0 и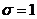 
, то нормальное распределение называют нормированием
Формула Бейеса.
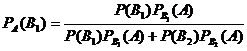
Статистическая вероятность.
Наряду с классическим определением вероятности используются и другие определения, в частности, статистическое определение: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.
Пример. Если в результате достаточно большого числа испытаний оказалось, что относительная частота близка к числу 0,4, следовательно, это число можно принять за статистическую вероятность события.
Недостатком статистического определения вероятности является неоднозначность: так, в приведённом примере в качестве вероятности события можно принять не только 0,4, но и 0,39; 0,41 и т. Д
Асимметрия и эксцесс
Асимметрией теоретического распределения, то есть распределения вероятностей, называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
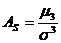
Асимметрия положительна, если «длинная часть» кривой расположена слева от математического ожидания и отрицательна, если расположена справа.
Эксцесс определяется равенством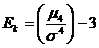 
Для нормального распределения 