Решение систем линейных уравнениЙ

Тема 1. Определители.

Решение систем линейных уравнениЙ

Вопросы для самопроверки

1. Перечислите свойства определителей.

2. Какие способы вычисления определителей вы знаете?

3. Сформулируйте правило Крамера.

4. Сформулируйте условие, при котором система линейных уравнений имеет единственное решение, не имеет решений, имеет бесчисленное множество решений.

Рекомендации к решению задания

Пусть требуется, используя формулы Крамера, решить систему:

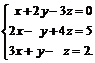
Подсчитаем сначала главный определитель системы 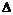, воспользовавшись следующим правилом вычисления определителей третьего порядка.

.

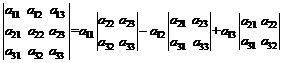В нашем случае

.

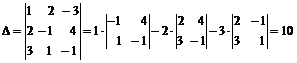Так как D¹0, делаем вывод о том, что система имеет единственное решение. Для его отыскивания вычислим вспомогательные определители D_x, D_y, D_z:

,

,

.

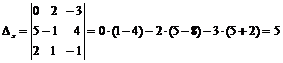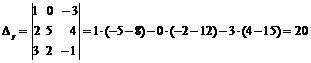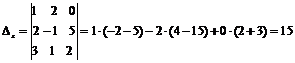Далее, воспользовавшись формулами Крамера, получим:

, , .

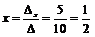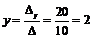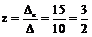Задание 1

Задачи 1–20.Решить заданную систему уравнений, пользуясь формулами Крамера.

1.		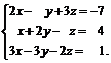2.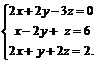
3.		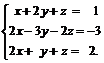4.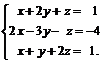
5.		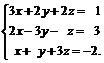6.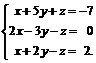
7.		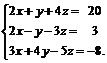8.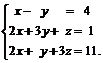
9.		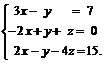10.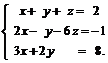
11.		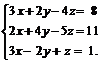12.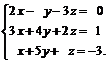
13.		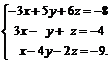14.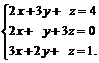
15.		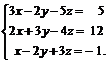16.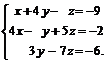
17.		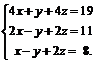18.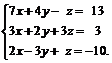
19.		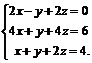20.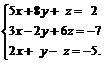

Тема 2. Элементы

Аналитической геометрии на плоскости

Вопросы для самопроверки

1. Напишите формулу для вычисления расстояния между двумя точками на плоскости.

2. Напишите уравнение прямой с угловым коэффициентом. В чем состоит геометрический смысл углового коэффициента?

3. Запишите уравнение прямой, проходящей через две точки на плоскости.

4. Как найти угловой коэффициент прямой, если дано ее общее уравнение?

5. Как вычислить угол между прямыми, заданными уравнениями с угловыми коэффициентами ?

6. Как найти координаты точек пересечения двух прямых, если даны их уравнения?

Рекомендации к решению задания

Пусть даны координаты вершин DABC: A(1; 3); B(10; 9); C(15; 1). Требуется найти : 1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) тангенс угла В; 4) уравнение высоты CD; 5) уравнение медианы AE; 6) уравнение прямой, проходящей через точку С параллельно стороне AB; 7) сделать чертеж.

1. Расстояние между точками A(x₁; y₁) и B(x₂; y₂) определяется по формуле

,

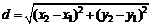поэтому .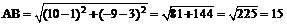

2. Уравнение прямой, проходящей через точки A(x₁, y₁) и B(x₂, y₂), имеет вид

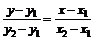. (1)

Подставив в уравнение (1) координаты точек A и B, получим уравнение стороны AB:

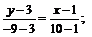
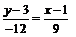; 3y–9= –4x+4; –4x–3y+13=0 (AB).

Решив последнее уравнение относительно y, получим

.

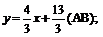
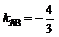Подставив в уравнение (1) координаты точек В и С, получим уравнение прямой ВС:

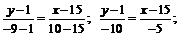y–1=2(x–15); 2x–y–29=0(BC); y=2x–29; k_BC=2.

3. Известно, что тангенс угла j между двумя прямыми вычисляется по формуле

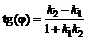. (2)

Искомый угол B образован прямыми AB и BC. Угловые коэффициенты этих прямых соответственно равны 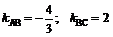, поэтому тангенс угла В будет вычисляться следующим образом:

.

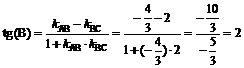4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид

y–y₁=k(x–x₁). (3)

Высота CD перпендикулярна стороне AB. Чтобы найти угловой коэффициент высоты CD, воспользуемся условием перпендикулярности прямых. Так как 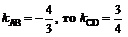. Подставив в уравнение (3) координаты точки C и угловой коэффициент высоты CD, получим:

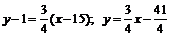(CD).

5. Чтобы найти уравнение медианы AE, определим сначала координаты точки E, которая является серединой стороны BC, применяя формулы деления отрезка пополам:

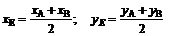, (4)

.

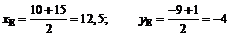Подставив в уравнение (1) координаты точек A и E, находим уравнение медианы:

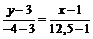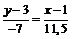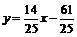; ; (AE).

6. Так как искомая прямая параллельна стороне AB, то ее угловой коэффициент будет равен угловому коэффициенту прямой AB. Подставив в уравнение (3) координаты точки C и угловой коэффициент 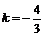, получим 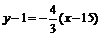, 4x+3y–63=0 (KF).

7. Сделаем чертеж (рис. 1).

Задание 2

Задачи 21–40. Даны координаты вершин DABC. Требуется найти: 1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) тангенс угла В; 4) уравнение высоты CD; 5) уравнение медианы AE; 6) уравнение прямой, проходящей через точку С параллельно стороне AB; 7) сделать чертеж.

Номер задачи	A	B	C
	(–2; –3)	(0; 7)	(8; 3)
	(5; 4)	(7; 14)	(15; 10)
	(–1; 5)	(1; 15)	(9; 11)
	(0; 3)	(2; 13)	(10; 9)
	(3; 0)	(5; 10)	(13; 6)
	(2; –5)	(4; 5)	(12; 1)
	(–3; –2)	(–1; 8)	(7; 4)
	(4; 1)	(6; 11)	(14; 7)
	(–4; –1)	(–2; 9)	(6; 5)
	(1; 2)	(3; 12)	(11; 8)
	(–8; –3)	(4; –12)	(8; 10)
	(–7; 6)	(2; –6)	(7; 4)
	(–5; 7)	(4; –5)	(9; 5)
	(–3; 5)	(6; –7)	(11; 3)
	(–6; 10)	(3; –2)	(8; 8)
	(–4; 10)	(5; –4)	(10; 6)
	(–8; 9)	(1; –3)	(7; 7)
	(–9; 12)	(0; 0)	(5; 10)
	(–2; 11)	(7; –1)	(12; 9)
	(–1; 4)	(8; –8)	(13; 2)

Тема 3. ВЕКТОРЫ.

УРАВНЕНИЯ ПРЯМОЙ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ

Вопросы для самопроверки

1. Что называется вектором? Запишите его координаты.

2. Какие линейные операции можно выполнять с векторами?

3. Что называется скалярным произведением двух векторов?

4. Дайте определение векторного произведения двух векторов. Запишите формулу вычисления векторного произведения двух векторов, заданных координатами.

5. Напишите уравнение плоскости, проходящей через точку перпендикулярно заданному вектору.

6. Напишите каноническое уравнение прямой в пространстве.

7. Как найти объем пирамиды, построенной на трех некомпланарных векторах?

Рекомендации к решению задания

Пусть даны координаты вершин пирамиды АВСD: А(8; 6; 7); В(–2; 2; –1); С(–3; 4;–3) D(5; 8; 5). Требуется:

1) записать векторы 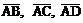в системе орт 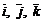и найти модули этих векторов;

2) найти косинус угла между векторами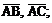

3) найти проекцию вектора 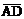на вектор ;

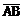4) найти площадь грани АВС;

5) найти объем пирамиды АВСD;

6) составить уравнение грани АВС.

Произвольный вектор представляется в системе орт 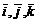формулой

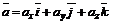, (1)

где а_х, а_у, а_z – координаты вектора .

Если заданы точки М(х₁; у₁; z₁) и N(х₂; у₂; z₂), то координаты вектора 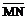соответственно равны а_х= х₂ – х₁; а_у=у₂–у₁; а_z=z₂–z₁ и вектор имеет вид

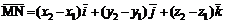. (2)

1. Применим формулу (2) для векторов 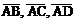, получим векторы: ; ; .

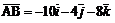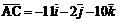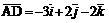Если вектор задан координатами, то модуль этого вектора вычисляется по формуле

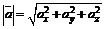. (3)

Применяя выражение (3), получим:

;

;

.

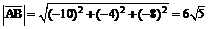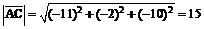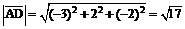2. Из формулы скалярного произведения вектора на вектор 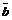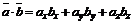имеем:

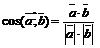. (4)

Применяя формулу (4) для векторов 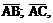получим:

.

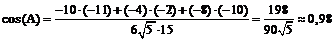Проекция вектора на вектор 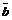есть 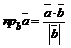, тогда

.

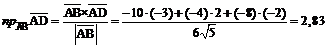4. Площадь грани АВС будем вычислять по формуле 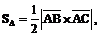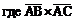– векторное произведение векторов.

Найдем векторное произведение векторов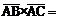

.

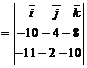
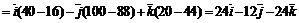Определим модуль векторного произведения:

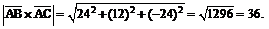
Тогда .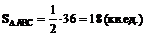

5. Объем пирамиды АВСD определим по формуле

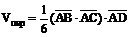. (5)

Найдем смешанное произведение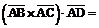

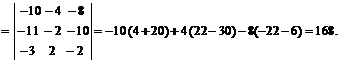
Тогда .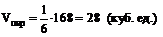

6. Чтобы получить уравнение грани АВС, нужно составить уравнение плоскости, проходящей через точки А, В, С. Это уравнение имеет вид

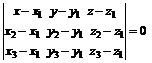. (6)

Тогда ; ;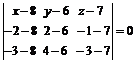

.

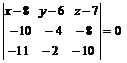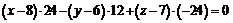Разделим на 12 обе части уравнения, в результате уравнение грани будет иметь вид .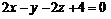

Задание 3

Задачи 41–60. Даны координаты вершин пирамиды АВСD. Требуется:

1) записать векторы 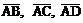в системе орт 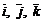и найти модули этих векторов;

2) найти косинус угла между векторами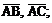

3) найти проекцию вектора 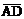на вектор ;

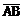4) найти площадь грани АВС;

5) найти объем пирамиды АВСD;

6) составить уравнение грани АВС.

Номер задач	А	В	С	D
	(2; 1; 0)	(3; –1; 2)	(13; 3; 10)	(0; 1; 4)
	(0; –2; –1)	(2; 4; –2)	(3; 2; 0)	(–11; 8; 10)
	(5; –1; –4)	(9; 3; –6)	(7; 10;–14)	(5; 1; –3)
	(1; –4; 0)	(5; 0; –2)	(3; 7; –10)	(1; –2; 1)
	(–3; –6; 2)	(1; –2; 0)	(–1; 5; –8)	(–3; –4; 3)
	(4; 8; 1)	(0; 4; 3)	(2; 15; –7)	(0; 6; 4)
Номер задач	А	В	С	D
	(2; 4; –4)	(0; 11; –12)	(–2; 0; –2)	(–2; 2; –1)
	(3; 3; –3)	(7; 7; –5)	(3; 5; –2)	(5; 14; –13)
	(6; 9; –5)	(8; 2; 3)	(4; –2; 5)	(4; 0; 6)
	(–4; –2; 3)	(6; 2; 11)	(–5; 0; 1)	(3; 4; 9)
	(2; –6; 2)	(12; –2; 10)	(1; –4; 0)	(9; 0; 8)
	(–2; –2; –8)	(0; –4; –6)	(10; 0; 2)	(7; 2; 0)
	(1; 0; –8)	(11; 4; 0)	(0; 2; –10)	(8; 6; –2)
	(4; –1; 0)	(3; 1; –2)	(14; 3; 8)	(11; 5; 6)
	(2; –3; 1)	(6; 1; –1)	(4; 8; –9)	(2; –1; 2)
	(9; 3; –6)	(7; 10; –14)	(5; –1; –4)	(5; 1; –3)
	(–1; –5; 4)	(9; –1; 12)	(–2; –3; 2)	(6; 1; 10)
	(–4; 5; –5)	(7; 7; 5)	(–3; 3; –3)	(4; 9; 3)
	(3; –3; –2)	(13; 1; 6)	(2; –1; –4)	(10; 3; 4)
	(–7; 1; 1)	(–8; 3; –1)	(3; 5; 9)	(0; 7; 7)

Вопросы для самопроверки

1. Какая величина называется постоянной, переменной?

2. Что называется функцией, областью определения функции?

3. Какая величина называется бесконечно малой, бесконечно большой?

4. Что называется пределом функции?

5. Сформулируйте теоремы о пределах.

6. Дайте определение непрерывности функции в точке, в интервале и на отрезке.

7. Что называется точкой разрыва?

Рекомендации к решению задания

;

.

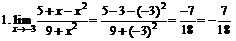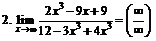При подстановке в функцию предельного значения аргумента получилась неопределенность вида 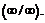Чтобы ее раскрыть, разделим числитель и знаменатель дроби на икс в наивысшей степени, т. е. х³.

.

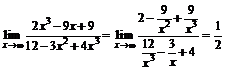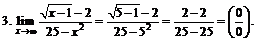
При подстановке в функцию предельного значения аргумента получилась неопределенность вида 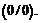Умножим числитель и знаменатель дроби на выражение, сопряженное числителю:

.

.

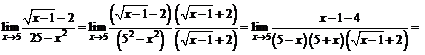
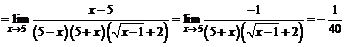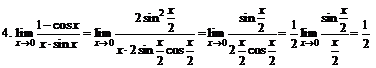Задание 4

Задачи 61–80.Найти пределы функций.

61.		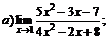	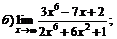в) ;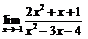
	.
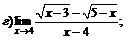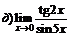62.		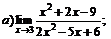	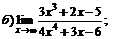в)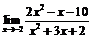
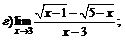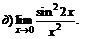63.		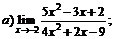	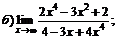в)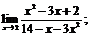
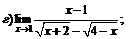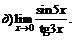64.		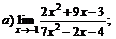	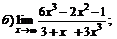в)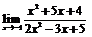
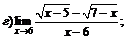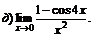65.		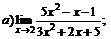	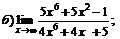в)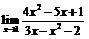
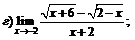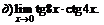66.		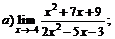	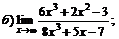в)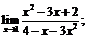
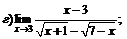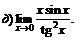67.		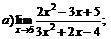	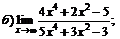в)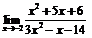
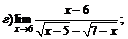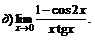68.		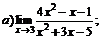	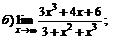в)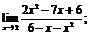
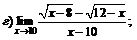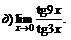69.		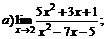	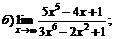в)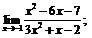
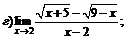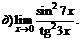70.		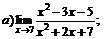	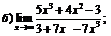в)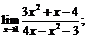
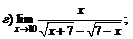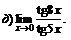71.		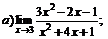	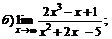в)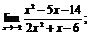
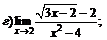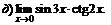72.		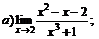	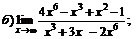в)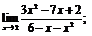
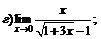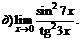73.		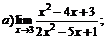	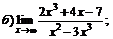в)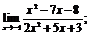
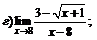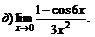74.		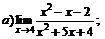	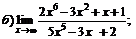в) ;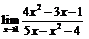
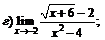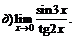75.		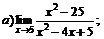	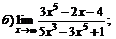в)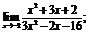
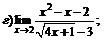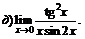76.		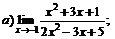	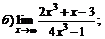в)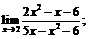
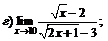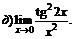77.		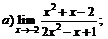	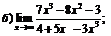в)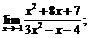
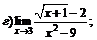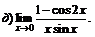78.		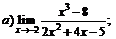	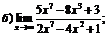в)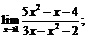
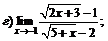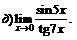79.		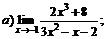	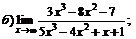в)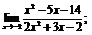
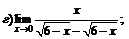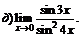80.		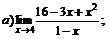	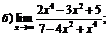в) ;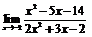

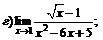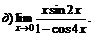Тема 5. Производная функции. Ее применение.

Геометрический и физический смысл

Вопросы для самопроверки

1. Объясните понятие средней скорости изменения функции, мгновенной скорости изменения функции.

2. Дайте определение производной функции.

3. Сформулируйте геометрический смысл производной функции в точке.

4. Чему равна производная от постоянной величины, от аргумента?

5. Чему равны производные от основных элементарных функций?

6. Сформулируйте правила дифференцирования суммы, произведения и частного двух функций.

7. Сформулируйте правило дифференцирования сложной функции.

8. Дайте определение дифференциала функции в точке.

9. Напишите формулу для вычисления дифференциала функции в точке.

10. В чем суть правила Лопиталя при раскрытии неопределенностей?

Рекомендации к решению заданий

Для решения заданий 5 – 7 необходимо знать правила дифференцирования и таблицу производных основных элементарных функций.

Правила дифференцирования:

1. 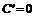;	2. ;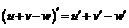
3. 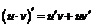;	4. .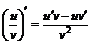

Производные основных элементарных функций:

1.	;	.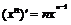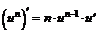
2.	;	.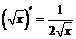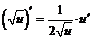
3.	;	.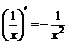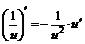
4.	;	.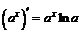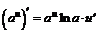
5.	;	.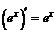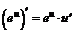
6.	;	.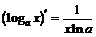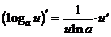
7.	;	.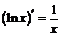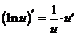
8.	;	.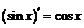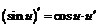
9.	;	.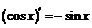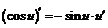
10.	;	.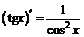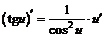
11.	;	.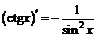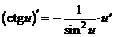
12.	;	.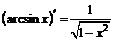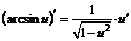
13.	;	.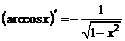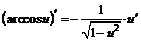
14.	;	.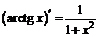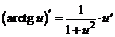
15.	;	.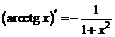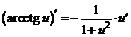

В левом столбце приведенной выше таблицы записаны производные основных элементарных функций, в правом – производные соответствующих сложных функций.

Найдем производные заданных функций.

1. .

+ .

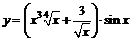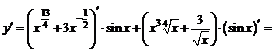
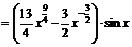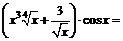
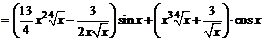2. .

.

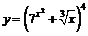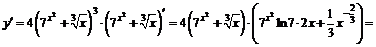
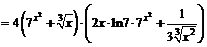3. .

.

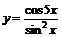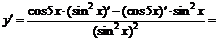
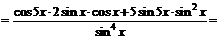
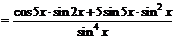4. .

.

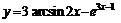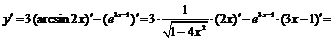
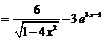Задание 5

Задачи 81–100.Найти производные заданных функций.

81.	;	;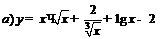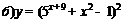
	;	.
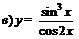82.	;	;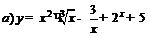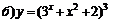
	;	.
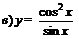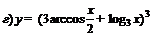83.	;	;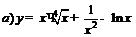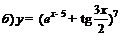
	;	.
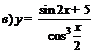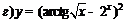84.		;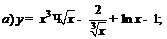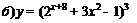
	;	.
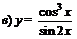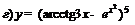85.	;	;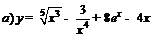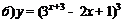
	;	.
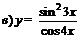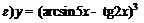86.	;	;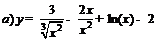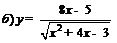
	;	.
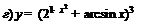87.		;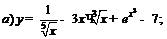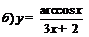
	;	.
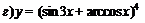88.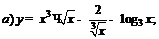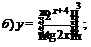
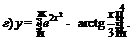89.	;	;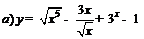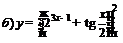
	;	.
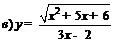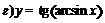90.	;	;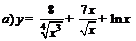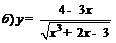
	;	.
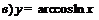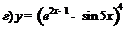91.	;	;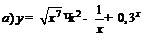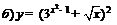
	;	.
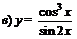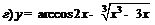92.	;	;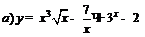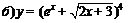
	;	.
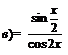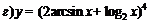93.	;	;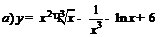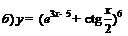
	;	.
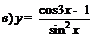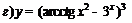94.	;	;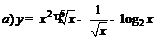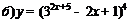
	;	.
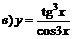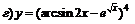95.	;	;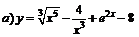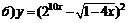
	;	.
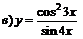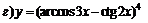96.	;	;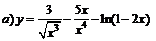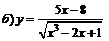
	;	.
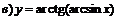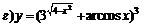97.		;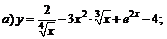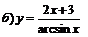
	;	.
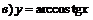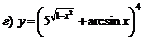98.	;	;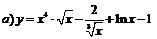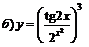
	;	.
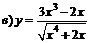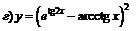99.	;	;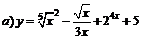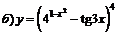
	;	.
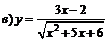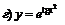100.	;	;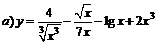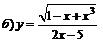
	;	.

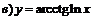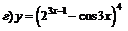Пусть требуется провести полное исследование функции 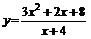и построить ее график.

1. Область определения функции 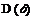характеризуется неравенством х+4¹0, откуда получаем х¹–4, т. е.

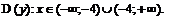
2. Исследуем функцию на непрерывность. Из пункта 1 следует, что функция не определена в точке x= –4. Значит, эта точка является точкой разрыва графика функции. Классифицируем данный разрыв. Для этого вычислим односторонние пределы функции в этой точке:

, .

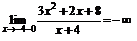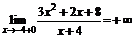Таким образом, точка 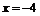является точкой разрыва второго рода, а прямая 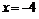– вертикальной асимптотой графика функции.

3. Исследуем функцию на наличие наклонных асимптот:

.

.

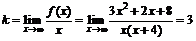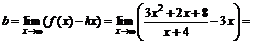
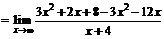
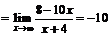Так как оба предела существуют и конечны, то прямая y=3x –10 является наклонной асимптотой графика функции.

4. Функция имеет общий вид, так как область ее определения не симметрична относительно начала координат.

5. Исследуем функцию на экстремум. Для этого найдем критические точки – это точки, в которых первая производная функции обращается в ноль или не существует. Первая производная функции будет равна:

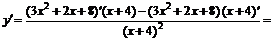
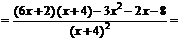
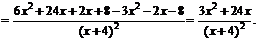
Приравняем ее к нулю: 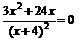. Решим полученное уравнение. Данное уравнение равно нулю, когда числитель равен нулю: 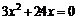. В результате получаем критические точки .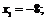

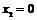Разобьем область определения критическими точками на интервалы и определим знаки первой производной на каждом интервале:

x	(-¥; –8)	–8	(–8; –4)	–4	(–4; 0)		(0; +¥)
y¢	+		–	Не сущ.	–		+
y	Лабораторно-практическое занятие N4. Умножение матриц. Вычисление обратной матрицы. Решение уравнений и систем линейных уравнений Решение систем линейных уравнений методом Гаусса. При решении систем линейных уравнений используют также метод Гаусса (метод последовательного исключения неизвест­ных) Решение систем линейных алгебраических уравнений. Системы линейных алгебраических уравнений можно решать также, используя команду solve Лабораторно-практическое занятие №7. Умножение матриц. Вычисление обратной матрицы. Решение уравнений и систем линейных уравнений Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса Решение систем линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных или основная матрица системы вырожденная, методом Гаусса Решение систем линейных уравнений Решение систем линейных уравнений Решение уравнений и систем линейных уравнений Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса. ← Предыдущая страница | Следующая страница →