Основы сопротивления материалов

2.1 Внутренние силовые факторы. Понятие о напряжениях

2.1.1 Внутренние силовые факторы

Смещение атомов при деформациях материала под действием внешних сил сопровождается изменением, так называемых, внутренних сил взаимодействия между атомами. Эти внутренние силы сопротивляются стремлению внешних сил изменить форму и разрушить тело. Они стремятся восстановить первоначальную форму тела после снятия нагрузок, т.е. освободить тело от упругих деформаций.

Внутренние межатомные силы, возникающие как результат деформации от внешних сил, и являются предметом изучения сопротивления материалов, так как именно их величина характеризует способность тел сопротивляться внешним воздействиям. Эти силы принято называть внутренними силовыми факторами (В.С.Ф.).

Для определения В.С.Ф. пользуются методом сечений.

Допустим, на некоторое тело произвольной формы (например, брус) действует равновесная система внешних сил F₁,F₂ ... F₆, под действием которых тело находится в равновесии.

Выбираем систему координат, причем ось «z» всегда совпадает с осью бруса. Плоскость «zOx» будем считать горизонтальной, «zOy» - вертикальной (рисунок 2.1, а).

Рисунок 2.1

Тело мысленно рассекаем в интересующем нас месте секущей плоскостью W перпендикулярно оси z на части А и В.

Действие частей А на В и В на А заменяют внутренней системой сил в сечении, которые и определяют взаимодействие между частицами рассеченного тела А и В. Внутренние силы по принципу действия и противодействия всегда взаимны, т.е. часть А действует на часть B также, как и часть B на часть А (рисунок 2.1, б).

Внутренние силы распределяются сложным образом по поверхности проведенного сечения и в различных сечениях будут различны.

Так как тело под действием внешних сил находилось в равновесии, то внутренние силы, которые для каждой части являются внешними, должны уравновесить каждую часть А и B.

Таким образом, внутренние силы сводятся к категории внешних сил, и для их определения можно использовать уравнения статики, из которых находят не закон распределения внутренних сил по сечению, а только их равнодействующую, при условии, что все внешние силы заданы.

Воспользовавшись правилами статики, приведем систему внутренних сил части А к центру тяжести сечения (рисунок 2.1, в).

В результате получим главный вектор F и главный момент М. Спроектировав главный вектор и главный момент на оси координат x, y, z, получим шесть составляющих: три силы вдоль осей и три момента относительно этих осей.

Эти составляющие называются В.С.Ф. в сечении бруса. При условии, что внешние силы заданы, В.С.Ф. определяются из шести уравнений равновесия для отсеченных частей бруса:

S F_x= 0; S F_y= 0; S F_z= 0; S М_x= 0; S М_y= 0; S М_z= 0.

В.С.Ф. имеют следующие обозначения и названия:

F_Nz= F_z- продольная сила (растягивающая или сжимающая);

F_Qy= F_y- поперечная сила в вертикальной (zOy) плоскости;

F_Qx= F_x- поперечная сила в горизонтальной (zOx) плоскости;

М_z - крутящий момент;

М_y, М_x - изгибающие моменты в горизонтальной и вертикальной плоскостях.

Этим видам внутренних сил соответствуют следующие виды деформаций:

1) растяжение или сжатие - при появлении в поперечных сечениях только продольных сил F_z;

2) сдвиг - при появлении в поперечных сечениях только поперечных сил F_y, F_x;

3) кручение - в поперечных сечениях возникают только крутящие моменты – М_z;

4) изгиб - в сечениях действует только изгибающий момент М_xили М_y.

Появление в поперечных сечениях сразу нескольких внутренних силовых факторов приводит к сложным видам деформаций.

2.1.2 Напряжения

Эффективной характеристикой для оценки нагруженности деталей или элементов конструкций является интенсивность внутренних сил взаимодействия (напряжений) (рисунок 2.2, а).

В поперечном сечении части А тела выделим элементарную площадку DA, в пределах которой выявлена равнодействующая внутренних сил DF. За среднее напряжение на данной площадке принимают отношение р_cp= DF/DA.

Если площадку DA уменьшать, стягивая ее в точку, то в пределе получим напряжение в точке

р = lim DF/DA = d F/d A [Н/м²(Па); H/мм²(МПа)].

^{DA® 0}

Напряжением в точке называется интенсивность внутренних сил, передающихся в данной точке через единицу площади сечения.

Полное напряжение р (также как и элементарная равнодействующая сила DF) может быть разложено на три составляющие: по нормали к плоскости сечения (ось z) и по двум осям (x, y) в плоскости сечения.

Проекция вектора полного напряжения на нормаль называется нормальным напряжением.

.

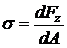Нормальные напряжения стремятся сблизить или удалить отдельные частицы тела по направлению нормали к плоскости сечения (рисунок 2.2, б).

Составляющие в плоскости сечения называются касательными напряжениями. Касательные напряжения стремятся сдвинуть одни частицы тела относительно других по плоскости сечения, поэтому их называют еще напряжениями сдвига.

; .

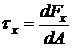Рисунок 2.2

Из рисунка следует:

; ; .

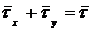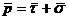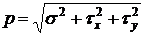Величина напряжения зависит от проведенного сечения (рисунок 2.3).

Для нормального поперечного сечения: р = s = F_z/ A (рисунок 2.3, а);

t_x= t_y= 0.

Для наклонного поперечного сечения: (рисунок 2.3, б);

s_a= р_acosa; t_a= р_asina (рисунок 2.3, б).

Через любую точку можно провести бесчисленное множество сечений (площадок) W_a, по которым в общем случае будут действовать как нормальные, так и касательные напряжения. При этом величины и направления указанных напряжений в каждом конкретном случае будут зависеть от ориентации площадок. Совокупность напряжений для множества площадок образует напряженное состояние в точке. Исследовать напряженное состояние в точке тела - значит получить зависимости, позволяющие определить напряжения по любой площадке, проходящей через данную точку.

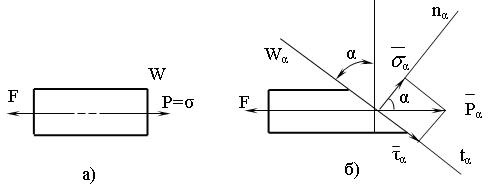
Рисунок 2.3

2.1.3 Основные гипотезы и допущения СМ

В СМ принимают относительно свойств материалов, нагрузок и характера деформации следующие гипотезы и допущения:

1) Гипотеза о сплошном строении тела: материал полностью заполняет объем тела (пустоты отсутствуют).

2) Гипотеза об идеальной упругости материала: тела восстанавливают свою первоначальную форму и размеры после снятия нагрузок.

3) Гипотеза об однородности материала: все частицы материала обладают одинаковыми свойствами.

4) Гипотеза об изотропности материала: свойства материала одинаковы в любом направлении. Для некоторых материалов эта гипотеза неприменима, например, для дерева (колют дрова вдоль волокон).

5) Гипотеза плоских сечений: поперечные сечения, плоские и нормальные к оси тела до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.

6) Допущение о малости деформаций: деформации тела настолько малы по сравнению с его размерами, что не оказывают существенного влияния на взаимное расположение нагрузок.

7) Допущение о линейной зависимости между деформациями и нагрузками: для большинства материалов перемещения, в результате деформации тела, прямо пропорциональны вызвавшим их нагрузкам.

8) Принцип независимости действия сил (принцип суперпозиции или наложения): суммарное воздействие системы сил на деформируемое тело равно сумме воздействия каждой силы в отдельности (справедлив при упругих деформациях).

9) Принцип Сен-Венана: напряжения в сечениях элемента конструкции, достаточно удаленных от мест приложения нагрузки, не зависят от способа нагружения (рисунок 2.4).

Например, при расчете зубчатых колес по напряжениям изгиба можно фактическую нагрузку в зацеплении, распределенную в зоне контакта зубьев по некоторому закону, заменить сосредоточенной силой.

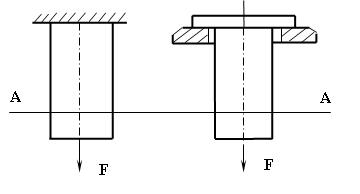
Рисунок 2.4

Принятые гипотезы и допущения широко используются в расчетах элементов конструкций на прочность, жесткость и устойчивость.

2.2 Геометрические характеристики плоских сечений

Прочность и жесткость детали (конструкции), как правило, характеризуются не только размерами сечения, но и его формой. Поэтому к геометрическим характеристикам плоских сечений кроме площади поперечного сечения, относятся статические моменты площади, моменты инерции площади, радиусы инерции, моменты сопротивления площади поперечных сечений.

2.2.1 Основные понятия и определения

Статический момент площади относительно произвольной оси - это сумма произведений элементарных площадок на расстояние их до оси:

; .

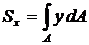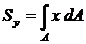Статический момент может быть положительным, отрицательным и равным нулю, измеряется в см³, м³ (рисунок 2.5).

Если для указанной площади поперечного сечения известны координаты центра тяжести С (а и b) относительно произвольных осей x и y, то статические моменты площади относительно этих осей равны произведению площади сечения на расстояние от центра тяжести сечения до данных осей:

S_x = А×а; S_y =А×b.

Оси, проходящие через центр тяжести фигуры, называют центральными осями: x_C и y_C. Статические моменты площади сечений относительно центральных осей равны нулю S_xc= 0, S_yc= 0. Следовательно, если статический момент площади относительно какой-либо оси обращается в ноль, то эта ось проходит через центр тяжести сечения, т.е. является центральной.

Рисунок 2.5

Моменты инерции сечения. Различают осевые, полярные и центробежные. Осевым моментом инерции площади сечения относительно какой-либо оси называется сумма произведений элементарных площадок на квадраты расстояний их до этой оси:

, всегда больше нуля.

Полярным моментом инерции площади сечения относительно полюса O называется сумма произведений элементарных площадок на квадраты расстояний от них до этого полюса:

, всегда больше нуля.

Центробежным моментом инерции сечения относительно двух взаимно-перпендикулярных осей называется сумма произведений элементарных площадок на их расстояние до этих осей, т.е. их координаты:

.

Может быть положительным, отрицательным и равным нулю. Моменты инерции измеряются в cм⁴ или м⁴.

Две взаимно-перпендикулярные оси, относительно которых центробежный момент инерции сечения равен нулю, называются главными. Ось симметрии для данной фигуры является главной осью. Если главные оси проходят через центр тяжести, то они называются главными центральными осями и обозначаются U и V.

J_UV= 0.

Осевые моменты инерции относительно главных осей J_U(xc)и J_V(yc)имеют наибольшие и наименьшие значения из всех возможных и называются главными моментами инерции.