Л)-теорема Крамера (с доказательством)

1. Если определительD=detA матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x₁ , x₂ , ..., x_n, определяемое формулами Крамера

2.

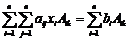
3. Видно, что k это определитель, получающийся из заменой столбца с номером k столбцом свободных членов.

4. X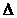_k = _k / 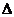, k=1,2, ..., n. – Формула Крамера

Если определитель 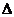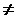0 и система совместна, то она имеет единственное решение, находящиеся по формуле Крамера.

М)-алгоритмы

Алгоритм основан на след.фактах и понятиях:

1) на понятии элементарного преобразования СЛАУ

2) на теореме о том, что всякое элементарное преобразование переводит исходное СЛАУ к новой СЛАУ эквивалентной (равносильной) системе.

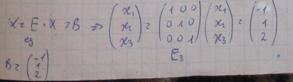
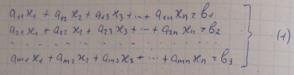
Алгоритм:

Не нарушая общности будем считать, что:

· Неизвестные x1 входит в 1-ре ур. сис. (по существу), т.е с ненулевым коэфицентом (а11ǂ0). Счиатя это предположение выполненным: исключаем неизвестное x1 из всех уравнений системы, кроме 1-ого.

· Неизвестное x1 из 2-ого уравнения:

Первое уравнение умножаем 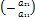и результат прибавляем по 2-ому =˃

Пояснение: неизвестное х1исключено из всех, кроме 1-ого уравнения системы. При этом число уравнений может уменьшится или остаться неизменным.

г) Повторение 1-ого шага, но в системе:

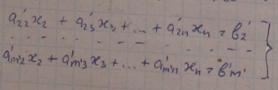
Оказывается при этом, в результате применения метода Гауса, возможны 3 исхода, к которым приводит этот метод:

1) заключается в том, что на каком-то шаге получается уравнение вида 0=b (≠0) - нет решений.

2) Матрица системы приводится к треугольному виду (к верхтреугольному) к такому, что на главной диагонали нет нулей. В этом случае получается единственное решение.

3)матрица системы приводится к виду трапеции

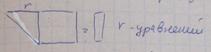
В этом случае системы имеет бесконечное число решений (множество решений)

Н)-определители малого порядка

Существует очень важная характеристика квадратичной матрицы - определитель(детерминант)

Определитель квадратичной матрицы порядка n - это число, которое по некоторому правилу ставится в соответствие каждой квадратной матрице (функция матрицы)

Определитель малых порядков т.е порядка n, для n=1,2,3

1) n=1 - определитель матрицы первого порядка.

2) Второго порядка: А= 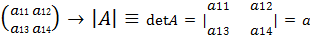11 22- 12 21

О)-Виды матриц

Квадратная - n-го порядка называется матрица размера n×n.

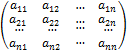
Прямоугольная- матрица размера mxn.

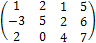
Диагональная (Квадратно-диагональная)-квадратная матрица, у которой все элементы вне главной диагонали равны нулю.

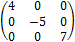
Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали.

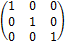
Нулевой называется матрица, все элементы которой равны нулю.

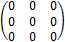
Скалярная - a ∙ E_n

П)-действия над матрицами

Сложение матриц. (Можно складывать матрицы одного и того же размера. Для сложения нужно сложить элементы стоящие на одних и тех же местах.)

Умножение матриц на число. (Можно умножить на любое число.Для этого нужно умножить каждый элемент на число.)

Умножение матрицы на матрицу(можно складывать любые две матрицы одинаковых размеров)

нужно чтобы совпадало число столбцов1-й матрицы и строк 2-й. Произведением матрицыА_m×n на матрицуВ_n×p, называется матрицаС_m×p такая, что
с_ik = a_i1 × b_1k + a_i2 × b_2k + ... + a_in × b_nk,
т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В.