Формула полной вероятности. Ф-ла Байеса.
ДСВ
СВ- переменная величина, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений, причем заранее неизвестно, какое именно.СВ наз-ся ДСВ,если множ-во {х1,х2,…хn}ее возможных значений конечно или счетно (т.е. если все ее значения можно занумеровать).
З-н распр-я СВ - всякое соотношение, устанавливающее связь между возможными значениями СВ и веро-ями, с кот. она принимает эти значения. Обычно его записывают в виде таблицы (ряд распр-я):
| хi | x1 | x2 | … | xn | … |
| pi | p1 | p2 | … | pn | … |
Заметим, что события X=x1,X=x2,…X=хn образуют полную группу,след-но сумма вероятностей этих событий равна 1.

Графически изображ-ся в виде полигона(множ-ва точек на декартовой плос-ти с координатами)или многоуг-ка распред-я(ломаной,соед-щей на полигоне все соседние точки,кроме 1-ой и последней).
НСВ
СВ- переменная величина, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений, причем заранее неизвестно, какое именно.СВ называется НСВ, если ее фун-я распр-я непрерывна на всей числ. оси и дифференцируема кроме,м.б., конечного числа точек. Из этого определения следует P(x1≤X≤x2)= P(x1<X≤x2)= P(x1≤X< x2)= P(x1< X<x2).
Ф-ция распределения вероятностей
Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что CB Х примет знач-е < х:
F(x)=P(X<x).

Cв-ва:1)0≤F(x)≤1.
2)F(x2)≥F(x1).
3)F(x)в точке x0 непрерывна слева 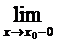 =F(x0).
=F(x0).
4)limF(x)(x→-∞)=0 и limF(x)(x→+∞)=1.
5)P(X=x0)=F(x0+0)-F(x0-0)=F(x0+0)-F(x0).
6)P(a≤X<b)=F(b)-F(a).
14.Плотность распределения вероятностей:
р(х)= 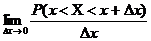
Функция р(х) называется плотностью распределения вероятностей. График функции р(х) называется кривой распределения.
Свойства ПРВ:
1) F(x)=P(X<x)= 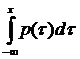 ,т.е сущ-ет так называемая интегральная связь между функциями р(х) и F(х). Функцию F(х) иногда называют интегральной
,т.е сущ-ет так называемая интегральная связь между функциями р(х) и F(х). Функцию F(х) иногда называют интегральной
функцией распределения или интегральным законом распределения.
2. Следовательно, если функция р(х) непрерывна в точке x , то функция
распределения F(х) дифференцируема в этой точке, причем
р(х)=F’(х), т.е. сущ-ет так называемая дифференциальная связь
между функциями р(х) и F(х) . Следует отметить, что плотность распределения
р(х) называют также дифференциальной функцией распределения.
3. т.к. F(x)-неубыв ф-ция, р(х)>или= при всех х.
4. 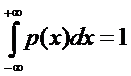
МО СВ
Мат.ожиданием ДСВ называется сумма произведений ее возможных значений на соответствующие им вероятности:
М(Х)=х1р1+х2р2+…хnрn= 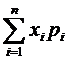 .
.
Св-ва: 1)а≤М(Х)≤b.
2)M(C)=C.
3)M(CX)=CM(X).
4)M(XY)=M(X)*M(Y).
5)M(X+Y)=M(X)+M(Y)
Мат.ожиданиемHСВ:
M(X)= 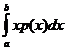
Если значения НСВ Х принадлежат бесконечному интервалу (- 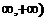 , то ее
, то ее
математическое ожидание определяется формулой
М(Х)= 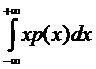 .
.
Свойства те же, что и для ДСВ.
Разность Х-М(Х) наз-ся отклонением СВ Х от её М(Х). Отклонение является случайной
величиной. Покажем, что математическое ожидание отклонения равно нулю.
Действительно, М(Х-М(Х))=М(Х)-М(М(Х))=М(Х)-М(Х)=0
Это равенство объясняется тем, что отклонения могут быть как положительными, так и отрицательными; в результате их взаимного погашения среднее значение отклонения равно нулю.
16.Дисперсия СВ– мат. ожидание квадрата ее отклонения от мат. ожидания:
D(X)=M(X-M(X))2=M(X2)-M2(X).
Св-ва:1) дисперсия постоянной величины С равна нулю:
D(C)=0;
2) Постоянный множи
3)
4) тель можно выносить за знак дисперсии, возведя его в квадрат:
D(CX)=C2D(X);
3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
D(X+Y)=D(X)+D(Y)
4) Дисперсия разности двух независимых случайных величин равна сумме
их дисперсий:
D(X – Y) = D(X) + D(Y).
Ср.квадратич.отклон-ем σ СВ Х наз-ся квадратный корень из дисперсии:σ=кореньD(X)
18.БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЕГО ХАР-КИ!!
Ряд распределения бином з-на имеет вид:
| xi | … | m | … | n | |||
| pi | q 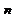 | C 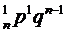 | C 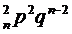 | … | C 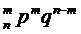 | … | p 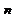 |
Т-ма: Мат. ожидание и дисперсия СВХ,распределенной по биномиальному закону, вычисляются соответственно по ф-лам:
M(X)=np; D(X)=npq;
Док-во:
Доказательство. СВ Х–число наступлений события А в n независимых испытаниях–можно представить в виде суммы n независимых величин Х=Х1+Х2+…+Хn= 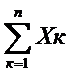 , каждая из которых имеет один и тот же з-н распределения:
, каждая из которых имеет один и тот же з-н распределения:
| xi | ||
| pi | q | p |
СВ Хк, которую называют индикатором события А, выражает число наступлений события A в k-м испытании k=1,2,…,n , т.е. при наступлении события A Xk=1 с вероятностью p, при ненаступлении A Xk=0 c вер-стью q.
Найдем числовые характеристики индикатора события A:
M(X)=x1p1+x2p2=1*p+0*q=p
D(X 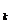 )=x
)=x 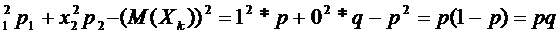
Таким образом, математическое ожидание и дисперсия рассматриваемой СВ X:
М(Х)=М(Х1+Х2+…+Хn)=р+р+…+р=np
D(X)=D(X1+X2+…+Xn)=pq+pq+…+pq=npq.
Распределение Пуассона
Рассмотрим дискретную случайную величину Х, принимающую только целые неотрицательные значения (0, 1, 2,…, m,…), последовательность которых бесконечна, но счетна. Такая случайная величина называется распределенной по закону Пуассона, если вероятность того, что она примет значение m,выражается формулой Пуассона:
P(X=m)= 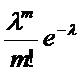
Где λ-параметр закона Пуассона(положит величина) .
| xi | … | m | … | |||
| pi | e 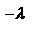 | 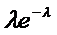 | 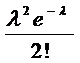 | … | 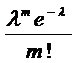 | … |
Очевидно, что определение закона Пуассона корректно, так как основное
свойство ряда распределения выполнено, ибо сумма всех вероятностей
равна 1:
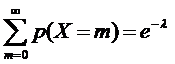 +
+ 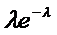 +
+ 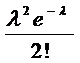 +
+ 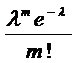 +…=
+…=
=e 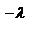
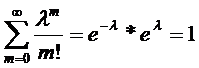
Мат.ожидание и дисперсия СВ Х,распределенной по закону Пуассона, вычисляются соответственно по формулам:
M(X)= λ;D(X)=λ;
Т-ма: Сумма двух независимых СВ, подчиняющихся распр-ю Пуассона с параметрами λ1 и λ2, также имеет распределение Пуассона с параметром λ1+λ2.
Нормальный ЗР
НСВ Х имеет нормальный закон распределения (закон Гаусса) с параметрами а иσ2, если ее плотность вероятности имеет вид:
р(х)=  при -∞<х<+∞;
при -∞<х<+∞;
x=a
|
 p(a)=
p(a)= 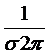
ФР для норм з-на имеет вид:
F(x)= 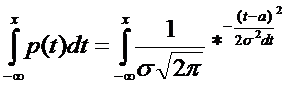
ФР для норм з-на выражают через ф-цию Лапласа:
F(x)= 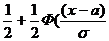
Вероятность попадания норм-но распределённой СВ Х в интервал от 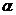 до
до 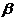 :
:
Р( 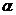 <Х<
<Х< 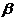 )=F(
)=F( 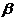 )-F(
)-F( 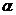 )=
)=
= 
М(Х)=а; D(X)=σ2;
25.(теорема Чебышева). Если Х1, Х2,…, Хn – попарно независимые случайные величины, дисперсии которых ограничены одной и той же постоянной, т.е. D(Xi) ≤ C, то при неограниченном увеличении числа n и для сколь угодно малого числа ε имеет место равенство:

Формула полной вероятности. Ф-ла Байеса.
Следствием двух основных теорем теории вероятностей-теоремы сложения и умножения – являются формулы полной вероятности и формулы Байеса. На языке алгебры событий наборН1,Н2,…Нn называется полной группой событий, если:1) HiHj=∅;…∀i≠j;…i=1,2,…n;j=1,2,…n.2)H1+H2+…+Hn=Ω.
Ф-ла Полн Вер-сти: если событие А м. произойти только при усл-ии появления 1 из событий Нi,где i=1,2,…n,образ-щих полную группу,то вер-ть=:
Р(А)=Σ(от i=1 до н)Р(Нi)*Р 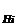 (А).
(А).
Докво:
А=ΩА=А*(Н1+H2+…+Hn)=Н1*А+H2*А+…+Hn*А=>Р(А)=Р(Н1*А+H2*А+…+Hn*А)=Σ(от i=1 до n)Р(НiА).=> Р(А)=Р(Н1)*Р 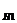 (А)+Р(Н2)*Р
(А)+Р(Н2)*Р 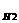 (А)+…+Р(Нn)*Р
(А)+…+Р(Нn)*Р  (А)=Σ(от n до i=1)Р(Нi)*РНi(А).ФБ:если событие А произошло,то апостериорные усл.вер-ти гипотез Н1…Нnвычисл-ся по ф-лам:РА(Нi)=(Р(Нi)*РНi(А))\Σ(от n до i=1)Р(Нi)*РНi(А).Док-во:А*Нi=Нi*А=>P(А*Нi)=P(Нi*А) =>РА(Нi)=(Р(Нi)*РНi(А))\P(A)=>P(A)=Σ(от i=1 до n )Р(Нi)*Р
(А)=Σ(от n до i=1)Р(Нi)*РНi(А).ФБ:если событие А произошло,то апостериорные усл.вер-ти гипотез Н1…Нnвычисл-ся по ф-лам:РА(Нi)=(Р(Нi)*РНi(А))\Σ(от n до i=1)Р(Нi)*РНi(А).Док-во:А*Нi=Нi*А=>P(А*Нi)=P(Нi*А) =>РА(Нi)=(Р(Нi)*РНi(А))\P(A)=>P(A)=Σ(от i=1 до n )Р(Нi)*Р  (А).
(А).
ФОРМУЛА БАЙЕСА:
Если событие А произошло, то апостериорные условные вероятности гипотез Hi, (i=не (1,n))вычисляются по формуле, которая носит название формулы Байеса:
Pa(Hi)= 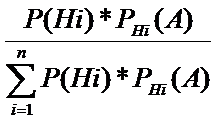
8. Ф-ла Бернулли.
Если вероятность p наступления события A в каждом испытании постоянна, то вер-ть Pn(m) того, что соб-е A наступит ровно m раз в n незав-ых исп-ях выч-ся по ф-ле,наз-ой ф-oй Бернулли:
Pn(m)=C 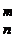 *pm*qn-m.
*pm*qn-m.
Доказательство. Пусть Аi и неA i– соответственно появление и непоявление события A в i-м испытании ( i=1, 2, …n), а B  – событие, состоящее в том, что в n независимых испытаниях событие А появилось m раз. Представим событие B
– событие, состоящее в том, что в n независимых испытаниях событие А появилось m раз. Представим событие B  через элементарные события Ai. Например, при n=3 и m=2 соб-2 B2=A1A2неА3+А1неА2А3+неА1А2А3.
через элементарные события Ai. Например, при n=3 и m=2 соб-2 B2=A1A2неА3+А1неА2А3+неА1А2А3.
В общем виде B  =А1А2…А
=А1А2…А  неА
неА 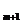 …неА
…неА  + А1неА2А3… А
+ А1неА2А3… А  неА
неА 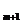 …неА
…неА 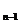 +…+неА1неА2…неА
+…+неА1неА2…неА  А
А  …An, (1)
…An, (1)
т.е. каждый вариант появления события (каждый член суммы (1)) состоит из m событий
A и n-m событий неA с различными индексами. Число всех комбинаций (слагаемых суммы (1)) равно числу способов выбора из n испытаний m, в которых событие A произошло, т.е. числу сочетаний C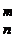 .
.
Вероятность каждой такой комбинации по теореме умножения для независимых событий равна pm*qn-m . В связи с тем, что комбинации между собой несовместны, то по теореме сложения вероятностей получим
Pn(m)=P(Bm)=pm*qn-m+…+ pm*qn-m=C 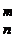 *pm*qn-m
*pm*qn-m

9.Ф-ла Пуассона:если р наступления события А в каждом испыт-ии стремится к 0((р→0), р<0,1) при неогранич-м увел-ии числа n испытаний(n→∞,n≥100),причем произв-е np стрем-ся к пост числу λ (np→λ) (пост.число,λ≤10),то вер-ть Pn(m) того, что соб-е А появится m раз в n испытаниях, удовлетворяет предельному равенству:
 Pn(m)=(λme-λ)/m!
Pn(m)=(λme-λ)/m!
Если в схеме Бернулли вероятность p появления события A близка к 1, а число испытаний n велико, для вычисления вероятности Pn(m)также можно использовать формулуПуассона.При этом находят вероятность того,что событие нeA произойдет n-m раз.
10. Локальная теорема Лапласа:
если в схеме Бернулли вероятность p появления события A в каждом из n испытаний существенно отличается от 0 и 1(0,1≤p≤0,9),то вер-ть Pn(m) того, что соб-е А произойдёт m раз в n независ испытаниях при достаточно большом числе n (n>100) приближённо равна:
Рn(m)  ,где фи(х)=
,где фи(х)= 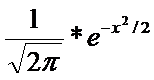 - ф-ция Гаусса, х=
- ф-ция Гаусса, х= 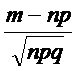
Интегральная теорема Лапласа:
если вероятность p наступления события А в каждом из n независимых испытаний постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что число m наступления события А в n испытаниях заключено между m1 и m2 включительно при достаточно большом числе n приближенно равна
Рn(m1≤m≤m2)  ,
,
Где р-вероятность появления успеха в каждом испытании, q=1-p,
Ф(х)= 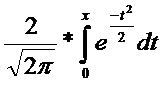 - ф-ция Лапласа.
- ф-ция Лапласа.
ДСВ
СВ- переменная величина, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений, причем заранее неизвестно, какое именно.СВ наз-ся ДСВ,если множ-во {х1,х2,…хn}ее возможных значений конечно или счетно (т.е. если все ее значения можно занумеровать).
З-н распр-я СВ - всякое соотношение, устанавливающее связь между возможными значениями СВ и веро-ями, с кот. она принимает эти значения. Обычно его записывают в виде таблицы (ряд распр-я):
| хi | x1 | x2 | … | xn | … |
| pi | p1 | p2 | … | pn | … |
Заметим, что события X=x1,X=x2,…X=хn образуют полную группу,след-но сумма вероятностей этих событий равна 1.

Графически изображ-ся в виде полигона(множ-ва точек на декартовой плос-ти с координатами)или многоуг-ка распред-я(ломаной,соед-щей на полигоне все соседние точки,кроме 1-ой и последней).
НСВ
СВ- переменная величина, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений, причем заранее неизвестно, какое именно.СВ называется НСВ, если ее фун-я распр-я непрерывна на всей числ. оси и дифференцируема кроме,м.б., конечного числа точек. Из этого определения следует P(x1≤X≤x2)= P(x1<X≤x2)= P(x1≤X< x2)= P(x1< X<x2).
