Испытания по схеме Бернулли.
Так называется следующая серия независимых испытаний. Пусть производится n испытаний. В i-том испытании может осуществиться случайное событие Ai с вероятностью Рi,i=1,…,n. Все события Аi независимы в совокупности. То есть вероятность события Аi не зависит от того, осуществляются или нет события Аj,j=1,…,n, j 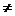 i. Рассмотрим здесь такой частный случай, когда все вероятности Рi равны друг другу и равны p,0‹p‹1. То есть
i. Рассмотрим здесь такой частный случай, когда все вероятности Рi равны друг другу и равны p,0‹p‹1. То есть
Р(Аi)=p, P(Ai*)=q, q=1-p, 0‹p‹1, 0‹q‹1, i=1,…,n
Например, пусть испытания состоят в том, что случайная точка 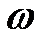 в i-том испытании обязательно появляется в квадрате со стороной равной единице. Событие Аi состоит в том, что точка
в i-том испытании обязательно появляется в квадрате со стороной равной единице. Событие Аi состоит в том, что точка 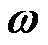 оказывается в четверти круга, вписанного в квадрат и имеющего радиус равный единице. Согласно (7.2) имеем
оказывается в четверти круга, вписанного в квадрат и имеющего радиус равный единице. Согласно (7.2) имеем
Р(Ai)=p= 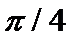 (13.2)
(13.2)
Справедливо следующее утверждение.
Теорема Бернулли: Пусть производится n испытаний по схеме Бернулли. Пусть события Аi осуществились в m испытаниях.
Для любых чисел 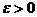 и
и 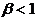 найдется такое натуральное число N, что при числе испытаний n>N будетсправедливо неравенство
найдется такое натуральное число N, что при числе испытаний n>N будетсправедливо неравенство
P(|m/n–p|< 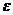 )>
)> 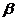 (13.3)
(13.3)
В самом деле, свяжем с i-тым испытанием случайную величину 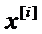 . Пусть эта величина принимает значение равное единице, если осуществляется событие Аi, и
. Пусть эта величина принимает значение равное единице, если осуществляется событие Аi, и 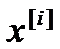 принимает значение равное нулю, если событие Аi не осуществляется, т.е. осуществляется противоположное событие Аi*. Вычислим математическое ожидание Еi и дисперсию Di случайной величины
принимает значение равное нулю, если событие Аi не осуществляется, т.е. осуществляется противоположное событие Аi*. Вычислим математическое ожидание Еi и дисперсию Di случайной величины 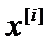 . Имеем
. Имеем
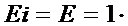 p
p 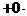 q=p(13.4)
q=p(13.4)
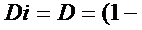 p
p 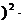 p
p 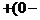 p
p 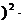 q
q 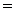 q
q 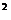 ∙p+p
∙p+p 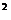 ∙q=p∙q∙(q+p)=p∙q∙1=p∙q(13.5)
∙q=p∙q∙(q+p)=p∙q∙1=p∙q(13.5)
Так как в нашем случае
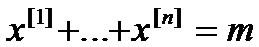 (13.6)
(13.6)
то из закона больших чисел (12.9),(12.10) получаем неравенство (13.3), если только
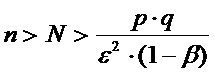 (13.7)
(13.7)
Это и доказывает теорему Бернулли.
Например, если мы хотим проверить теорему Бернулли на примере вычисления числа р с точностью до 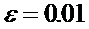 с вероятностью большей, чем
с вероятностью большей, чем 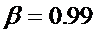 , то нам надо сделать испытания по схеме Бернулли в соответствии с разделом 7, т.е. получить согласно текущему разделу неравенство
, то нам надо сделать испытания по схеме Бернулли в соответствии с разделом 7, т.е. получить согласно текущему разделу неравенство
P(|m/n–р/4|<0.01)>0.99 (13.8)
Для этого согласно (13.7) достаточно выбрать число
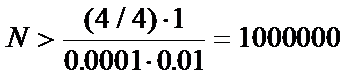 (13.9)
(13.9)
с большим запасом.
Такое испытание было сделано на компьютере по программе, приведенной в следующем разделе. Получилось
4∙m/n=3.1424 (13.10)
Мы знаем, что число р=3.1415925626…. То есть действительно получилось число с точностью по крайней мере до 0.01.
Метод Монте-Карло.
Испытания по схеме Бернулли составляют основу вычислительного метода, который предложил Фон-Нейман для расчета сложных процессов. Например, для расчетов при создании атомной бомбы. Этот метод он назвал методом Монте-Карло в честь города, в котором идет игра в рулетку. Суть этого метода состоит в том, что подбираются такие испытания по схеме Бернулли, в которых вероятности событий Аi и определяют интересующую вычислителя величину. Простейший пример вычисления по методу Монте-Карло и приведен в разделах 13,14 для числа р. Особенно удобно вычислять методом Монте-Карло площади и объемы сложных фигур и тел.
Теоремы сложения.
Теорема 1. Пусть А и В – два несовместных события. Тогда вероятность того, что осуществится хотя бы одно из этих двух событий, равна сумме их вероятностей: P(A U B)=P(A)+P(B).
Доказательство.
Обозначим исходы, благоприятные для события А, через а1,а2,…,аm, а для события В – через b1,b2,…,bn. Вероятности этих исходов обозначим соответственно через p1,p2,…,pmиq1,q2,…,qn . Тогда событию A UBблагоприятны все исходы a1,a2,…,am , b1,b2,…,bn. В силу того что события А и В несовместны, среди этих исходов нет повторяющихся. Поэтому вероятность событияАUB равна сумме вероятностей этих исходов. т.е.
P(AUB)=p1+p2+…+pm+q1+q2+…+qn.
Но p1+p2+pm=P(A), q1+q2+qn=P(B), а потому
P(AUB)=P(A)+P(B). Теорема доказана.
Испытанием называется реализация определенного комплекса условий, который может воспроизводиться неограниченное число раз. При этом комплекс условий включает в себя случайные факторы, реализация которого в каждом испытании приводит к неоднозначности исхода испытания.
Например: испытание - подбрасывание монеты.
Результатом испытания является событие. Событие бывает:
Достоверное (всегда происходит в результате испытания);
Невозможное (никогда не происходит);
Случайное (может произойти или не произойти в результате испытания).
Например: При подбрасывании кубика невозможное событие - кубик станет на ребро, случайное событие - выпадение какой либо грани.
Конкретный результат испытания называется элементарным событием.
В результате испытания происходят только элементарные события.
Совокупность всех возможных, различных, конкретных исходов испытаний называется пространством элементарных событий.
Например: Испытание - подбрасывание шестигранного кубика. Элементарное событие - выпадение грани с “1” или “2”.
Совокупность элементарных событий это пространство элементарных событий.
Сложным событием называется произвольное подмножество пространства элементарных событий.
Сложное событие в результате испытания наступает тогда и только тогда, когда в результате испытаний произошло элементарное событие, принадлежащее сложному.
Таким образом, если в результате испытания может произойти только одно элементарное событие, то в результате испытания происходят все сложные события, в состав которых входят эти элементарные.
Например: испытание - подбрасывание кубика. Элементарное событие - выпадение грани с номером “1”. Сложное событие - выпадение нечетной грани.
Введем следующие обозначения:
А - событие;
w - элементы пространства W;
W - пространство элементарных событий;
U - пространство элементарных событий как достоверное событие;
V - невозможное событие.
Иногда для удобства элементарные события будем обозначать Ei, Qi.
Операции над событиями.
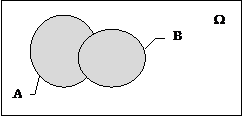
1. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. При этом если элементарное событие входит и в A, и в B, то в C оно входит один раз. В результате испытания событие C происходит тогда, когда произошло событие, которое входит или в A или в B. Сумма произвольного количества событий состоит из всех элементарных событий, которые входят в одно из Ai, i=1, ..., m.
 |
2. Событие C произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B. Произведением произвольного числа событий называется событие состоящее из элементарных событий, входящих во все Ai, i=1, ..., m.

3. Разностью событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.

4. Событие называется противоположным событию A, если оно удовлетворяет двум свойствам.
Формулы де Моргана: 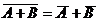 и
и 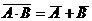
 |
5. События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания.
События A и B называются несовместными, если они не имеют общих элементарных событий.
C=A×B=V
Тут V - пустое множество.
