Функция распред-я и плотность распред-я

Непрерывн-ю СВ нельзя охарактер-ть перечнем её знач-ий и их вероят-тей. Для этого нужна ф-я распред-я, годная и для дискретных,и для непрерывн.СВ

Функц-я распред-я F(x) случайн.величины Х называется вероят-ть того, что случайн.величина примет знач-е, меньшее х: F(x) = F (x) = P(Х< x) (содержит всю информ-ю о случайн.величине) F(x) определена на всей числовой прямой R;  F(x) не убывает, т.е. если x1 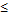x2, то F(x1) 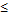F(x2);

Числовые характер-ки ДСВ

Мат.ожидание - сумма произведений всех возможн.значений случайн.величины на их вероятности.(для усредненной оценки нек.случайн.значения).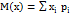

Св-ва мат.ожид-я: 1)Мат. ожид-е по­стоянной величины=самой постоянной: М(С) = С; 2)Постоянный множитель можно выно­сить за знак мат.ожидания: М(СХ) = СМ(Х). 3)Мат.ожид-е произведе­ния 2х независим. СВ = произведе­нию мат.ожиданий сомножителей M(XY) = M(X)·M(Y). 4)Мат.ожидание суммы (разности) 2х СВ = сумме(разности) их мат.ожиданий слагаемых. M(X 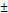Y) = M(X) 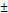M(Y); Мат. Ожидание числа появления события в независимых испытаниях.Мат.ожидание М(Х) числа появления соб.А в n независим.испытаниях=произвед-ю числа испытаний на вероят-ть появления события в кажд. испытании.:M(X)= np . Дисперсия -степень разброса значений случ.величины относит-но её мат.ожидания. D(x) = M(x2) – (M(x))

Св-ва дисперсии 1.Дисперсия постоян.величины равна 0: D (С)=0; 2.Постоян. множитель можно выно­сить за знак дисперсии, возводя его в квадрат: D(CX)-C2 ·D(X).3.Дисперсия суммы 2х независим. СВ = сумме дисперсий этих величин: D (X + Y) = D (X) + D (У) 4. Дисперсия разности 2х независим. СВ = сумме их дисперсий: D (X – Y) = D (X) + D (У).

Дисперсия числа появлений события в независим.испытаниях:Пусть производится п независим. испытаний, в каждом из кот. вероят-ть появления события А постоянна и равна p.Тогда дисперсия числа появлений со­бытия в этих испытаниях вычисл-ся по фор-ле: D(Х)=npq, n–число испыт-ий, p–вероят-ть наступления события, q-вероят-ть не наступления события.

Средн.квадратич-е отклонение-квадратн.корень из дисперсии (когда надо, чтобы оценка рассеяния имела размерность слу­чайн.величины)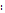

Функц-я распред-я F(x) называется вероят-ть того, что случайн. величина X примет знач-е, меньшее х: F(x) = F (x) = P(Х< x) .

Одинаково распредел-е взаимно независим.СВ Мат.ожидание ср.арифметич-го одинаково распредел.взаимно независ.СВ= мате. ожиданию каждой из этих величин: М( 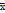)=М. Дисперсия ср.арифметич-го n один-во распредел-х взаимно независим. СВ в n раз меньше дисперсии кажд.из этих величин:D( 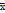)=D/n.Средн. квадратич.отклонение средн.арифметич-го n одинаково распредел-х взаимно независим.СВ в 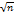раз меньше средн.квадратич. отклонения кажд.из этих величин: ( )= / .

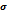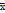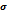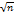1.2.4.Закон больших чисел

Закон больших чиселв теории вероятностейутверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Неравенство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего.

Теорема Чебышёва. Для независимых случайных величин 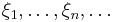соотношение

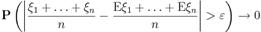
(при любом 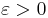и 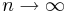) верно при весьма общих предположениях:

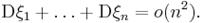
Сущность теоремы Чебышева заключается в том, что хотя каждая из независимых Случ Величин 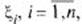может принять значение, далекое от 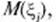среднее арифметическое 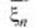при достаточно большом п с большой вероятностью будет весьма близко к 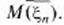Несмотря на то, что отдельные попарно независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа этих величин с большой вероятностью принимает значения, близкие к определенному постоянному числу – среднему арифметическому их математических ожиданий. Другими словами, хотя отдельные случайные величины могут иметь значительный разброс, их среднее арифметическое рассеяно мало. Практическое значение этого факта заключается в том, что можно принять в качестве искомого значения некоторой измеряемой величины среднее арифметическое результатов нескольких измерений.

Теорема Бернулли

Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность P_{k, n} того, что событие A наступит k раз в n независимых испытаиях, равна: 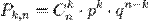где q = 1-p.

Теорема Ляпунова

Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Пусть 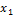, , 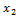…, , …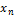- неограниченная последовательность независимых случайных величин с математическими ожиданиями 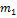, , 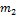…, , … 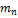и дисперсиями 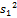, , 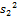…, … 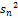. Обозначим , , ,.

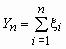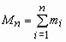
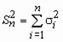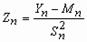Тогда 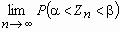= Ф(b) - Ф(a) для любых действительных чисел a и b , где Ф(x) - функция распределения нормального закона.