Численные методы решения систем линейных уравнений (СЛАУ): метод Зейделя.

Метод Зейделяявляется модификацией метода итераций.СЛАУ задается в виде (3.8) и приводится к виду (3.10). Отличие от метода итераций заключается в вычислительной процедуре нахождения приближения на i+1 итерации. В отличии от метода простых итераций , где для отыскания i+1 приближения используется i - ое приближение неизвестных xⁱ_j, в методе Зейделя используются уже вычисленные i+1 значения x . Рекуррентные соотношения используемые в методе Зейделяпредставляются следующим образом:

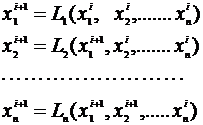(3.12)

Условия сходимости метода Зейделяможет быть сформулировано следующим образом:

Для того чтобы итерационный процесс сходился, достаточно, чтобы сумма абсолютных значений элементов каждой строки (исключая диагональный) была меньше абсолютного значения диагонального элемента соответствующей строки.

Математически это определение может быть выражено следующим образом

На первом этапе решения СЛАУ система приводится к виду (3.10), после чего происходит проверка условия сходимости итерационного процесса к решению системы. Для этого необходимо выбрать максимальные значения коэффициентов a_i,iи провести проверку условия на сходимость итерационного процесса. После этого задаются начальные приближения, обычно для этого используется столбец свободных членов, и проводится расчет по формуле (3.12) до достижения окончательного решения.

Численные методы восстановления функций: постановка задачи.

В вычислительной практике часто приходится иметь дело с функциями 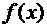, заданными таблицами их значений для некоторого конечного множества значений х: .

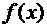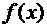В процессе же решения задачи необходимо использовать значения для промежуточных значений аргумента. В этом случае строят функцию Ф(x), достаточно простую для вычислений, которая в заданных точках x₀, x₁,...,x_n, называемых узлами интерполяции, принимает значения , а в остальных точках отрезка (x₀,x_n), принадлежащего области определения , приближенно представляет функцию 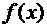с той или иной степенью точности.

При решении задачи в этом случае вместо функции 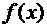оперируют с функцией Ф(x). Задача построения такой функции Ф(x) называется задачей интерполирования. Чаще всего интерполирующую функцию Ф(x) отыскивают в виде алгебраического полинома.

Численные методы восстановления функций: интерполяция полиномом Лагранжа. Интерполяционные формулы Лагранжа и Ньютона.

Для каждой функции 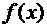, определенной на [a,b], и любого набора узлов x₀, x₁,....,x_n( x_i 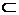[a,b], x_i x_j при i j ) среди алгебраических многочленов степени не выше n существует единственный интерполяционный многочлен Ф(x), который может быть записан в форме:

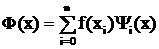, (4.1)

где - многочлен n-ой степени, обладающий следующим свойством:

(4.2)

Для интерполяционного полинома многочлен имеет вид:

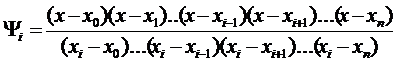(4.3)

Этот многочлен (4.1) и решает задачу интерполирования и называется интерполяционным полиномом Лагранжа.

Пример

В качестве примера рассмотрим функцию вида 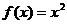на интервале 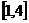заданную табличным способом.

X
F(x)

Необходимо определить значение функции в точке x-2.5. Воспользуемся для этого полином Лагранжа. Исходя из формул (4.1 и 4.3) запишем этот полином в явном виде:

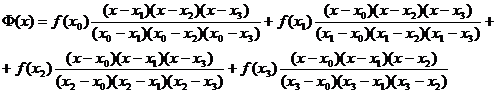(4.4).

Тогда подставляя в формулу (4) исходные значения из нашей таблицы получим

Полученный результат соответствует теории т.е. 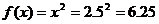.