Численные методы решение алгебраических уравнений: постановка задачи, табличный способ отделения корней.

При этом для многих задач известно только о существовании решения, но не существует конечной формулы, представляющей ее решение. Даже при наличии такой формулы ее использование для получения отдельных значений решения может оказаться неэффективным. Наконец, всегда существует необходимость решать и такие математические задачи, для которых строгие доказательства существования решения на данный момент отсутствуют.

Во всех этих случаях используются методы приближенного, в первую очередь численного решения.

Технологическая цепочка вычислительного эксперимента включает в себя следующие этапы:

1)Построение математической модели исследуемого 2)Построение вычислительного алгоритма - метода приближенного решения поставленной задачи и его обоснование. 3)Программирование алгоритма на ЭВМ и его тестирование. 4)Проведение серии расчетов с варьированием определяющих параметров исходной задачи и алгоритма. 5) Анализ полученных результатов.

Только для простейших уравнений удается найти решение в аналитическом виде, т.е. записать формулу, выражающую искомую величину хв явном виде. В большинстве же случаев приходится решать уравнение вида 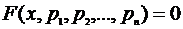численными методами. Хотя иногда, даже при наличии аналитического решения, имеющего сложный вид, бывает проще провести численное решение по известному алгоритму, чем программировать громоздкую аналитическую формулу. На первом этапе необходимо определить интервал изменения переменной х, где расположен один корень или, что означает то же самое, определить достаточно хорошее приближение окрестности этой точки.

На втором этапе тем или иным численным методом определяется величина х, соответствующая корню уравнения (2.1) с заданной погрешностью.

Численные методы решение алгебраических уравнений: метод половинного деления.

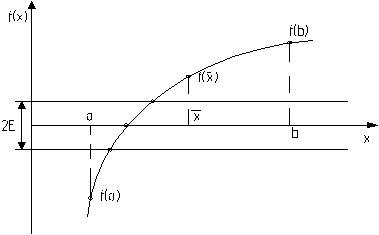
Для применения метода половинного деления необходимо установить окрестность или отрезок[a, b], на котором расположен один из корней уравнения, который необходимо уточнить с погрешностью Е(рис.2.1).

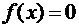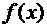Пусть дано уравнение , где непрерывна на отрезке [a, b] и .

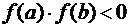Выбираем начальное приближение, равное:

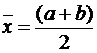
и вычисляем значение функции 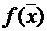. Если 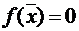, то является корнем уравнения. Если 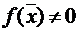, то выбираем, одну из двух частей отрезка 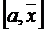или 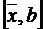для дальнейшего уточнения корня. Естественно, что корень будет находиться в той половине отрезка, на концах которого функция 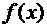имеет разные знаки, а именно проверяем условие: 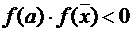. На рис.2.1 это будет отрезок 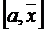, т. е. для очередного шага уточнения точку b перемещаем в середину отрезка 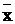(b= 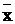) и продолжаем процесс деления как с первоначальным отрезком [a, b].

Процесс деления будет продолжаться до тех пор, пока не будет выполнено условие:

.

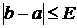За приближенное решение принимается средняя точка последнего промежутка.